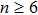† Corresponding author. E-mail:
We perform a theoretical investigation on the control over the atomic excitation of Rydberg states with shaped intense ultrashort laser pulses. By numerically solving the time-dependent Schrödinger equation (TDSE), we systematically study the dependence of the population of the Rydberg states on the π phase step position in the frequency spectra of the laser pulse for different intensities, central wavelengths and pulse durations. Our results show that the Rydberg excitation process can be effectively modulated using shaped intense laser pulses with the laser intensity as high as 1×1014 W/cm2. Our work also have benefit to the future investigation to find out the dominant mechanism behind the excitation of Rydberg states in strong laser fields.
Survival of neutral atoms in (long-lived) Rydberg states in strong laser field has not been paid too much attention in the early time. Only in recent years, both theoretical and experimental works surprisingly found that neutral atoms in Rydberg states can survive very strong laser fields.[1–3] This becomes the subject of elaborate experimental and theoretical studies accompanying new important applications of neutral atoms with high excited states exposed to an oscillating electric field.[4–7] Eichmann et al. identified the ponderomotive force on electrons as the driving mechanism, leading to ultrastrong acceleration of neutral atoms with a very high magnitude.[8] Two theoretical mechanisms have been proposed in order to explain how these excited states are populated and how they remain stable in the intense laser field. In the tunneling regime, the frustrated tunneling ionization (FTI) model successfully describes strong field excitation, which says that the electron does not gain enough drift energy from the laser pulse after tunneling and will eventually be captured by the coulomb field of the ion,[9–13] In the multi-photon regime, the high population of Rydberg states is thought to be resulted from the multiphoton resonance of the ground state and a set of high-lying Rydberg states with AC stack shift, and the interference stabilization (IS) of population trapped in Rydberg states.[14–16] However, there is still no precise and unambiguous theory to explain all the existing phenomena. And whether there exists a effective way to coherently control the strong field Rydberg excitation process is also an interesting question.
On the other hand, the ability to modulate the temporal shape of an ultrashort pulse enables the manipulation of the evolution of a quantum system and thus the control of various atomic and molecular processes. In particular, control of the spectral phase of the pulse and thus its temporal profile has been demonstrated effectively for control over numerous physical systems and processes.[17–20] Corresponding examples of past control studies include the control over multi-photon absorption processes in atoms, over nonresonant two-photon and three-photon absorptions in large molecules, and over molecular Raman transitions.[21–27] And in recent years, there has been increasing interest in the control over the ionization dynamics of atoms and molecules using shaped intense ultrashort laser pulses with the peak intensity higher than 1×1013 W/cm2.[28–31] However, the excitation dynamics of atoms and molecules in shaped intense ultrashort laser pulse is still lack of investigation. Generally, both the ionization and excitation dynamics in strong laser field will be different from the cases in weak field. This is because the atomic potential will be significantly modified by the strong laser electric field, which can not be treated as perturbation any more. In contrast to the multi-photon absorption picture in weak field, electron’s ionization dynamics is governed predominantly by tunneling process in strong laser field. While for excitation process in strong laser field, the mechanism as well as the result of the control will be also not the same as that in weak field.
In this paper, we perform an investigation on the control over the process of Rydberg states excitation in the interaction between the Hydrogen atom with shaped intense ultrashort laser pulse. We test the effect of the coherent control in different laser intensities, center wavelengths, and pulse durations of the shaped intense laser pulses, by numerically solving the time-dependent Schrödinger equation (TDSE). We mainly focus on the potentialities of the scheme for control over the Rydberg excitation using shaped intense laser pulse, and attempt to provide results that would benefit the future work to find out which one of the mechanisms is more suitable to explain the Rydberg excitation process in intense laser fields.
The time-dependent Schröinger equation for atomic hydrogen in intense laser fields can be written as (atomic units 
 |
For a linearly polarized laser pulse, the temporal electric field 
 |

 |
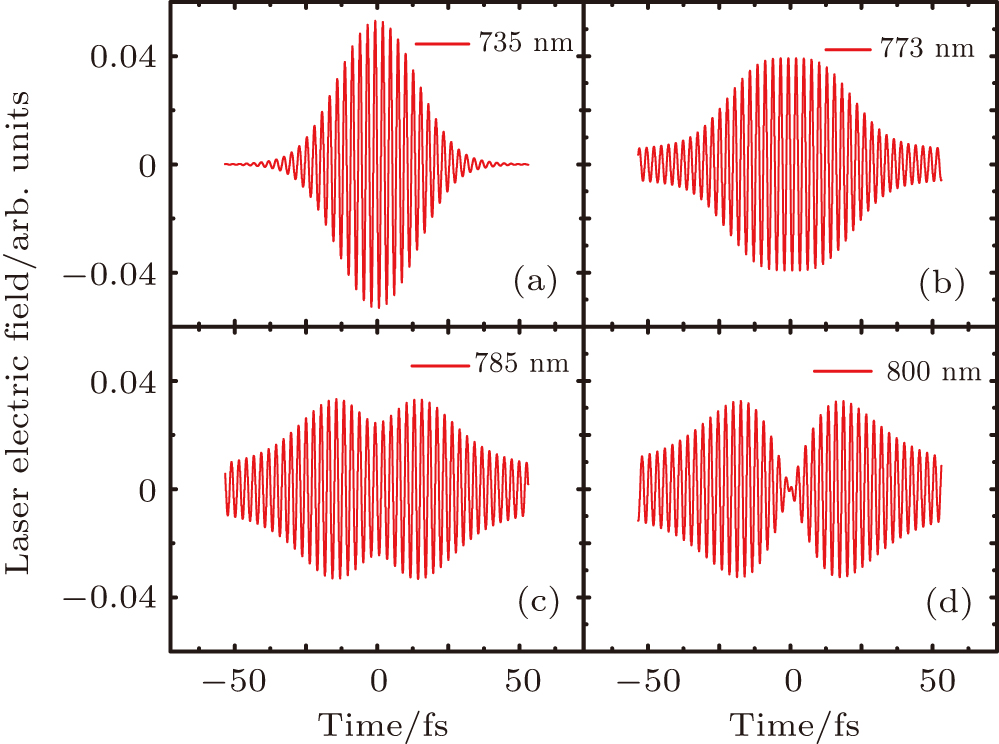
Here the shaped pulse is realized by a simple and intuitive pulse shape parametrization, i.e., a π phase jump in the spectral phase. Experimentally, the pulse shaper is composed of a pair of diffraction gratings, a pair of achromatic lens, and a spatial filter. Briefly, after passing through the first lens and grating, the complex spectrum of the input pulse is spatially mapped at the Fourier plane. A one-dimensional programmable liquid-crystal spatial light-modulator array, composed of many computer-controlled discrete phase elements was placed at the Fourier plane of the shaper, and was used as a dynamic filter which can modify the spectral phase of the pulses. Finally, the second lens and grating reassemble the spectral components to form a modified time-shaped pulse.
Theoretically, we can obtain the shaped pulse in a similar way. We first obtain the unshaped pulse envelope function 
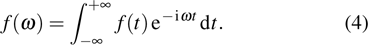 |
 |
In the numerical calculations, the atom is initially in the 1s state, and 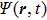
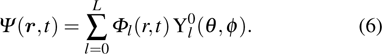 |
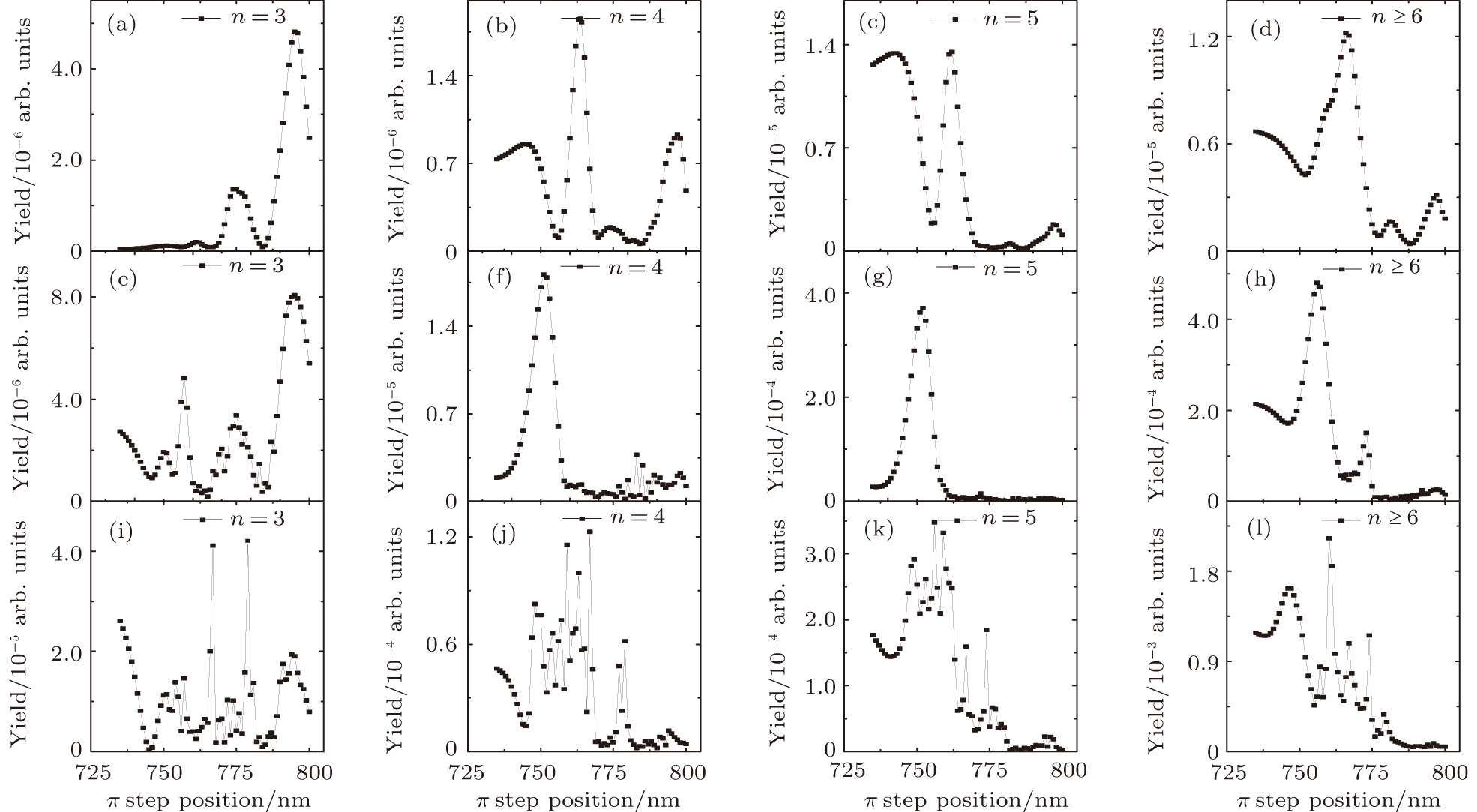
In the following we will show the simulated results for different laser parameters. Figure 
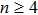
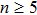
When increasing the laser intensity, the population becomes more and more sensitive on the π step position. At the intensity of I0 (Figs. 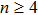
In Fig. 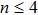

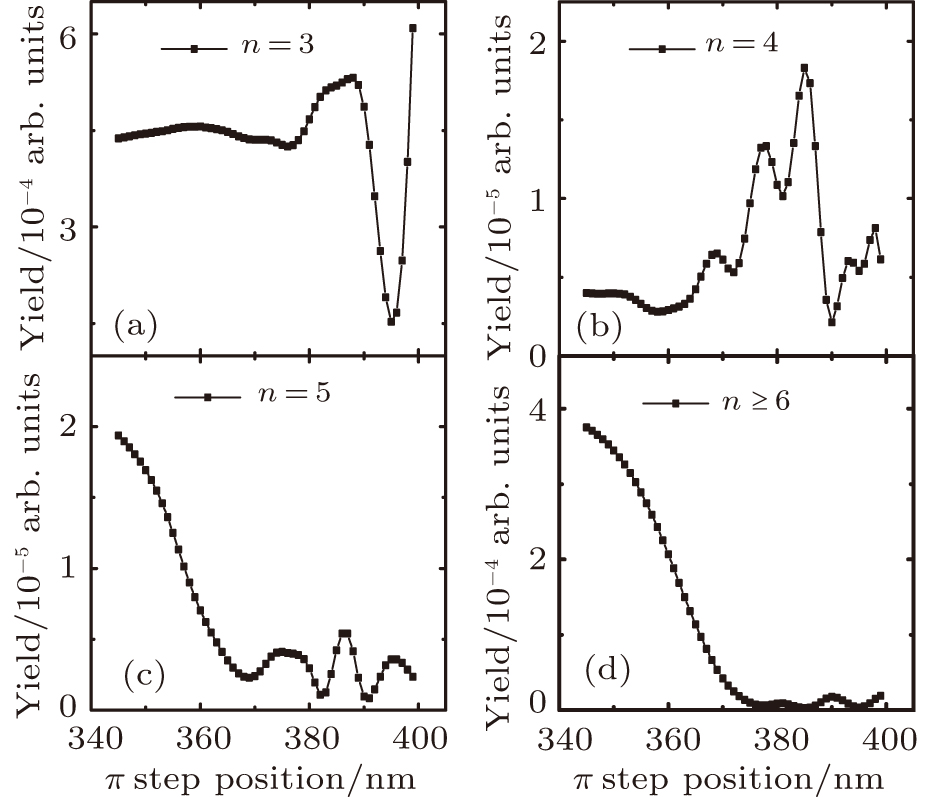 | Fig. 3. Simulation of the n = 3, 4, 5 and 
|
Finally, we calculate the population of different excited states for different pulse durations. In Fig. 
In conclusion, we theoretically verify the availability of coherent control over atomic Rydberg excitation with shaped intense ultrashort laser pulses and investigate its dependence on the laser intensity, central wavelength and pulse duration of the laser pulses. Our results demonstrate that the Rydberg excitation process can be effectively regulated with shaped intense laser pulses only if the laser intensity is not very high. Our work serves as a basis for the future control over the excitation process of Rydberg states and we expect that it can also pave the way towards understanding of the underlying mechanisms of the Rydberg state excitation in intense laser fields.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 |