† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61505261).
Compared with the fiber channel, the atmospheric channel offers the possibility of a broader geographical coverage and more flexible transmission for continuous-variable quantum key distribution (CVQKD). However, the fluctuation of atmospheric conditions will lead to the loss of performance in atmospheric quantum communication. In this paper, we study how temperature affects atmospheric CVQKD. We mainly consider the temperature effects on the transmittance and interruption probability. From the numerical simulation analysis, it can be shown that the performance of atmospheric CVQKD is improved as temperature increases, with the other factors fixed. Moreover, the results in this work can be used to evaluate the feasibility of the experimental implementation of the atmospheric CVQKD protocols.
Quantum key distribution (QKD),[1,2] which allows two legitimate parties to establish a random secret key between them, is probably the most significant branch of quantum communication. The security of QKD is provided by the laws of quantum mechanics. Compared with the discrete-variable quantum key distribution (DVQKD) system,[3] the CVQKD system has the following advantages: first, the preparation of light sources are relatively simple; second, the detectors have low cost and high detection efficiency; and finally, it can be effectively compatible with existing optical communication systems. For these reasons, the CVQKD has received extensive attention and be studied in depth in the area of quantum communication.[4]
The quantum channel is one of essential factors in the QKD systems. The most common channel in implementation is the optical fiber and the free space channel,[5,6] and the latter provides great flexibility in the establishment of infrastructure and in the connection with moving objects.[7,8] However, the negative effects of the free-space channel in atmosphere such as the background light and atmospheric turbulence cannot be ignored.[9] Therefore, it is necessary to establish a comprehensive transmission model and carry out the corresponding performance analysis of QKD in the atmosphere. The model was studied in the recent years.[10–14] An elliptical beam model considering beam wandering, broadening and deformation has been established for quantum light through the atmospheric channel,[15] then others factors, such as arrival time fluctuations and angle-of-arrival fluctuations, were also considered in this model.[16–19] However, in the QKD system, the quantum states in atmospheric channels are sensitive to fluctuation of temperature. When the beam propagates in the turbulent atmosphere, the temperature fluctuation of the turbulent atmosphere causes the refractive index to fluctuate,[20] which leads to a series of turbulence effects such as beam wandering, scintillation, transmission fluctuation, communication interruption, etc. Therefore, the temperature effects should be considered in the atmospheric CVQKD.[21–26]
In this paper, we mainly consider the temperature effects on atmospheric CVQKD, through taking into consideration two parameters that can affect the secret key rate. First, considering the temperature effects on transmittance, our results demonstrate that the temporal pulse broadening decreases with the increase of temperature. Second, our results demonstrate that the interruption probability decreases with the increase of temperature. Finally, the performance of secret key rate is analyzed with the temperature fluctuation. It is shown that secret key rate coincides positively with temperature fluctuation. Hence, the studies could contribute to evaluating the feasibility and performance of atmospheric CVQKD protocols.
Atmospheric CVQKD indicates that the parameters of protocol are closely related to atmospheric effect. The atmospheric channel plays a vital role in affecting the performance of the atmospheric CVQKD protocol. The effects of atmospheric channel on the performance of temporal pulse broadening are divided into two types: the first is atmospheric scattering and the second is atmospheric turbulence. In this paper, only the effect of atmospheric turbulence is addressed at great length.
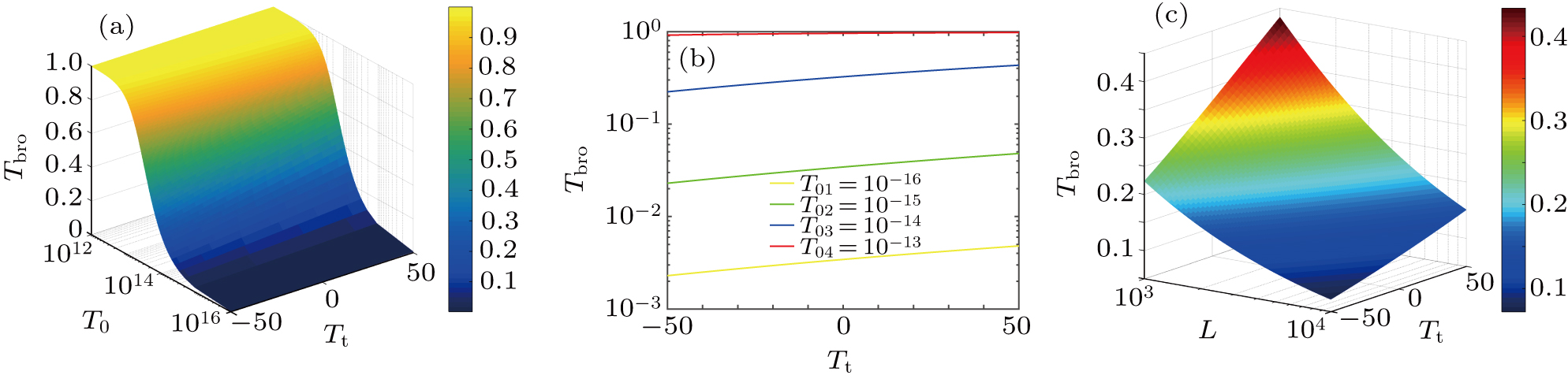
The effect of atmospheric turbulence on the atmospheric transmission of beam pulses is actually caused by the random fluctuation of atmospheric refractive index on a spatial scale. The different variance of atmospheric refractive index fluctuation represents different turbulence intensity. Because refractive index is a function of temperature in atmosphere, the properties of refractive field are closely related to the properties of temperature field. The temporal pulse broadening of atmospheric means the diffusion of pulse energy in temporal domain. In the practical experiment, signal detection is conducted in high speed sampling in temporal domain, and the maximum value is selected as the detection result, which means that the temporal pulse broadening introduces an equal transmittance. As shown in Fig.
We can evaluate the mean value of transmittance for equality via approximately calculating the intensity of free space irradiation of collimated beams under near and far field. The transmittance introduced by mean value of pulse broadening can be expressed as[27–29]
 |
 |
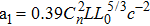
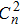
Because of the randomness, irregularity, and temporal and spatial limitation of turbulence, it is difficult to directly measure the turbulence intensity. The refractive index structure parameter describes the strength of the atmospheric refractive index, which can be used to represent the strength of turbulence. According to the structure function of Tatarskii, the refractive index structure function 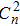
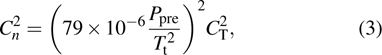 |
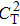
We consider pulse broadening rate, and define the pulse broadening rate as[21]
 |
Figure
The results of the relationship among initial pulse half-width, temperature and broadening rate are given in Fig.
From this analysis it can be seen that the temporal pulse broadening rate and the transmittance varying with temperature and distance can be acquired, which provides a judgment basis for the improvement of performing QKD. When implemented with other parameters, the protocol performance can be greatly improved by selecting appropriate parameters on the basis of the relationship among temperature, temporal pulse broadening and transmittance.
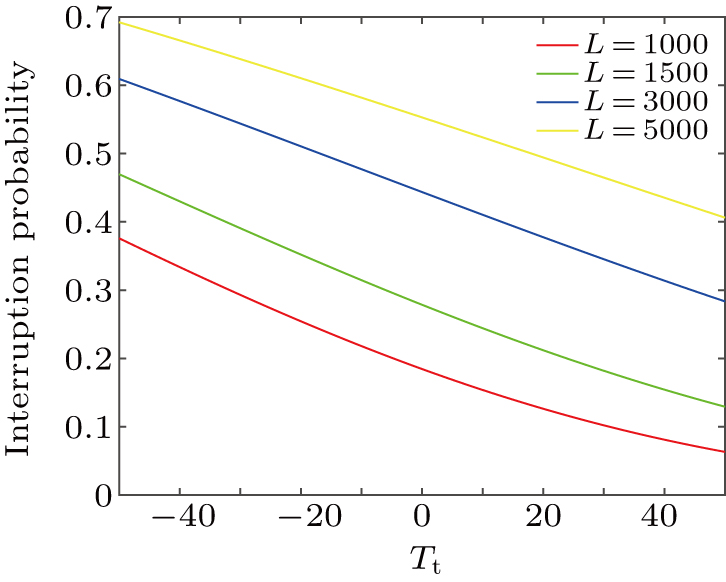
In the case of atmospheric turbulence, due to the variation of refractive index, the beam angle-of-arrival will fluctuate, which makes the communication interrupted possibly. It can be seen from the previous analysis that the refractive index corresponds to temperature fluctuation, thus the relationship between temperature and interruption probability is under consideration in this subsection.[30,31]
First, the fluctuation of angle-of- arrival is analyzed. As shown in Fig.
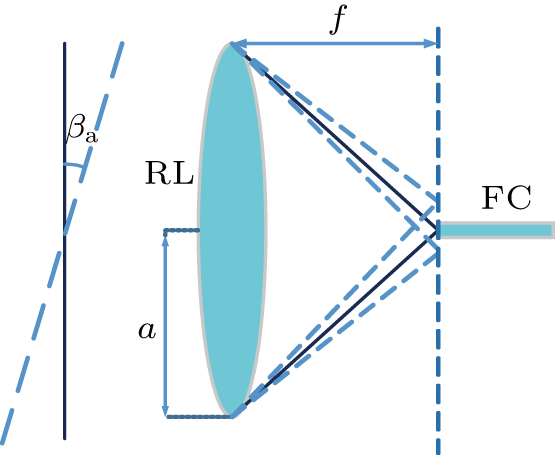 | Fig. 4. Communication interruption caused by beam fluctuations on the receiving plane. 
|
At first, we assume that the mean value of arriving angle is[21]
 |
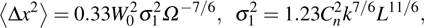 |
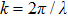

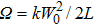
The interruption probability of communication can be shown as[21]
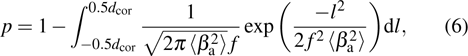 |

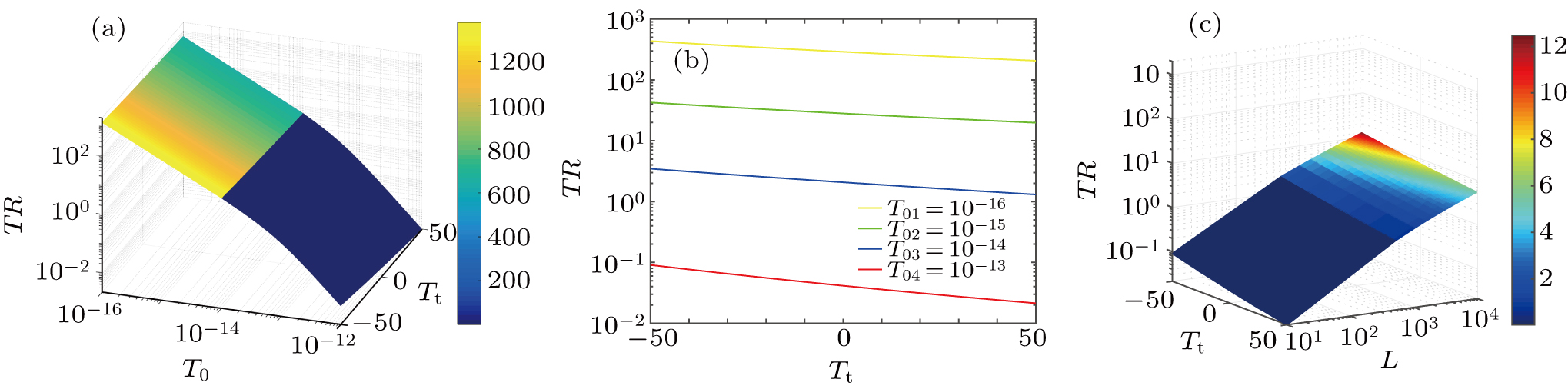
Next, the secret key rate of atmospheric CVQKD through fluctuating channel is analyzed. An atmospheric CVQKD protocol is shown in Fig.
The secret key rate K is given as[21]
 |
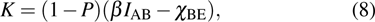 |
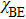
 |
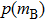
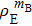
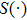
Then, we should calculate 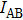
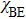
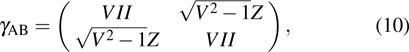 |
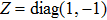
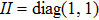
On the assumption that the state is described by distribution of probabilities of transmittance 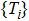
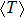
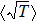
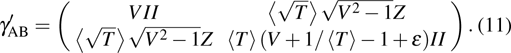 |
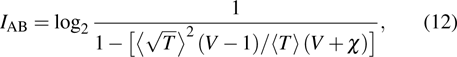 |
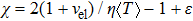
 |
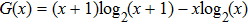
In this section, the final secret key rate in conjunction with the results from previous analyses is investigated. Here we do not consider the excess noise that changes with temperature, but we still examine the performance under different fixed excess noise levels, namely ε = 0.01, ε = 0.03, and ε = 0.05 in SNU.
First, in the analysis of the secret key rate, we consider only the effect of pulse broadening. As can be seen in Fig.
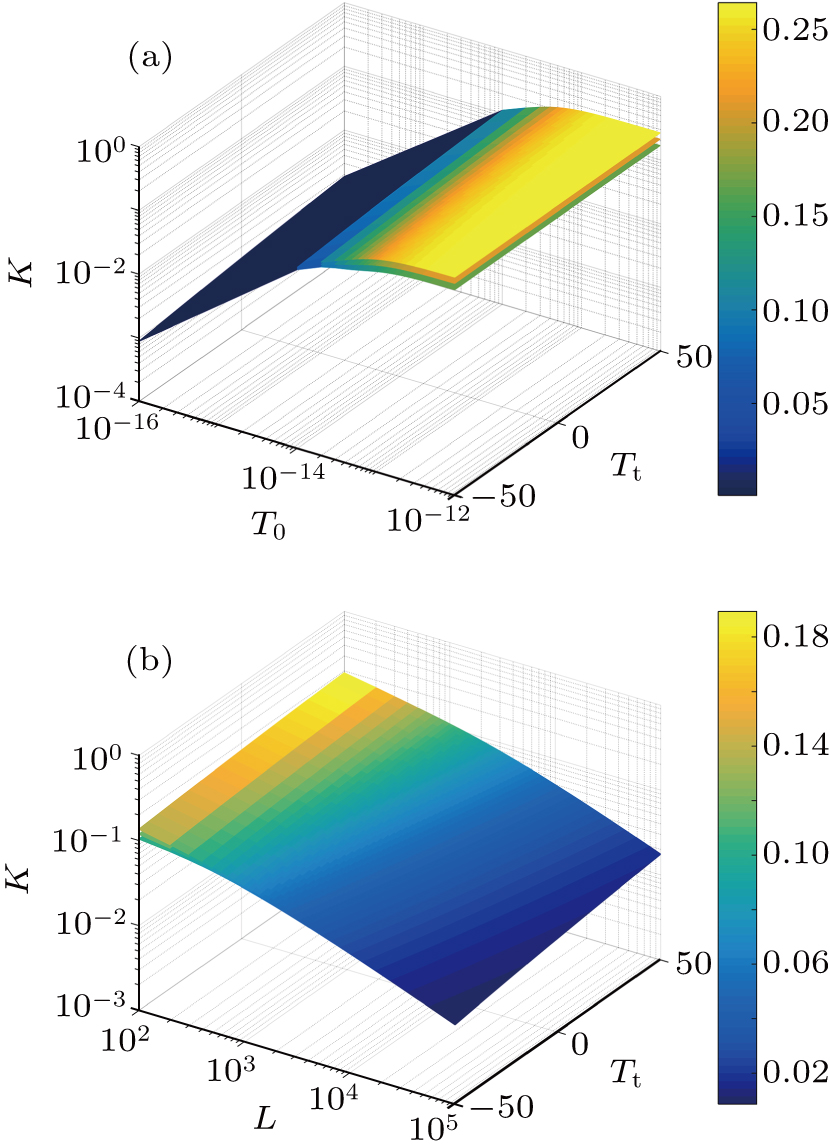 | Fig. 7. (a) Secret key rate varying with initial pulse half-width and temperature at distance 1000 m. (b) Secret key rate varying with distance and temperature at initial pulse half-width. |
Second, we take the interruption probability into consideration in the analysis of the secret key rate under diverse excess noise levels of ε = 0.01, ε = 0.03, and ε = 0.05. At the distance of 1500 m, the transmittance is 0.9. In Fig.
Finally, this analysis is comprehensively combined to analyze the final secret key rate. We estimate the secret key rate in Eq. (
In this paper, we perform an analysis of atmospheric CVQKD with the temperature effect and estimate its performance. It can be seen from the analysis that the temporal pulse broadening varies with atmospheric temperature, and the smaller the initial pulse half-width, the larger the temporal pulse broadening is, which means that in the practical application, the communication parties can choose different initial pulse half-widths according to the actual temperature to achieve the minimum temporal pulse broadening. Furthermore, we study the effect of temperature on communication interruption, and the probability of communication interruption increases with the decrease of temperature. That is to say, when we implement an atmospheric CVQKD, and consider the effect of temperature on interruption probability, we can choose a relatively high temperature to reduce the probability of interruption. We assess the secret key rate with temperature effect, initial pulse half-width and distance. According to our analysis, the increase of temperature or the decline of distance will lead the secret key rate to increase. In general, the results can conduce to the performance assessment of practical atmospheric CVQKD. However, atmospheric turbulence is exceedingly complex. Other parameters that describe atmospheric turbulence also have an influence on turbulence, which in turn affects the atmospheric CVQKD. Therefore, other factors, such as pressure, humidity and wind speed, should be taken into account in further studies.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |