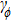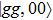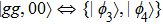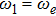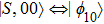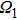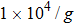† Corresponding author. E-mail:
We present a dissipative scheme to generate an entangled steady-state between two superconducting transmon qutrits separately embedded in two coupled transmission line resonators in a circuit quantum electrodynamics (QED) setup. In our scheme, the resonant qutrit-resonator interaction and photon hopping between resonators jointly induce asymmetric energy gaps in the dressed state subspaces. The coherent driving fields induce the specific dressed state transition and the dissipative processes lead to the gradual accumulation in the population of target state, combination of both drives the system into a steady-state entanglement. Numerical simulation shows that the maximally entangled state can be produced with high fidelity and strong robustness against the cavity decay and qutrit decay, and no requirements for accurate time control. The scheme is achievable with the current experimental technologies.
In the past decades, quantum entanglement[1,2] as a peculiar nonclassical effect of physical system and an indispensable resource of quantum information has been deeply studied and great progress has been made both theoretically[3] and experimentally,[4] thus greatly promotes the development of quantum computing and quantum communication. The ultimate goal of quantum information is to achieve large scale quantum computing and quantum communication. In this sense, the challenges faced by the field of quantum information in the course of development mainly come from two aspects, one is the maintenance and storage for quantum entanglement, the other is the scalability of the physical system. It is widely convinced that dissipation induced by the environment is the main obstacle in preparing and storing entanglement, for the reason that dissipation may inevitably degrade the coherence of the quantum system. From this perspective it is a negative factor for quantum information processing (QIP) and should be avoided as much as possible. However, recent theories and experiments show an interesting fact that the dissipation can be used as a positive resource for quantum computation and entanglement generation,[5–8] so that an alternative approach for engineering dissipation to generate entanglement has emerged. Many dissipation-assisted entanglement schemes have been proposed with cavity quantum electrodynamics (QED),[9–24] atomic ensembles,[25–27] ion traps,[28–30] plasmonic systems,[31–33] and optical lattices.[34,35] The relevant experimental demonstrations are also have been achieved in atomic ensembles[36] and ion traps.[30] Different from the unitary evolution schemes, these schemes use dissipation as a positive resource in the preparation process, and have the advantages in robustness against decoherence and parameter fluctuations and dose not require a specifical initial state or precise evolution time.[28]
On the other hand, circuit QED can produce an extremely strong interaction between the superconducting qubits and the microwave photons in a transmission line resonator, which is beneficial to quantum system to resist the environmental dissipation and parameter fluctuations.[37] In view of its high integratability, high tunability, and addressability for individual resonators, the circuit QED has been widely regarded as the most promising architectures for QIP.[38–41] It is essential for large scale quantum computation to engineer entanglement in coupled cavity networks, from this perspective, it would be of great importance to prepare entanglement among superconducting qubits in separated resonators. In this paper, based on the circuit QED architecture, we design an alternative scheme to prepare the entangled steady-state of two superconducting transmons separately interact with two transmission line resonators in a coupled circuit QED dimer.[42,43] The resonant transmon-resonator interaction and the photons hopping between two resonators lead to a dressed state subspace of the qutrits with different excitation numbers of photon modes. By employing two specified microwave fields to resonantly drive the system to the well-defined state in dressed state subspace and resorting to the dissipations of photon leakage and qutrit decay, a steady entanglement between two transmons can be obtained. Numerical simulations show that the entangled steady-state can be achieved with high fidelity with current experimental parameters. The scheme is independent of the initial state and robust against parameter fluctuations.
The remainder of the paper is organized as follows. In the Section
The system under consideration is depicted in Fig. 
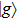





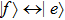

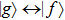


 |
 |
 |
 |
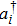
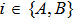
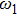
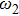
Notice that the excitation number operator of the total system 

Here, we obtain the relevant energy eigenstates of Hamiltonian HNM and use them as dressed states within the specific excitation number. The energy of level 
 |
 |
| Table 1.
The eigenstates and eigenenergies of the Hamiltonian HNM within the null-excitation subspace. Here the notation |
| Table 2.
The eigenstates and eigenenergies of the Hamiltonian HNM within the single-excitation subspace. . |
The different energy gaps between these dressed states provide the possibility to drive the specific transitions of the system with extra microwave fields.
We let the second microwave pulses applied to two transmons to be opposite in phase, i.e., 
 |
 |
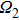


The dynamics of open dissipative system in Lindblad form is described by the master equation
 |

 |
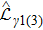
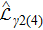
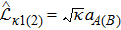

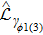
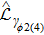
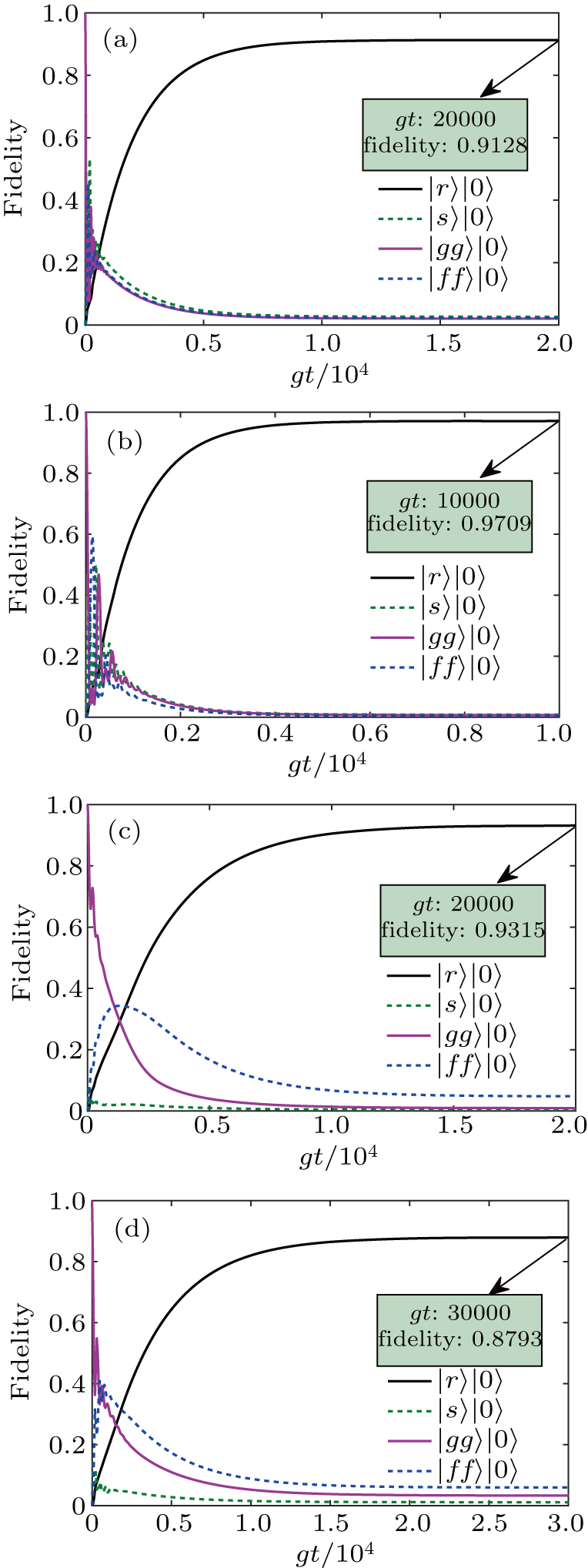
The processes for producing and stabilizing the Bell state 



























To demonstrate the feasibility of our Bell-state stabilization mechanism, we assess the performance of our scheme by numerically solving the Lindblad master equation. In Fig. 
 |
 |
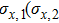
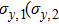
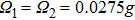
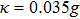
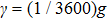
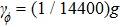
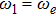
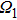
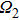
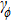
 | Fig. 4. The CHSH correlation of the target steady state as a function of the time. We choose the experimental parameters: 

|
Since charge noise may causes random fluctuations of the qutrit frequency in circuit QED, resulting in dephasing,[45] different from the qutrit decay and photon decay of the resonator, qutrit dephasing is a detrimental effect for the current scheme. In Fig. 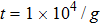




In conclusion, we have proposed a dissipative scheme for creating an entangled steady-state between two transmons separately interacts with two coupled transmission line resonators in circuit QED. The combination of coherent driving fields and dissipative processes would drive the system into a steady-state. By choosing different frequencies of the microwave field, the target steady-state can be generated with different preparation channels. The numerical simulations and analysis show that the present scheme is robust against the qutrit decay and the cavity decay due to they are used as the positive resources in the scheme. Since the transmon qubits have been demonstrated in experiments as well as its scalability in circuit QED, the current scheme can be used to physical realization of quantum computer and quantum communication.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] |