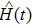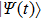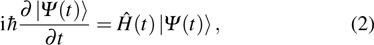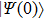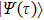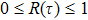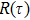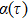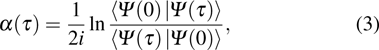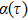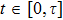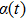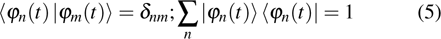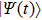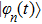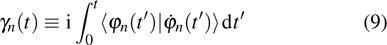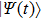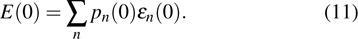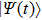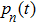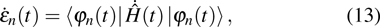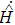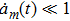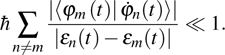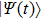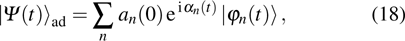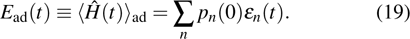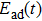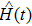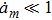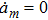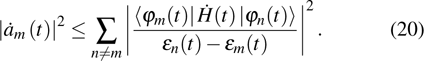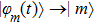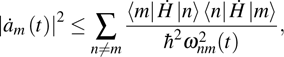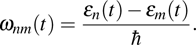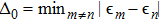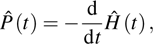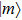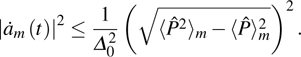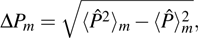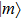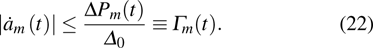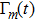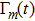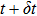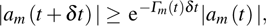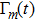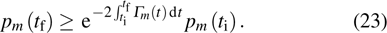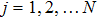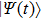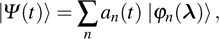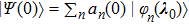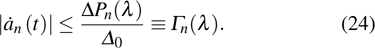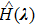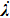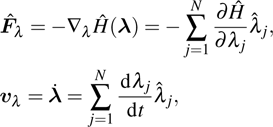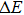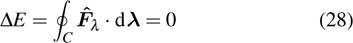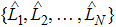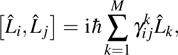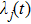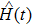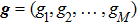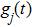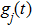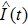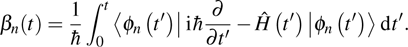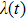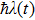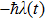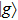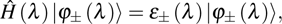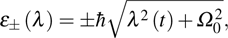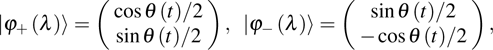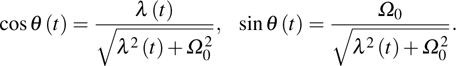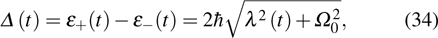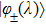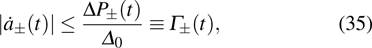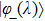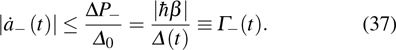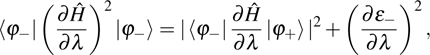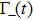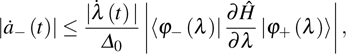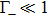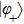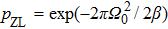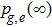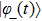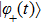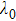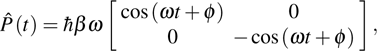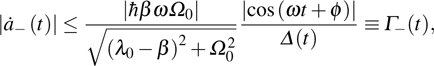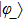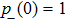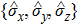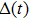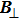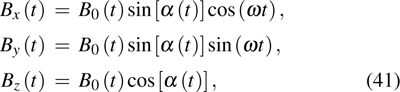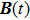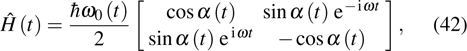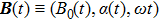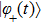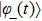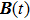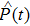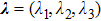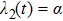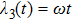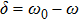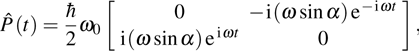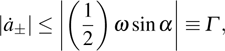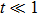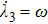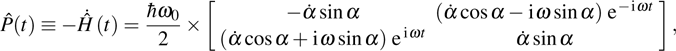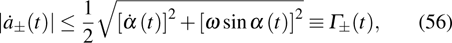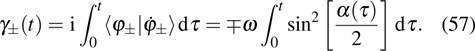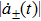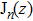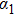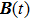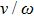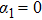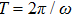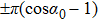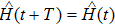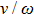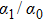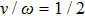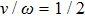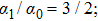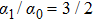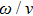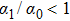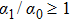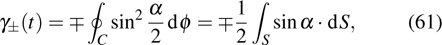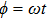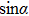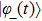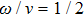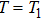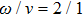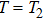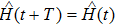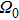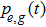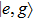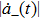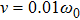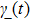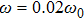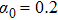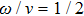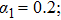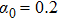Cite this Article
Zhang Lin, Liu Junpeng. The upper bound function of nonadiabatic dynamics in parametric driving quantum systems. Chinese Physics B, 2019, 28(8): 080301  
Permissions
The upper bound function of nonadiabatic dynamics in parametric driving quantum systems
Zhang Lin†, , Liu Junpeng
School of Physics and Information Technology, Shaanxi Normal University, Xi’an 710119, China

 

† Corresponding author. E-mail: zhanglincn@snnu.edu.cn

Project supported by the National Natural Science Foundation of China (Emergency Project, Grant Nos. 11447025 and 11847308).

Abstract

The adiabatic control is a powerful technique for many practical applications in quantum state engineering, light-driven chemical reactions and geometrical quantum computations. This paper reveals a speed limit of nonadiabatic transition in a general time-dependent parametric quantum system that leads to an upper bound function which lays down an optimal criteria for the adiabatic controls. The upper bound function of transition rate between instantaneous eigenstates of a time-dependent system is determined by the power fluctuations of the system relative to the minimum gap between the instantaneous levels. In a parametric Hilbert space, the driving power corresponds to the quantum work done by the parametric force multiplying the parametric velocity along the parametric driving path. The general two-state time-dependent models are investigated as examples to calculate the bound functions in some general driving schemes with one and two driving parameters. The calculations show that the upper bound function provides a tighter real-time estimation of nonadiabatic transition and is closely dependent on the driving frequencies and the energy gap of the system. The deviations of the real phase from Berry phase on different closed paths are induced by the nonadiabatic transitions and can be efficiently controlled by the upper bound functions. When the upper bound is adiabatically controlled, the Berry phases of the electronic spin exhibit nonlinear step-like behaviors and it is closely related to topological structures of the complicated parametric paths on Bloch sphere.

PACS: 03.65.Ca;03.65.Ta;03.65.Vf
Keyword:adiabatic dynamics;parametric driving;upper bound function
1. Introduction

Quantum mechanics concerns more about equilibrium properties of a system by solving stationary Schrödinger equations to find intrinsic energy structures. It is a time-independent problem and many numerical methods have been developed such as the first principle calculation based on the density functional theory. However, in recent years, more attentions turn to quantum state control in order to manipulate quantum systems in a desired manner, guiding a quantum system evolving from an initial ground state to a target state through purposely designed parametric driving.[1]

The quantum control or engineering is definitely a time-dependent problem and needs real-time feedback for a practical application, for example, in the intermediate-state guiding chemical reactions (quantum catalysis)[2] or in the adiabatic quantum computations.[3] The time-dependent problems are more complicated than stationary ones because the system is non-conservative and will evolve to nonequilibrium states far-from-equilibrium dynamic,[4] which even disables an efficient description of the system because no quantum state can survive for such a quickly driving on the system.[5] Generally, not as that in the time-independent Hilbert space, an external driving always prevents the quantum system from keeping a complete basis because the Hilbert space is generally open. Traditionally, the main analytical method to deal with time-dependent problems is the perturbation theory, which holds a complete perturbed Hilbert space because the perturbation is weak. However, in many practical situations, the weak-driving condition fails and the perturbation method is invalid even in a very short driving time. But, fortunately, in most cases, the quantum control happens between two systems with different time scales, one is a classical driving system with relatively slow characteristic frequencies, and the other is the driven quantum one holding a fast intrinsic frequency determined by its internal levels. In this situation the adiabatic theory becomes a powerful tool and the adiabatic approximation is an important condition for the adiabatic dynamics. However, the normal condition of adiabatic approximation sometimes brings controversial results which, mainly, are derived from a rough static criterion.[6] Therefore, the adiabatic theorem should be carefully used because it is significant to design a robust strategy for coherent adiabatic control. As a strict condition for adiabatic approximation requires a very slow evolution of the quantum sate, fast adiabatic evolution[7] or short-cut adiabaticity[8] in order to overcome it are also presented.

Due to the above studies on time-dependent problems, in this paper, we will consider a general state evolution in a time-dependent parametric driving system. A speed limit of the state transition and a tighter condition for adiabatic approximation are found. The existence of an upper bound function for nonadiabatic transition is related to the energy uncertainty on the speed of quantum evolution[9] and consistent with the trade-off between speed and cost in the shortcut to adiabaticity.[10] Our work reveals that the speed of non-adiabatic transition between instantaneous states is limited by the state power fluctuations relative to the minimum spectral gap of the system. Therefore, this real-time bound function can provide a necessary and sufficient condition for the adiabatic dynamics if the bound function is closely controlled by a feedback mechanism.[11] The calculations of this upper bound for adiabatic dynamics on Landau–Zener transition and electronic spin control are conducted in a general two-state time-dependent model. The adiabatic Berry phases along more complicated state loops in a high-dimensional driving parameter space are investigated.

2. Adiabatic evolution and non-adiabatic transitions
2.1. The quantum dynamics resolved by the instantaneous basis

Generally, a parametric driving quantum system can be described by the time-dependent Hamiltonian , such as the following quadratic Hamiltonian[12,13]

where all the parameters are continuous functions of time which can be used to describe the parametric driving or controlling of the quantum system. For a quantum state of the above controlled system , it evolves according to Schrödinger equation
starting from an initial state to a final state of . The overall shift of the state relative to the initial state can be described by an overlap
where and . The change of indicates a non-unitary state evolution, and the overall coherent phase accumulated during the evolution can be estimated by
which is contributed by both the state unitary evolution and the state transition process. The geometrical part of except for the dynamical part is called Pancharatnam phase (P-phase)[14] of a quantum wave.

If the Hamiltonian is Hermite, the unitary evolution keeps R(t) = 1, , no state transition occurs and the coherent phase Eq. (3) reduces to

However, the detailed evolution of R(t) and can not be resolved only by state overlap c(τ) because the state evolution in a time-dependent Hilbert space is irreversible ( ) and the coherent phase α is closely dependent on the evolutionary trajectory of the state.

As the Hilbert space of a real parametric driving system is closed (the parameters now are real functions for the Hermitian property of ), the system with time-dependent parameters admits a complete set of instantaneous eigenstates satisfying[15]

and the instantaneous states hold
for . With the above assumptions of instantaneous basis,[5] any transient state of the system can be expanded by
and then the coherent phase of state can be divided into two parts
where the first part
is called the dynamical phase because it is accumulated from its energy , and the second part
is called the geometric P-phase rediscovered by Berry.[16]

By using Eq. (6), the transient energy of any state is

with the initial energy being
Therefore, the energy change of the state induced by the parametric driving is
which depends on two aspects: (i) the change of instantaneous energies of , and (ii) the change of the population distribution of in states . The energy change of the instantaneous eigenstates is
which is determined by the average driving power of in state , while the change of population distribution is determined by
We can see that the equivalence of Eq. (14) to Eq. (2) is supported by the validity of the transient expansion of Eq. (6) based on the assumptions of Eq. (4) and Eq. (5) for the parametric driving system.

2.2. The conventional adiabatic condition and the adiabatic states

Based on instantaneous basis, we can write Eq. (14) into another form of

Clearly, equation (15) describes the nonadiabatic state transition between instantaneous eigenstates. If the parametric driving is weak, equation (15) can be directly dropped if . This gives the conventional criterion for an adiabatic approximation[17] when
which is equivalent to
The above condition actually means
which implies a very weak transition from one instantaneous state to other (transitionless quantum driving[18]). In a parameterized Hilbert space, adiabatic evolution corresponds to a parallel transportation of state vectors without any local rotations for phase accumulations. However, an overall rotation angle still be available because the parametric path is always confined to a manifold which has a geometrical curvature.

Then, if a state evolution is controlled by Eq. (16), after an evolution of time t, the state should be very near to the adiabatic state

which is obtained by , from Eq. (6). Therefore, the energy of the adiabatic state is

Comparing the adiabatic energy with Eq. (10), we can find that the energy change of an adiabatic process is only determined by the energy shifts of the instantaneous levels (an overall level shift or distortion of level profiles with respect to the systemʼs parameters). The adiabatic evolution does not change the population distribution in the eigenstates but only gives phase shifts to the initial states as Eq. (18). This implies that an adiabatic process is beyond any thermal process and keeps the population distribution unchanged. Adiabatic evolution displays a unitary evolution of a set of instantaneous eigenvectors of and only admits energy shifts following the driving parameters. That means no transition occurs during an adiabatic evolution and the level crossing (energy degenerate point) is not permitted during the adiabatic driving processes.[19]

As a reliable condition for the adiabatic approximation is a key for precise control on geometric phase, the conventional condition of Eq. (16) is weak and have been questioned by many authors such as in Ref. [20] because equation (16) only means but does not mean . Therefore, the constant condition of to drop Eq. (15) leads to many conflict results when changes with time and many improved approximate conditions were presented.[21] However, some new proposals are complicated to apply and lack of clean physical meanings. Here, we will discuss it physically to give a more general but tighter condition for the adiabatic control.

2.3. Upper bound functions for transition rates with energy gap

We can see that the conventional adiabatic condition of Eq. (16) is obtained by completely neglecting all the nonadiabatic terms in Eq. (15). Instead of dropping them, we use Cauchy–Schwarz inequality on Eq. (15) to find[22] (see Appendix B)

By using a simple notation , we can write the inequality by
where the instantaneous transition frequencies are defined by
If the eigenenergy levels of the system keep crossing avoided during the quantum evolution (without level crossings) and the minimum level gap exists , then we have and
Equation (21) indicates that the magnitude of the non-adiabatic transition rate in any eigenstates must be smaller than the variance of energy changing. Certainly, this conclusion is based on an assumption of the minimum level gap existing during the evolution. However, the adiabatic theorem beyond a gap was also discussed in Ref. [23].

If we introduce a driving power operator of the system by the negative energy changing rate of the system

then we can give an upper bound of non-adiabatic transition rate from eigenstate by
If the the power fluctuation in state is defined by
then, finally, we obtain the upper bound function for the non-adiabatic transition rate in state as
The above real-time bound function is actually a damping rate of to estimate the non-adiabatic speed in a general quantum dynamics of parametric driving. The existence of the upper bound function reveals that the transition rate from one instantaneous state to another is limited by the ratio between standard power fluctuation and the minimum level gap of the system. Or, reversely, the adiabatic approximation is valid only under the condition that the power fluctuations induced by the parametric driving is smaller than the minimum gap of the system. This real-time condition indicates that the non-adiabatic transition has a speed limit for a parametric driving system and the adiabatic process should be a slow evolution avoiding level mixing.

Based on Eq. (22), the probability amplitude in state at time can be estimated by

and the probability of remaining in state during an adiabatic driving process (for a small ) from an initial time ti to a final time tf can be roughly estimated by

3. The bound function in the driving parameter space

Considering N independent driving parameters , , of a quantum system, the Hamiltonian can be written as . At a quantum control time interval , the instantaneous eigenstates for satisfy

Then any transient state can be expanded by
starting from an initial state , and the coefficients of the transient state can be estimated by the bound function as
In the N-dimensional parameter space of , a transient state of corresponds to a point, and the power operator in the parametric Hilbert space is
where gives a gradient field of the system and describes the dynamical equations of the parameters. If we define a general parametric force of the energy field and velocity in the parameter space as
respectively, where is the unit vector, then the power of Eq. (25) will be in a familiar form
which is the same as that defined in Ref. [24]. Alternatively, the above equation gives
where is the energy change when the system evolves along a path C in the parameter space . Clearly, if the field satisfies
along any closed path, the field of the system is conservative and has no singular point in the parameter space.

Therefore, if the parameters are controlled by the external driving, the bound Eq. (24) means that the non-adiabatic transition rates of the instantaneous eigenstates are limited by the fluctuations of “work” done by force 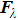per second when the state moves along the parametric driving path C. Basically, the force field of 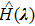is determined by the energy structure of the system and the path C depends on the solutions of the parametric equations due to the driving schemes.

Usually, a parametric driving Hamiltonian is solvable and it can be written in a form of

where the operators can generate a finite M-dimensional Lie algebra by repeated commutations,
with . In most cases, the number of independent driving parameters satisfies . Therefore, the driving parameters are piecewise continuous real functions defined on the control time interval. Surely, equation (29) is not unique and different parameterized form can be obtained by different Lie algebras defined on the diving system. Generally, the solutions of Eq. (29) can be obtained by the Lie transformation method.[13]

Further, if there exists a dynamical invariant for the above Hamiltonian in a form of[25]

then a useful parameter space of can also be introduced and the continuous complex functions at the same time interval will determined by the parametric equations of
If the parameter path can be solved from Eq. (31), then the system has an invariant variable which can be used to discuss the adiabatic control by Lewis–Riesenfeld invariants method.[25,26] It is well known that the instantaneous eigenstates of provide an optimal basis to expand by[8]
where
Compare Eq. (32) with Eq. (18), we can see a similar form of adiabatic state on this basis because the force field disappears in g-parameter space along the parametric path of Eq. (31) (the path is on a constant-energy surface). Therefore, a proper parameter space chosen to reveal the topological properties of Hamiltonian becomes important for an adiabatic control.

3.1. Bound functions for nonadiabatic transition in an avoided level crossing system with one driving parameter

Specifically, we consider a two-state system as an example, such as in a scheme of Landau–Zener transition shown in Fig. 1,[27] with only one driving parameter ,

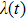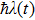
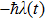
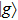
where and are the instantaneous energies of two bare states of and , and is the coupling strength between them. Then the instantaneous eigenstates of Eq. (33) satisfy
where the instantaneous energies are
and the instantaneous states are
with

Fig. 1. The avoided crossing energies of two-level system controlled by only one driving parameter . The dashed lines are the energies of bare states when the coupling rate is zero. Different sweeping processes enabled by the parametric setups are indicated by the arrows.

Here, we also introduce an instantaneous energy gap

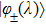
and we define . Therefore, the nonadiabatic transition rates from states have a limit of
where the power operator of the parametric Hamiltonian is defined by

3.1.1. Landau–Zener transition by linear sweeping driving

If the parameter λ(t) enables a linear sweeping scheme as

where β is the chirp-rate of the driving field. The power operator
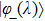
and its variance in state is

As shown in Fig. 1, the maximum nonadiabatic transition happens at the energy-level crossing point by (at λ = 0) where the energy gap in this case is

and the minimum gap is . Then the bound function in this case for state is
The above bound function reveals that the instantaneous transition rate is closely dependent on the energy gap and reaches the maximum value of at the energy-level crossing point ( ), which is often called the non-adiabatic point.

As the two-state system is closed, then

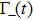
and the non-adiabatic bound can be written as
which, actually, is similar to the Fermiʼs golden rule. Therefore, the bound function gives Eq. (23) as
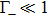
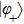
and which can be used to estimate the transition probability when . As the maximum transition rate from ground state to upper state is , the probability remaining in the state after the parametric sweeping from right to left satisfies
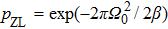
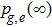
which gives a lower probability in the state after a time interval of across the energy avoided crossing point. In Fig. 2, we exactly calculate the probabilities of (thick solid lines) as well as (thin solid lines), where the bound probability of determined by Eq.(39) and the Landau–Zener formula, , for are also shown by the horizonal dashed lines. 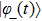If , the system will keep an adiabatic evolution with a weak transition probability from the instantaneous state to . 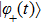As this model can be exactly solved, the upper bound function seems to be a bad estimation compared to the exact Landau–Zener formula,[28] but in a high dimensional parameter space, this bound will be a very useful tool for the real-time adiabatic control if an exact transition formula is absent.

Fig. 2. The evolutions of the probabilities (thick lines) in the instantaneous eigenstates of and (thin lines) in the bare states of . The horizonal dashed lines are the probabilities predicted by the Landau–Zener formula and the upper bound determined by Eq. (39). The parameters are , β = 0.3 Hz/s, and .
3.1.2. Landau–Zener transition by back and forth sweeping driving

If the driving parameter gives a back and forth sweeping scheme as

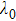
where is the level sweeping amplitude around . The power operator in this case is
and its variance is

Therefore, the real-time bound function of the transition rate is

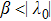
and when or , the bound function will be

Figure 3 demonstrates the transition bound and reveals that the transition rate is closely dependent on the energy gap of the system and, for all the above cases, the bound function reveals a closer condition than the conventional adiabatic approximation of

Fig. 3. The evolutions of the instantaneous energies of eigenstates and the bound function of . The parameters are λ0 = 12 Hz, β = 1.4 Hz, and Ω0 = 0.4 Hz.

As there is no explicit analytical formula for transition probability in this case, the bound functions can give a rough transient estimation of the probability remaining in the state

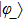
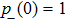
when the system starts from the ground state for . Surely, this probability is a very bad prediction for a longtime evolution, but the bound function Γ(t) can provide a better real-time estimation of the non-adiabatic transition rate for a robust feed-back adiabatic control during transitionless quantum driving for time-dependent quantum systems.

3.2. Adiabatic control of spin by the sweeping magnetic fields

Now, let us calculate the upper bound function with more driving parameters in the two-state system with a general form of

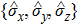
The Hamiltonian can be expressed by Pauli operators in a form of Eq. (29)
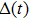
where and the parameters and can be any time-dependent functions for different driving schemes in a practical control process.

A typical application of the above model is for spin qubit control with a varying magnetic field shown in Fig. 4. The driving magnetic field is usually constructed by superposition of two varying magnetic fields, one is along z direction and the other 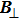is perpendicular to and rotates with a frequency of ω.[16] The combined magnetic field can be generally described by

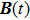
where the magnitude of is B0(t) and α (t) is the instaneous angle of the sweeping cone. The spin Hamiltonian reads
where the Lamor frequency of electron spin is

Fig. 4. The control of electronic instantaneous spin states by (a) a magnetic field in z direction and (b) a sweeping magnetic field denoted by spherical coordinates of .

As the sweeping magnetic field can be denoted by a spherical coordinate: 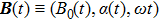, we can introduce three spherical driving parameters as

then the Hamiltonian of Eq. (42) is put into a form of
which is defined in λ-parameter space. Alternatively, another popular parameterized form,
is often used to define a generalized Bloch sphere where the new parameters are defined by
and we can easily find that the Bloch parameters u(t), v(t), and w(t) satisfy

It is well known that the spin operators construct a SU(2) Lie algebra and the instantaneous spin eigenstates and eigenvalues are

which gives an energy gap of .

The instantaneous eigenstates 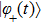and 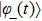represent the spin-up and spin-down states with respect to the transient direction of the magnetic field , respectively. As spin states follow the direction of 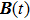controlled by the driving parameters , , and , the physical conditions for a practical spin control satisfy (or ) because the internal Lamor frequency of electronic spin ( ) is much larger than the varying speed of the classical driving parameters.

The general spin state Ψ(t) can then be expanded by

where the dynamical phases are

In this case, the dynamical equations for the transition rates are

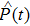
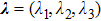
and the transient power operator of Hamiltonian Eq. (42) with parameters reads

We can easily verify that equation (50) satisfies Eq. (26) and the parametric path is determined by the driving scheme of Eq. (44). Therefore, the upper bound for non-adiabatic transition rate in this case can be estimated by Eq. (24) in details if the time-dependent functions of the driving parameters are given. In the following sections, the bound functions of adiabatic control with two different driving schemes are calculated and the geometric phases for the adiabatic spin dynamics are investigated.

3.2.1. Magnetic field sweeping in the azimuthal direction

A magnetic field sweeping in the azimuthal direction with a fixed polar angle α is a conventional scheme to drive electronic spins, which is realized by the driving parameters of , , 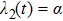and 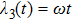(see Fig. 4), and the transition dynamics for this control scheme will be

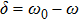
where the detuning . Consequently, the power operator reduces to
and the upper bound for non-adiabatic transition rates calculated by Eq. (24) are
which can also be directly obtained from Eqs. (51) and (52), leading to a convectional adiabatic condition of adiabatic control for . When the spin is initially in spin-down state, the probability estimation of Eq. (23) on spin-up state at a later time will be checked by the strict solution of
where the effective flip frequency is
and equation (23) gives
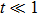
which is exactly the expansion of Eq. (53) at a very short time . As the rigorous solution of this case is well studied,[15] the geometric phase in this case is omitted.

3.2.2. Magnetic field sweeping in both azimuthal and polar directions

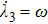Now we would like to consider a more general controlling magnetic field for , , and , then the driving power operator of the system is

and the transition dynamics for this control scheme are
The upper bound function of this control scheme becomes
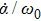
which sets the modulus bound for the changing rates of both driving parameters as shown in Fig. 5. When both the changing rates and keep small, the dynamics will conduct an adiabatic evolution which leads to an adiabatic geometric phases for as

Fig. 5. The evolutions of the transition rate (red thin lines), (blue thin lines) and their upper bound functions (black lines). The control parameters are , , , (a) and (b) , with the initial probabilities .

Specifically, if the polar angle of 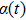is controlled by a periodic function of

the upper bound function for the adiabatic control reads

The dynamics of transition rates 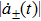and the bound function are both shown in Fig. 5 for different driving parameters. The bound function exhibits a good real-time constraint on the transition rate and reveals that low sweeping frequencies (ω and ν) and small sweeping amplitude α1 are critical for an adiabatic state evolution.

For an adiabatic case of , the adiabatic geometric phase along a parametric path will be strictly calculated by

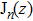
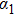
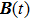
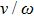
where is the Bessel function of the first kind, is the initial polar angle, and ν are the sway amplitude and frequency of the driving magnetic filed along the polar direction. Figure 6 compares the dynamics of strict phases with the geometric phases of for the instantaneous spin-down state under different frequency ratios and . The strict calculations on Eqs. (54) and (55) (the thin blue lines) verify that equation (58) is a very good result when the bound function keeps small. However, if the parametric driving breaks the requirement of a small bound function, equation (58) becomes inaccurate and the real phase of will deviate from Eq. (58) with irregular oscillations due to the non-adiabatic state transitions.

Fig. 6. The geometric phases for instantaneous eigenstate under different driving parameters. The thick black solid lines are the analytical solutions of Eq. (58), the thin blue lines are the real phases calculated by Eqs. (54) and (55), the black dotted diagonal lines are the first term of Eq. (58) and the horizonal lines are labeled by Eq. (59) in different driving periods. Insets: the parametric paths of three different driving schemes in the Bloch space, and all the driving paths are counterclockwise. The driving parameters are , (a) , (b) , , and (c) , , .

The dynamics of the nonlinear geometric phase in an adiabatic process can be divided into two different parts: the linear part which increases linearly with time (the dotted lines in Figs. 6(b) and 6(c)) and the nonlinear part which induced by the parametric oscillation in the polar direction. The adiabatic geometric phases related to two periods of and are

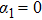
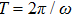
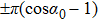
which are displayed in Fig. 6 by the grey horizontal grid lines just for references. Clearly, in a conventional case of , equation (58) gives the familiar Berry phase in a cyclic period of with a solid angle of , deriving only from the linear part of Eq. (58) (see Fig. 6(a)). However, for a control period of T = 2π/ν along a closed parametric path for , the invariant Berry phase will be

As we have two control frequencies, ω and ν, along the azimuthal and polar directions, respectively, there exist two evolutionary periods of T for 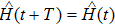that will lead to rich geometric structures of the Lissajous parametric paths on Bloch sphere determined by the frequency ratio of 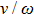and the amplitude ratio of 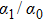(see Fig. 7). Therefore, the Berry phase in this case should be determined by a common period covering a closed path in the parameter space.

Fig. 7. The parametric paths of different driving schemes in the parameter space of Bloch sphere. The driving parameters are , , (I) , (II) , (III) , and (IV) , .

For the adiabatic dynamics, when the driving ratio 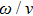is a rational number, that is , where , the common period is while the adiabatic geometric phase is . For 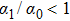, the path has a simple form and does not intersect with itself. But for 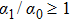, the orbit intersects with itself and the region S covered by the path on the Bloch sphere will be divided into different overlapped areas and each area enclosed by a loop contributes its respective part because the total covering area is the sum of them. This is due to

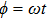
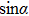
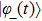
where is the azimuthal angle of the path C on the Bloch sphere and is the area element of the region S covered by the path. Equation (61) reveals a -weighted area contribution to the geometric phase. That means when the polar angle α is constant ( ), the state evolves along a circle path on the Bloch sphere and its geometric phase increases linearly with a slope proportional to as shown in Fig. 6(a). 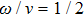Figure 6(b) demonstrates that, for a case of and , the path has a knot shape and the region S is divided into two separated areas by one intersection point (one vertex). Therefore the phases exhibit a two step-like dynamics during the command period of . 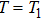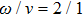While, for and , Figure 6(c) shows that the region S consists of two overlapped areas, which leads to a different phase dynamics with only one step during the command period of . 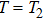The areas enclosed by more loops formed by the complicated periodic paths are shown in Fig. 7 and the parametric path has a close relation to a Eulerian path in a view of graph theory. 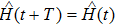However, when the ratio is an irrational number, no closed path can be found in the parameter space to fulfill and no invariant Berry phase exists in this case because the parametric path does not enclose an area (no enclosed boundary).

Therefore, the above analysis indicates that the phase evolution of a quantum state is closely associated with the geometric structure of its evolutionary path in the parameter space. Above all, the topological property of the Berry phase can be perfectly controlled by the parametric paths through a designed parametric driving under the control of the time-dependent bound function proposed in this paper.

Reference
[1] Dong D Petersen I R 2010 IET Control Theory and Appl. 4 2651
[2] Ospelkaus S Ni K K Wang D de Miranda M H G Neyenhuis B Quéméner G Julienne P S Bohn J L Jin D S Ye J 2010 Science 327 853
[3] Albash T Lidar D A 2018 Rev. Mod. Phys. 90 015002
[4] Eisert J Friesdorf M Gogolin C 2015 Nat. Phys. 11 124
[5] Deffner S Lutz E 2013 Phys. Rev. Lett. 111 010402
[6] Marzlin K P Sanders B C 2004 Phys. Rev. Lett. 93 160408
[7] Petiziol F Dive B Mintert F Wimberger S 2018 Phys. Rev. A 98 043436
[8] Torrontegui E Ibá nez S Martínez-Garaot S Modugno M del Campo A Guéry-Odelin D Ruschhaupt A Chen X Muga J G 2013 Adv. At. Mol. Opt. Phys. 62 117
[9] Pfeifer P 1993 Phys. Rev. Lett. 70 3365
[10] Campbell S Deffner S 2017 Phys. Rev. Lett. 118 100601
[11] Tong D M 2010 Phys. Rev. Lett. 104 120401
[12] Choi J R Nahm I H 2007 Int. J. Theor. Phys. 46 1
[13] Zhang L Zhang W P 2016 Ann. Phys. 373 424
[14] Pancharatnam S 1956 Proc. Indian Acad Sci. A 44 247
[15] Griffiths D J 2005 Introduction to Quantum Mechanics 2 Upper Saddle River Pearson Prentice Hall
[16] Berry M V 1984 Proc. R. Soc. Lond. A 392 45
[17] Aguiar Pinto A Nemes M Peixoto de Faria J Thomaz M T 2000 Am. J. Phys. 68 955
[18] Berry M V 2009 J. Phys. A Math. Theor. 42 365303
[19] Sarandy M S Lidar D A 2005 Phys. Rev. A 71 012331
[20] Du J F Hu L Z Wang Y Wu J D Zhao M S Suter D 2008 Phys. Rev. Lett. 101 060403
[21] Comparat D 2009 Phys. Rev. A 80 012106
[22] Cao H X Guo Z H Chen Z L Wang W H 2013 Sci. China-Phys. Mech. Astron. 56 1401
[23] Avron J E Elgart A 1999 Commun. Math. Phys. 203 445
[24] Venkatesh B P Watanabe G Talkner P 2015 New J. Phys. 17 075018
[25] Lewis H R Jr. Riesenfeld W B 1969 J. Math. Phys. 10 1458
[26] Chen X Ruschhaupt A Schmidt S del Campo A Guéry-Odelin D Muga J G 2010 Phys. Rev. Lett. 104 063002
[27] Shevchenko S N Ashhab S Nori F 2010 Phys. Rep. 492 1
[28] Wittig C 2005 J. Phys. Chem. B 109 8428