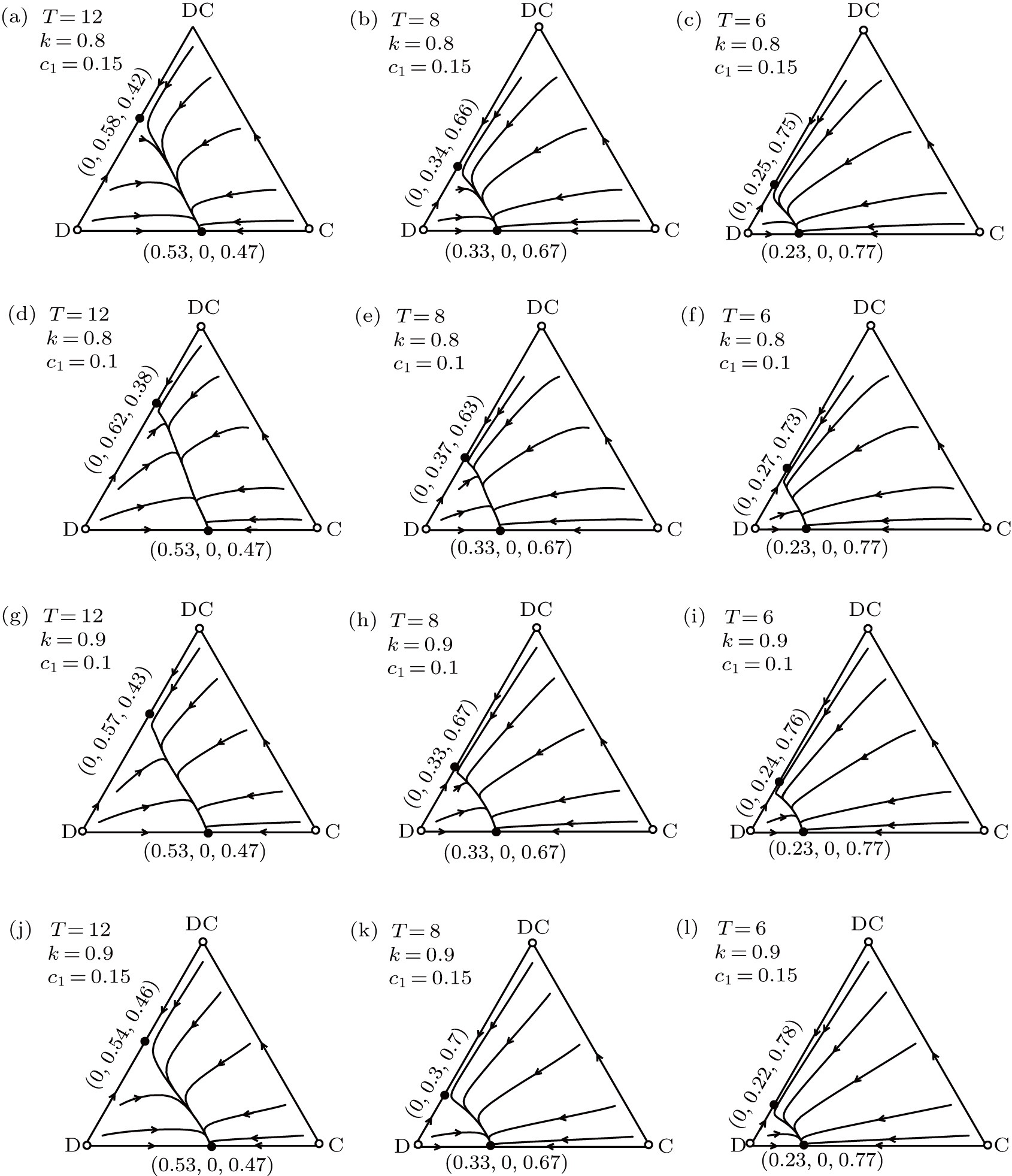
The evolution of cooperation in public good game with deposit
Evolutionary dynamics of C, DC, and D strategies for different values of T. Nodes C, DC, and D of the simplex denote homogeneous population of C-players, DC-players, and D-players respectively. And open cycles represent unstable equilibrium points and filled cycles means stable points in these pictures. For given T values and c1 values, the fraction of DC-players in the stable state on the D–DC edge decreases as k increases. For given T values and k values, the fraction of DC-players and C-players increase as T increases respectively. Besides, for given values of k and c1, the larger the value of T, the larger the fraction of C-players on the edge of C–D edge and DC-players in the edge of DC–D edge respectively. For given T values, the fraction of C-players in the stable state on the D–C edge remain unchanged irrespective of the values of k and c1. Other parameters values are N = 20,