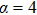† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 71771204 and 91546201).
There are various types of pyramid schemes that have inflicted or are inflicting losses on many people in the world. We propose a pyramid scheme model which has the principal characters of many pyramid schemes that have appeared in recent years: promising high returns, rewarding the participants for recruiting the next generation of participants, and the organizer takes all of the money away when they find that the money from the new participants is not enough to pay the previous participants interest and rewards. We assume that the pyramid scheme is carried out in the tree network, Erdös–Réney (ER) random network, Strogatz–Watts (SW) small-world network, or Barabasi–Albert (BA) scale-free network. We then give the analytical results of the generations that the pyramid scheme can last in these cases. We also use our model to analyze a pyramid scheme in the real world and we find that the connections between participants in the pyramid scheme may constitute a SW small-world network.
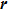
Besides RenRenGongYi, there are many more platforms of this form and Chinese government has warned about the risk of consumption rebate platforms.[2] There are many other forms of pyramid schemes, such as IGOFX[3] that originated in Malaysia and MMM[4] that originated in Russia.
Pyramid schemes are different from ordinary Ponzi schemes, which are named after the eponymous fraudster Charles Ponzi, though in both Ponzi and pyramid schemes, existing investors are paid by the money from new investors.[5] In a Ponzi scheme, the participants believe they are actually earning returns from their investment. While in a pyramid scheme, the participants are aware that they are earning money by finding new participants—they become part of the scheme.
Pyramid schemes and Ponzi schemes have been researched from many different perspectives. Joseph Gastwirth proposed a probability model of a pyramid scheme and concluded that the vast majority of participants have less than a 10% chance of recouping their initial investment.[6] Stimulated by the Madoff investment scandal in 2008, Marc Artzrouni put forward a first order linear differential equation to describe Ponzi schemes.[7] The model that was developed by Marc Artzrouni depends on the following parameters: a promised but unrealistic interest rate, the actual realized nominal interest rate, the rate at which new deposits are accumulated, and the withdrawal rate. Marc Artzrouni gave the conditions on these parameters for the Ponzi scheme to be solvent or to collapse. The model was fitted to data available on Charles Ponzi’s 1920 eponymous scheme and illustrated with a philanthropic version of the scheme. Tyler Moore et al. conducted an empirical analysis of these high yield investment programs but did not put forward a mathematical model.[8] A high yield investment program (HYIP) is considered to be an online Ponzi scheme because it pays outrageous levels of interest using money from new investors. In contrast from the traditional Ponzi schemes, there are many sophisticated investors who understand the fraud but who hope to profit by joining early, while the investors cannot withdraw their money at any time. Peihua Fu et al. researched some problems when the Ponzi scheme diffuses in complex networks.[9,10]
Since the introduction of random networks, small-world networks, and scale-free networks, complex networks have attracted great attention from researchers in various fields, such as management and statistical physics. Researches show that many natural and social phenomena have small-world or scale-free characteristics. At present, complex networks have been successfully applied to improve transportation networks,[11,28] analyze innovative networks,[28] research the spread of infectious diseases and rumors.[28,28]
Most of the existing literature focuses on the research of Ponzi schemes, including the spread of Ponzi schemes in complex networks, while the research on pyramid schemes is relatively scarce. To the best of our knowledge, for the pyramid schemes of consumption rebate type, no scholar has put forward a model at present. To understand and explain the operation mechanism and characteristics of the pyramid schemes of consumption rebate type, then provide ideas for monitoring this kind of pyramid schemes, and offer the basis for further research, we propose a pyramid scheme model which has the principal characters of many pyramid schemes appeared in recent years: promising high returns, rewarding the participants, recruiting the next generation of participants, and the organizer will take all the money away when he finds the money from the new participants is not enough to pay the previous participants interest and rewards. We assume that the pyramid scheme carries on in the tree network, Erdös–Réney (ER) random network, Strogatz–Watts (SW) small-world network, or Barabasi–Albert (BA) scale-free network, respectively, then give the analytical results of how many generations the pyramid scheme can last in these cases. We also use our model to analyze a pyramid scheme in the real world and we find the connections between participants in the pyramid scheme may constitute a SW small-world network.
This paper is organized as follows. In Section 2, we briefly introduce the tree network, the random network, the small-world network, and the scale-free network. In Section 3, we propose our pyramid scheme model. In Section 4, we analyze a pyramid scheme in real world. Some discussions and conclusions are given in Section 5.
Tree networks are connected acyclic graphs. The word tree suggests branching out from a root and never completing a cycle. Tree networks are hierarchical, and each node can have an arbitrary number of child nodes. Trees as graphs have many applications, especially in data storage, searching, and communication.[28]
Random network, also known as stochastic network or stochastic graph, refers to a complex network created by stochastic process. The most typical random network is the ER model proposed by Paul Erdös and Alfred Réney.[28] The ER model is based on a natural construction method: suppose there are n nodes, and assume that the possibility of connection between each pair of nodes is constant 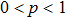
The original model of small-world was first proposed by Watts and Strogatz, and it is the most classical model of small-world network, which is called SW small-world network.[28] The SW small-world network model can be constructed as follows: take a one-dimensional lattice of L vertices with connections or bonds between nearest neighbors and periodic boundary conditions (the lattice is a ring), then go through each of the bonds in turn and independently with some probability ϕ “rewiring” it. Rewiring in this context means shifting one end of the bond to a new vertex chosen uniformly at random from the whole lattice, with the exception that no two vertices can have more than one bond running between them and no vertex can be connected by a bond to itself. The most striking feature of small-world networks is that most nodes are not neighbors of one another, but the neighbors of any given node are likely to be neighbors of each other and most nodes can be reached from every other node by a small number of hops or steps. It has been found that many networks in real life have the small-world property, such as social networks,[28] the connections of neural networks,[28] and the bond structure of long macromolecules in the chemical.[28]
A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. The first model of scale-free network was proposed by Barabasi and Albert, which is called BA scale-free network.[28] The BA model describes a growing open system starting from a group of core nodes, new nodes are constantly added to the system. The two basic assumptions of the BA scale-free network model are as follows: (i) from m0 nodes, a new node is added at each time step, and m nodes from the m0 nodes are selected to be connected to the new node (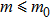
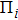
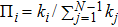
We consider a simple pyramid scheme that meets the basic features of many pyramid schemes in the real world, especially the consumption rebate platforms. First, it has an organizer that attracts participants through promising a high rate of return compared to the normal interest rate. Besides the promising return, any participant will be rewarded by the organizer with a proportion of the total investment of the participants he or she directly attracted, thus the early participants will be motivated enough to recruit the next-generation participants and the next-generation participants will do the same thing in order to get more returns. Secondly, we assume all the participants at current generation are recruited by the participants at the upper generation, and the organizer pays the participants at the previous generations the interests and rewards when all possible participants at current generation have joined in the scheme. The third assumption is that the organizer will take all the money away when he finds the money from the new participants is not enough to pay the previous participants interest and rewards. To simplify the model, we also assume all the participants invest the same amount of money and invest only once. Figure
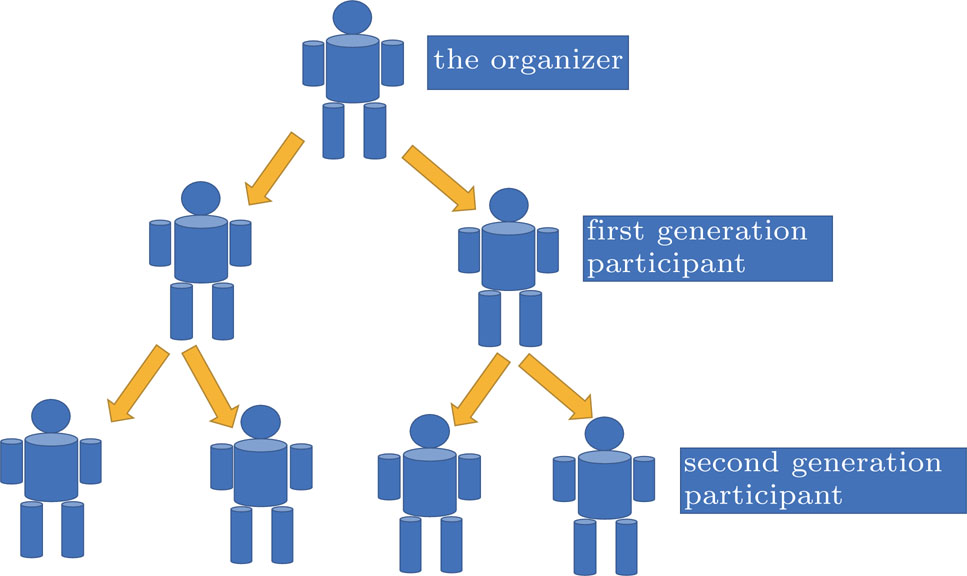 | Fig. 1. A schematic diagram of pyramid scheme. From top to bottom are the organizer, the first generation participants, and the second generation participants. |
Based on these assumptions, we discuss the pyramid scheme spreads in the tree network, random network, small world network, and scale-free network below.
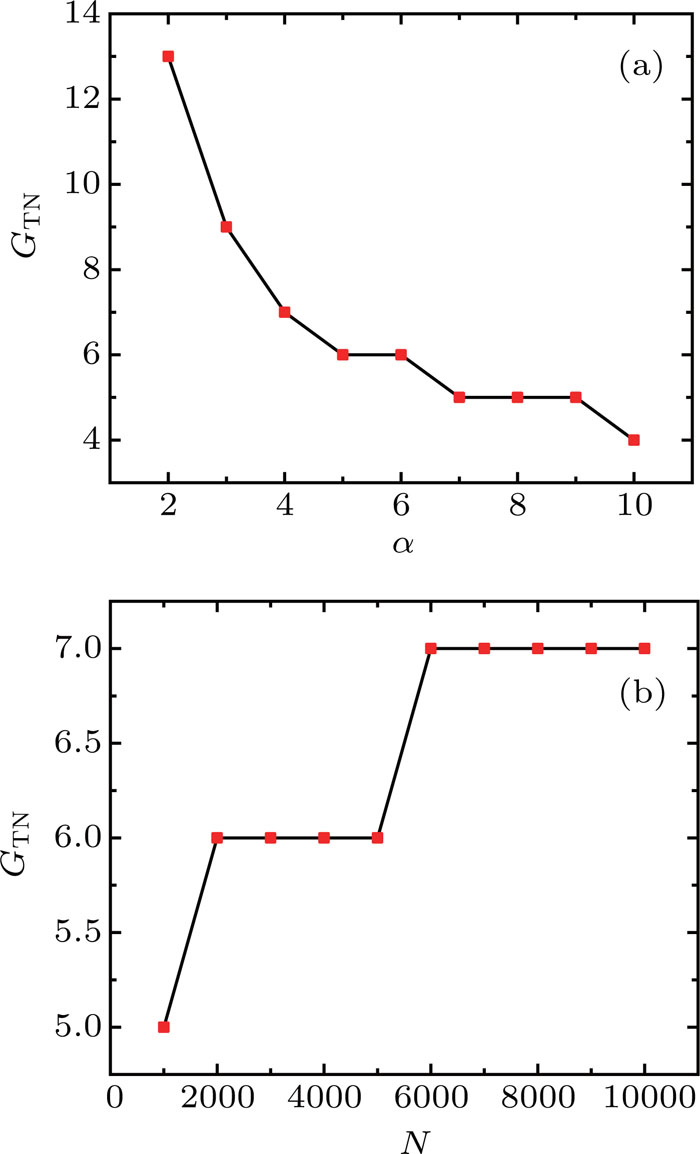
If the pyramid scheme expands in the form of tree network that has a constant branching coefficient α and the root node of the tree network represents the organiser, we can simply write the number of participants at the g-th generation as 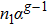
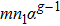
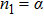
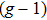
The second term of Eq. (

However, the potential participants are limited to N and the pyramid scheme will stop eventually. The maximum generation G of the pyramid scheme is given by
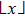
Figure 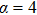
If the pyramid scheme takes place in an ER random network that has an average degree k and N nodes, we assume the organizer is a random node in the network and other nodes represent the potential participants. The organizer recruits the potential participants nearest to him as the first generation participants, and the first generation participants recruit the potential participants nearest to them as the second generation participants, and so on. So the generation of any participant in the pyramid scheme is given by the shortest path length to the node representing the organizer. Reference [28] has given the approximate analytical results for the distribution of shortest path lengths in ER random networks, the number of nodes at the i-th generation is about 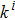
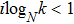

First, like the case in the tree network, r0, r1, and k should satisfy the following condition:
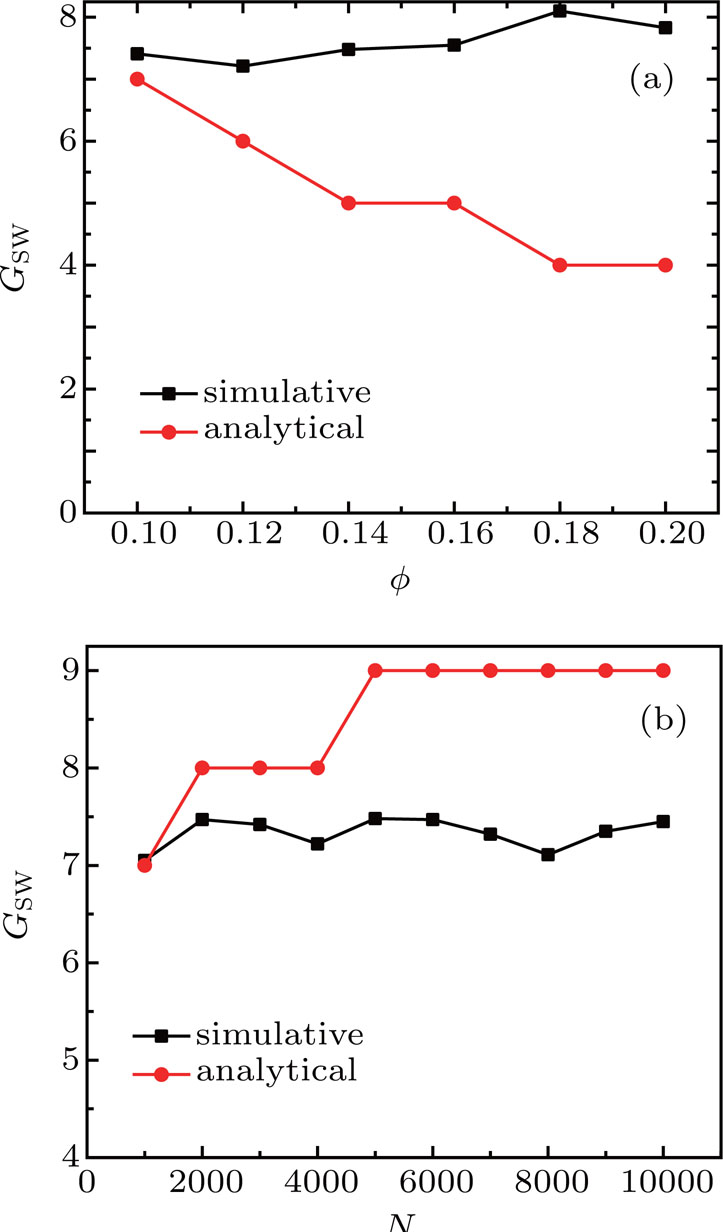
Now we consider the pyramid scheme carries out in an SW small-world network, to some extent this case is similar to the case in the ER random network. We also randomly choose a node as the organizer, other nodes represent the potential participants, and r0, r1 represent the interest rate and reward ratio, respectively. The generation of any participant in the pyramid scheme is the shortest path length to the node representing the organizer. Reference [28] pointed out that the number of nodes increases exponentially with the average length of the shortest path when the nodes are infinite. The approximate surface area of a sphere of radius r on the SW small-world network can be given by[28]

Changing r to g, we can obtain the approximate number of participants at the g-th generation. Because of the exponential form of A(g), we can deal with this case just like in the cases of tree network and ER random network. The branching coefficient α should be replaced by 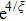
If the nodes are finite, then the number of nodes reaches the maximum when the distance from the node to the organizer is near the average length of the shortest path. If the distance is greater than the average length of the shortest path, the number of nodes quickly reduces to 0, so it can be approximately considered that the maximum generation G is close to the average length of the shortest path. The average path length 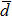
In the simulation, we find that the values of r0 and r1 are very important. Generally speaking, the greater the values of r0 and r1 satisfying Eq. (
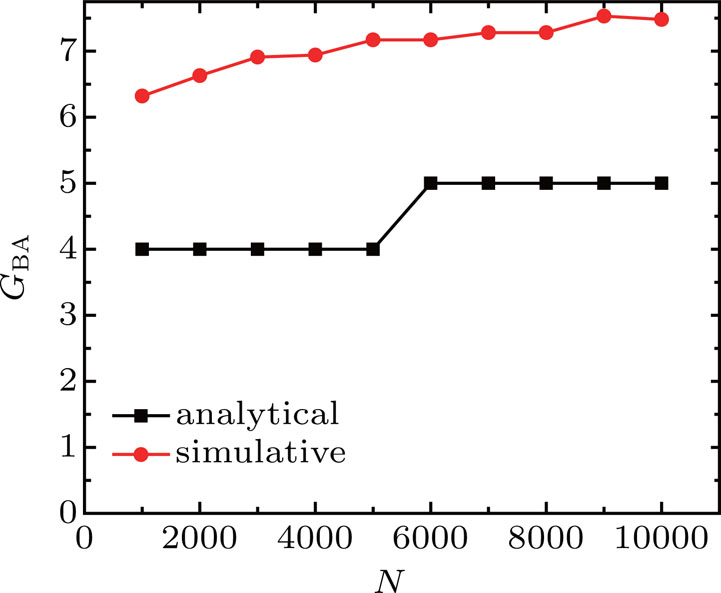
If the pyramid scheme expands in a BA scale-free network, similar to the cases in ER random network and SW small-world network above, then we also randomly choose a node as the organizer and and other nodes represent the potential participants. The organizer recruits participants and the participants recruit the next generation participants through the network connections. To ensure positive inflows, the following condition must be satisfied:
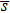
Before the peak, the number of participants per generation grows faster than the exponential growth. But after that, the number of participants per generation declines rapidly, so the condition can no longer be satisfied. So we can infer that the maximum generation GBA is close to the average shortest path length, and is given by
Figure
Although real cases of pyramid scheme are easy to find in news reports, there are few cases that give details of the number of people involved and the pyramid generations. Usually, when the organizer of the pyramid scheme disappears, the participants with loss will report the case to the police, who will then investigate the case. On July 23, 2018, China news network Guangzhou Station reported a pyramid scheme that had 75663 account numbers and 46 generations, and the pyramid scheme had amassed 76 million yuan in three months.[28] This is the same type of pyramid scheme as described in the introduction. Using the analysis in section
If this real pyramid scheme expands in a tree network, we can calculate the tree network’ branching coefficient 
If this real pyramid scheme spreads in an ER Random network, we can calculate the average degree 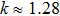


If this real pyramid scheme carries out in a BA scale-free network, through the analysis and simulation, we find that developing to 46 generations needs far more than 75663 participants. Therefore, the connections between participants are impossible to form a BA scale-free network.
If this real pyramid scheme takes place in a SW small-world network and accords to all our assumptions, then we could find a simulative result to fit the result of the real pyramid scheme. The parameters we select are N = 100000, ϕ=0.02, K = 4, r0=0.1, r1=0.1, and each participant invests 23500 yuan. The simulative pyramid scheme has 74652 participants, and develops to 46 generations, and the fund pool of the pyramid is about 76 million yuan. The simulation results are in good agreement with the real pyramid scheme. Figure
Figure
Through this simulation analysis, we can speculate that the connections between participants in the real case may constitute a SW small-world network.
In summary, we have proposed a pyramid scheme model that has the principal characteristics of many of the pyramid schemes that have appeared in recent years: promising high returns and rewarding the participants attracting the next generation of participants. Assuming that the pyramid scheme spreads in the tree network, ER random network, SW small-world network and BA scale-free network, we give the conditions for the continuity of the pyramid scheme, and the analytical results of how many generations the pyramid scheme can last if the organizer of the pyramid scheme takes all the money away when he/she finds the new money is not enough to pay interest and incentives. We also use our model to analyst a pyramid scheme in the real world and the result displays that the connections of participants in the pyramid may have the feature of small world.
Our work is helpful to understand the operation mechanism and characteristics of the pyramid schemes of consumption rebate type. Our model may be able to apply to some current illegal high-interest loans, if these illegal projects promise a high interest rate and reward the investors who encourage others to invest in such projects but the money accumulated is not actually invested in any real projects. Our work shows that the pyramid schemes of consumption rebate type are not easy to be detected by the supervision because of the small amount of funds and the small number of participants accumulated in the initial stage. After the rapid growth of funds and participants, it often comes to the end of this kind of pyramid frauds, and the organizers have often already fled. So for regulators, it is better to nip such platforms in the bud to avoid any more people suffering a loss. In addition, to some extent, our work provides some basis for further study of such frauds. For example, we will further consider how the participants’ beliefs about always having enough new participants affect the operation of these frauds.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] |