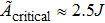† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61604106) and Shandong Provincial Natural Science Foundation, China (Grant No. ZR2014FL025).
The topological magnon insulator on a honeycomb lattice with Dzyaloshinskii–Moriya interaction (DMI) is studied under the application of a circularly polarized light. At the high-frequency regime, the effective tight-binding model is obtained based on Brillouin–Wigner theory. Then, we study the corresponding Berry curvature and Chern number. In the Dirac model, the interplay between a light-induced handedness-dependent effective DMI and intrinsic DMI is discussed.
A topological insulator is a material that has a bulk band gap like an ordinary insulator but whose surface contains conducting states.[1,2] The search for topological states of quantum matter is one of the hottest topics in condensed matter physics. The topologically protected edge states is not unique to electronic systems. A growing number of studies investigate the possibility of topological properties on magnons in two-dimensional (2D) honeycomb systems[3–12] due to their similarity to electrons in graphene.[13,14] The ferromagnetic spins on a 2D honeycomb lattice can be topologically nontrivial when a proper nearest neighbor exchange exists.[3] In Ref. [4], the authors investigated the properties of magnon edge states in a ferromagnetic honeycomb spin lattice with a Dzyaloshinskii–Moriya interaction (DMI). Beginning from an isotropic Heisenberg model of localized spin moments in a honeycomb lattice, Fransson et al.[5] addressed the possibility of emerging Dirac magnons. Ferreiros[7] et al. studied the influence of lattice deformations on the magnon physics of a honeycomb ferromagnet when a DMI is considered. Owerre[8] showed that the magnon Hall effect is realizable in a two-band model on the honeycomb lattice, and studied the thermal Hall conductivity. Employing the Landau–Lifshitz–Gilbert phenomenology, bulk and edge spin transport in topological magnon insulators have been studied.[9] The spin Nernst effect of magnons in a honeycomb antiferromagnet in the presence of a DMI has been demonstrated.[10,11]
Another direction that the study of topological phases has taken in recent years is manipulating the topological and transport properties of quantum systems under the influence of a periodic drive.[15–17] Changes in the band structure from a nontopological band structure to a topological one can occur. In cold atom systems, periodic changes in the laser fields establish an optical lattice potential.[18,19] In solid state systems, periodically modulated quantum systems can be effectively described by a static Hamiltonian. Therefore, magnon systems deserve consideration. In this work, we study the magnon on a honeycomb lattice with a DMI under the irradiation of light.[20–24] We study the effects of the interplay between the DMI and light.
The rest of this paper is organized as follows. In Section 2, we present the tight-binding magnon model on the honeycomb lattice. Based on the Brillouin–Wigner theory, we obtain the effective tight-binding Hamiltonian with a circularly polarized light. In Section 3, the Berry curvature and Chern number of the system are presented. In Section 3, the corresponding low-energy Dirac model is studied. Our conclusions are given in Section 5.
We consider a ferromagnetic model on a honeycomb lattice. The corresponding Hamiltonian is

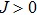


 | Fig. 1. The honeycomb lattice structure, with the nearest neighbor and the second nearest neighbors labeled by ai and di, respectively. |
Using Holstein–Primakoff transformation 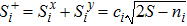
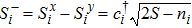
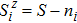
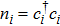
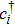

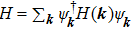

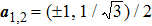




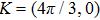

Next, we consider the effect of the circularly polarized light represented by the time-dependent vector potential
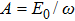
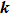




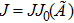
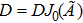


In addition,
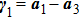


In Fig.
The Berry curvature for the n-th magnon band can be calculated from
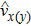
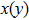





To better understand the topological properties, we present a theoretical analysis based on an effective 



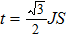


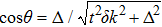
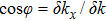


The direct correspondence between the Chern number and the Hall conductance for 2D system is characterized by 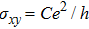




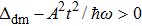
To conclude, we analyzed the topological properties of magnon in an insulator on a honeycomb lattice with DMI under the application of a circularly polarized light. We employed Brillouin–Wigner theory to obtain the tight-binding model with a circularly polarized light at the high-frequency regime. We found that the light can induce the closing and reopening of the band gap. The study about the corresponding Berry curvature and Chern number confirmed the light-induced topological phase transition. We obtained the low-energy Dirac model to better know the topological properties. The topological phase transition was light-induced handedness-dependent. The effective DMI and intrinsic DMI were responsible for the topological phase transition.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] |