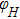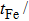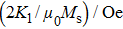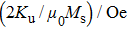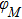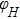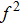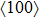† Corresponding author. E-mail:
The thickness-dependent magnetic anisotropy of obliquely deposited Fe(001)/Pd thin films on Mg(001) is investigated by fitting the field-dependent resonant field curve using the Kittel equation. In this study, three Fe film samples with thicknesses of 50 monolayers (ML), 45 ML, and 32 ML deposited at 0°, 45°, and 55°, respectively, are used. The magnetic anisotropy constant obtained from ferromagnetic resonance (FMR) spectra exhibits a dominant fourfold magnetocrystalline anisotropy (MCA) at the normal deposition angle with larger Fe thickness. However, the in-plane uniaxial magnetic anisotropy (UMA) is induced by a higher oblique deposition angle and a smaller thickness. Its hard axis lies between the [100] and [010] directions. The FMR data-fitting analysis yields a precise measurement of smaller contributions to the magnetic anisotropy, such as in-plane UMA. Due to MCA, when the magnetic field is weaker than the saturated field, the magnetization direction does not always align with the external field. The squared frequency-dependent resonant field measurement gives an isotropic Landé g-factor of 2.07. Our results are consistent with previous experiments conducted on the magneto-optical Kerr effect (MOKE) and anisotropic magnetoresistance (AMR) systems. Thus, a vector network analyzer ferromagnetic resonance (VNA-FMR) test-method for finding UMA in obliquely deposited Fe(001)/Pd bilayer ferromagnetic thin films, and determining the magnetic anisotropy constants with respect to the film normal deposition, is proposed.
Ferromagnetic thin films can exhibit extensively modified magnetic properties from their bulk counterparts,[1] including magnetic anisotropy, magnetic homogeneity, and intrinsic magnetic damping properties,[2] thus they have potential applications in microscale actuators and sensors, magnetic recording media components,[3] current-induced magnetization switching devices,[4] and high-density magnetic random access memory.[5] It is not easy to use conventional tools to determine the magnetic anisotropy that controls the operation of these films. The ferromagnetic resonance (FMR) technique is a very sensitive tool for studying the magnetic anisotropy, spin dynamics, and homogeneity of ferromagnetic thin films.
Magnetic anisotropy is one of the basic properties of ferromagnetic materials. In general, there are several ways to enhance in-plane uniaxial magnetic anisotropy (UMA) in ferromagnetic films, such as oblique deposition,[6–8] magnetic annealing,[9–13] and exchange bias.[14–18] Among these, oblique deposition is easy to handle and thus is widely used in practice to increase the ferromagnetic resonance frequency of ferromagnetic thin films.[19,20] Due to the self-shadowing effect, the oblique deposition of ferromagnetic thin films on flat rigid substrates can result in elongated grains perpendicular to the direction of the incident atomic flux. Therefore, during the growth of the ferromagnetic film, UMA with an easy axis perpendicular to the direction of the incident flux is induced.[21]
For decades, FMR has been one of the most effective techniques to determine the crystallinity of ferromagnetic materials and to measure the phenomenological magnetic anisotropy constants. With the increasing interest in research on ferromagnetic thin films, FMR has been used more and more in research into single crystal ferromagnetic thin films.[22–27] The FMR technique has also proven to be a powerful technique for measuring the magnetic properties of oblique anisotropic films.[2] At gigahertz (GHz), FMR accurately measures the static characteristics of large magnetic field saturated magnetic films.[28–30] In these experiments, magnetic resonance was detected by scanning an applied magnetic field. The resonant magnetic field provides a measure of the effective field excited by a uniform magnetic field in a uniform precession mode. The effective field includes contributions from external magnetic fields, demagnetizing fields, and magnetocrystalline energy. The standard FMR technique provides very high sensitivity because the high-quality coefficient of the cavity at the operating frequency is determined by the geometry of the cavity. It is proved that this method can accurately measure the static characteristics of a ferromagnetic film, which are given by the magnetic anisotropy constant. The dynamic characteristics are usually determined by the resonance linewidth 
In this paper, we focus on the static properties of epitaxial Fe(001)/Pd thin film bilayers, which are highly attractive due to the increased switching speed of the magnetic cells in magnetic random access memory (M-RAM) devices.[32,33] In previous studies on similar Fe/MgO(001) thin films with fourfold magnetocrystalline anisotropy (MCA) and a UMA superimposed, the latter is very likely to be along an easy direction, that is, β = 0° or 90°. It is reported that at small Fe thickness, the uniaxial component dominates, and as the thickness increases, the relative anisotropy of cubic anisotropy increases. Therefore, controlling uniaxial anisotropy is important because it facilitates device applications such as magnetic tunnel junctions and spin torque oscillators.[34] In this work, we present results of thickness-dependent magnetic anisotropy of obliquely deposited Fe(001)/Pd thin films on Mg(001) via field-dependent resonant field measurements. Our experimental results are compared with the previous ones obtained from the quasistatic transverse biased inverse susceptibility (TBIS) measurements,[28,35] and high-frequency FMR measurements,[28] as well as the magneto-optical Kerr effect (MOKE) and anisotropic magnetoresistance (AMR) systems,[36] which indicates that in addition to the fourfold MCA due to the body-center cubic (bcc) structure of Fe, an additional UMA is found in the [100] easy direction.
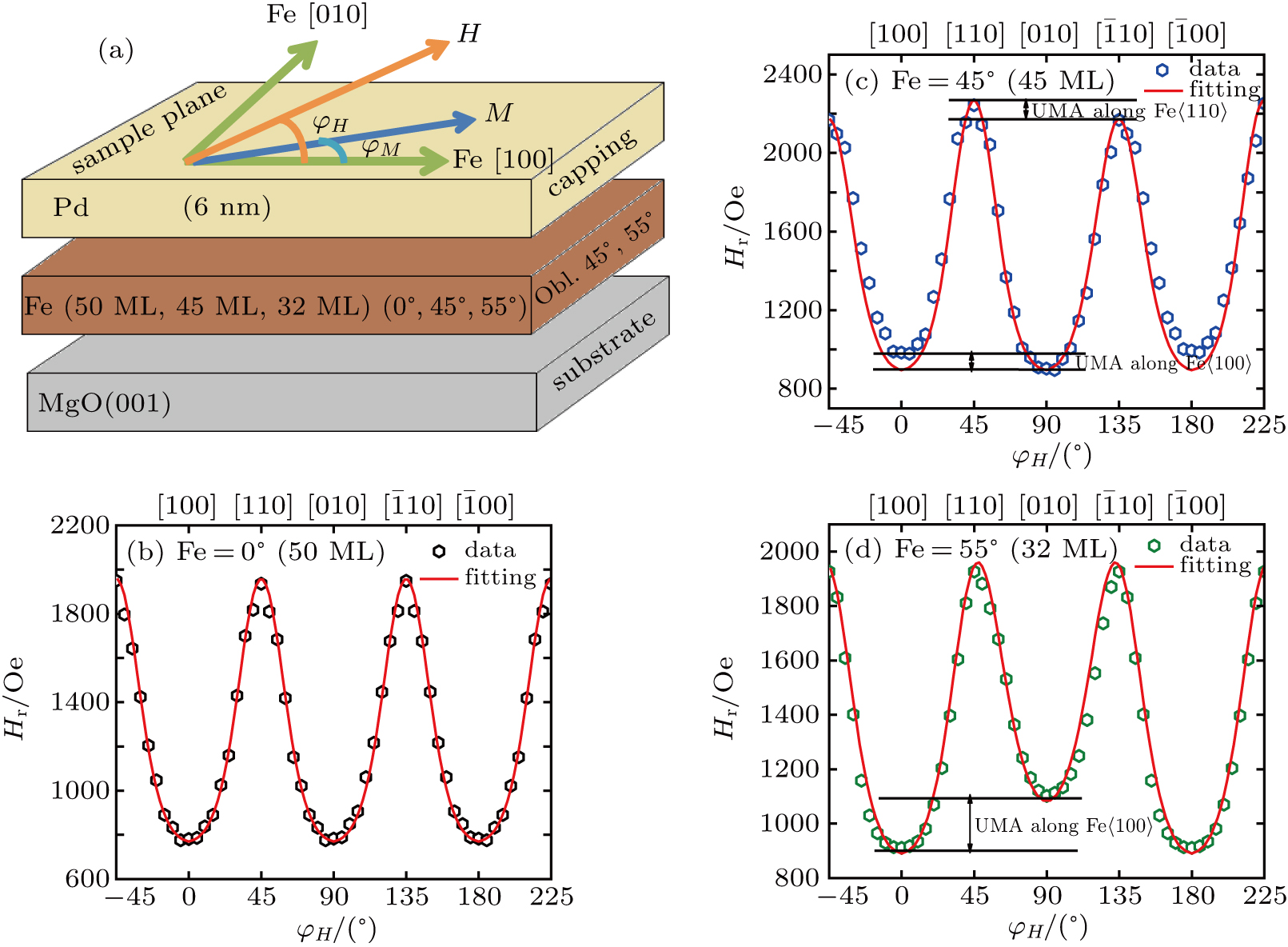
Using ultra-high vacuum (UHV) molecular beam epitaxy, thin magnetic films of Fe(001)/Pd bilayers were prepared on cleaned MgO(001) substrates via oblique deposition at a base pressure of 2.0 ×10−10 mbar. The substrates were put into a special template-holder and were heated up to 700 °C for 2 h. Our previous study showed that this temperature range is the best choice for producing high quality samples. Detailed information on sample preparation and characterization has been provided elsewhere.[36] In this paper, three samples of Fe film thicknesses 50 monolayer (ML), 45 ML, and 32 ML, which were 0° normally, and 45°, and 55° obliquely deposited, respectively, were adopted for the study. The magnetic anisotropy was analyzed using an in-plane vector network analyzer ferromagnetic resonance (VNA-FMR) technique. The measurements were performed by placing the samples with film side facing the coplanar waveguide (CPW) at room temperature. A gaussmeter was used to measure the magnetic field at each field. Microwave excitations were generated by connecting one end of the CPW to the output port of the vector network analyzer (VNA). The input port of the VNA was connected to the other end of the CPW, and the complex transmission parameter S21 through the CPW was measured at a fixed frequency as the external magnetic field was swept.[37] The field-dependent resonant field measurements were performed by rotating the sample in-plane while sweeping the applied magnetic field.
Figure 
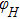
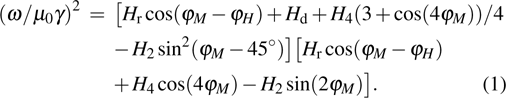 |

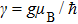

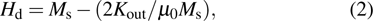 |
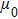

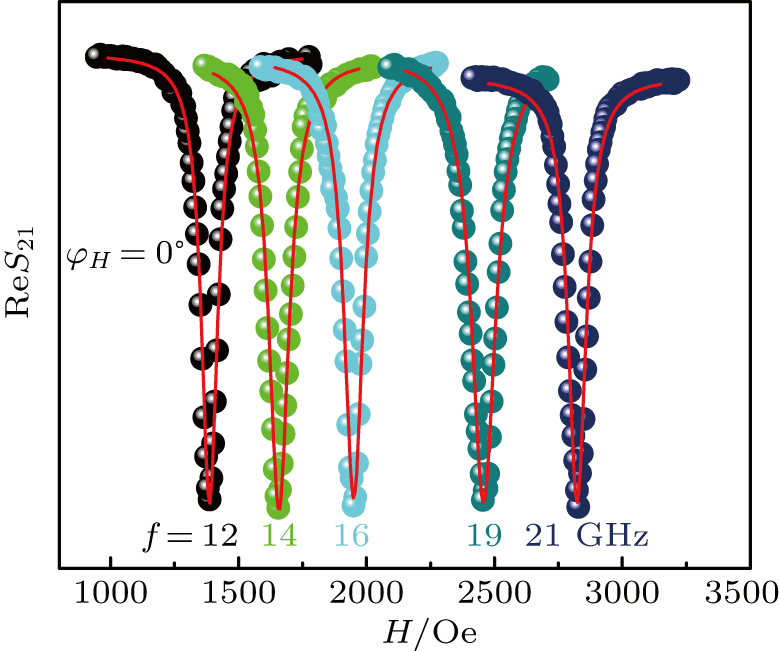 | Fig. 2. FMR spectra (fitted red lines) of the 0°-Fe(50 ML)/Pd sample at 
|
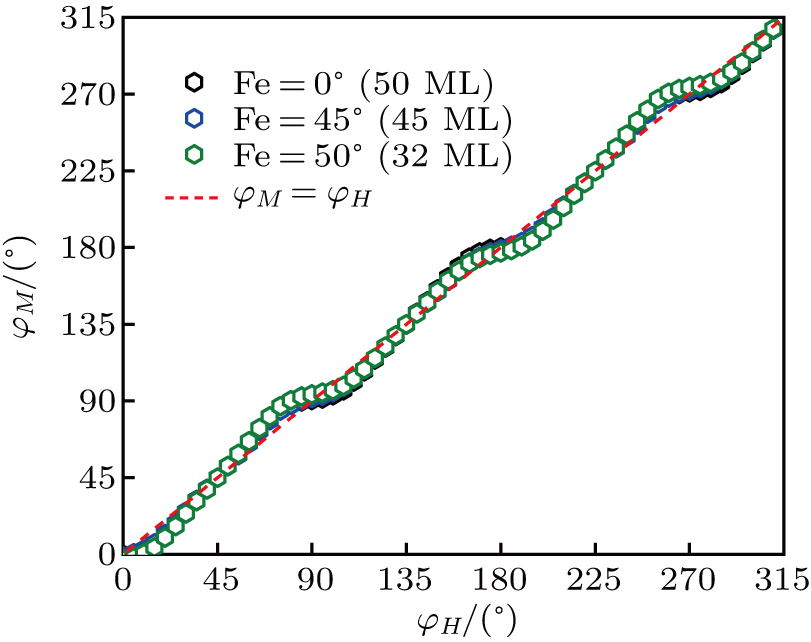
We also evaluate the equilibrium magnetization angle 
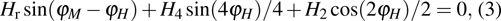 |
For the special case where the magnetic field is oriented along the [100]-easy or [110]-hard direction and the in-plane uniaxial term is ignored, equation (
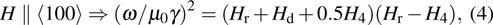 |
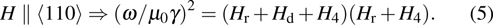 |
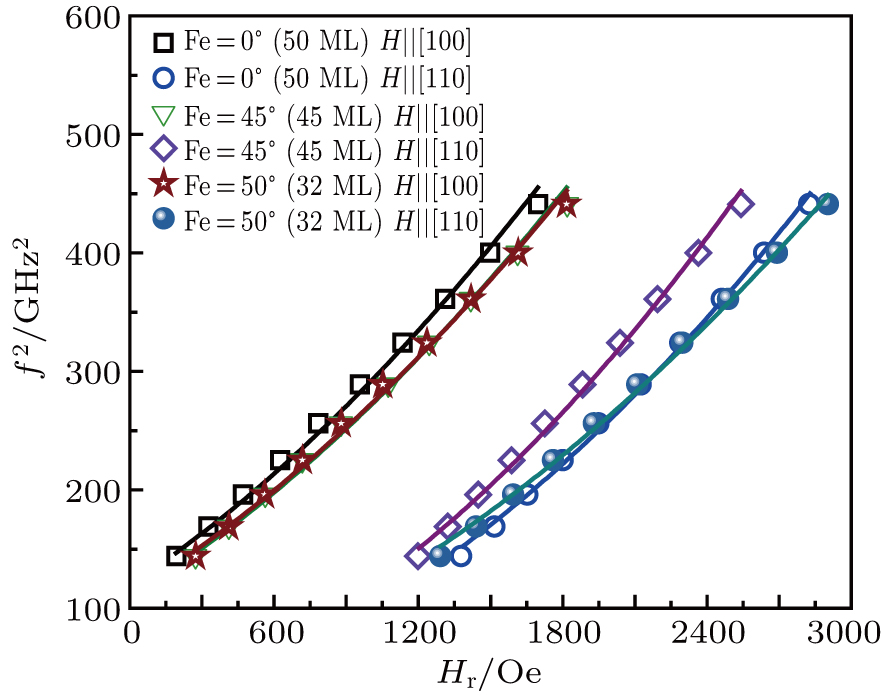
In order to evaluate the magnetic anisotropy constants, the field-dependent resonant field measurement via the Kittel equation was performed at a fixed frequency. The experimental data are fitted with Eq. (
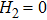
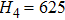
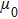
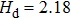

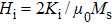
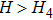
| Table 1.
Summarized magnetic parameters of Fe(001)/Pd thin films with different Fe-thicknesses and deposition angles. The error bars of the magnetic anisotropy field terms are 10% and are mainly given by the uncertainty of the sample volume. . |
Note that the resonance field Hr around the [100] easy axis changes more slowly with angle than that around the [110] hard axis. This behavior may be caused by dragging the saturation magnetization behind the external magnetic field due to a strong in-plane fourfold MCA. In general, dragging enhances the damping and only drags along the easy and hard axes of magnetization, but where M and H are parallel, the dragging contribution vanishes. Figure 

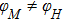
Figure 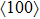

We study the thickness-dependent magnetic anisotropy of obliquely deposited Fe(001)/Pd thin film bilayer samples using the VNA-FMR technique. The magnetic anisotropy constants are obtained by fitting the field-dependent resonant field curves at 16 GHz using the Kittel equation. Though the normally deposited sample does not show an intrinsic UMA, it is reported that oblique deposition could cause in-plane UMA. A consequence of this is that an FMR data-fitting analysis yields precise measurement of smaller contributions to the magnetic anisotropy, such as in-plane UMA. This UMA is inferred to be the shadow effect of the evaporation flux rate deviating from the normal incidence. This study shows that the magnetic anisotropy of the Pd/Fe(001)/Mg(001) system can be modified via oblique deposition, opening up a way to control the magnetic anisotropy, which might be significant for the switching of spintronic devices. The oblique deposition method may be applicable to other systems composed of two or more elements and can be of interest in the application because the crystal quality and magnetostatic parameters are not affected by changing the growth conditions and, furthermore, the film interfaces are not involved in this procedure.[29]
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] |