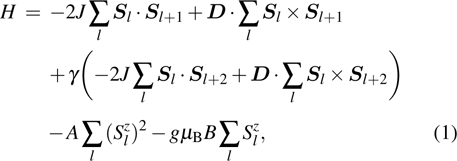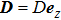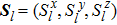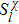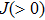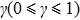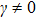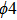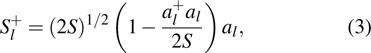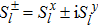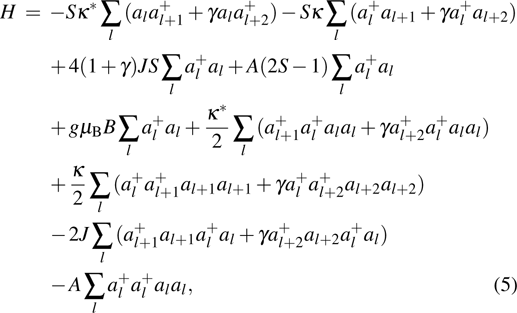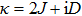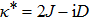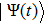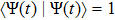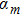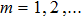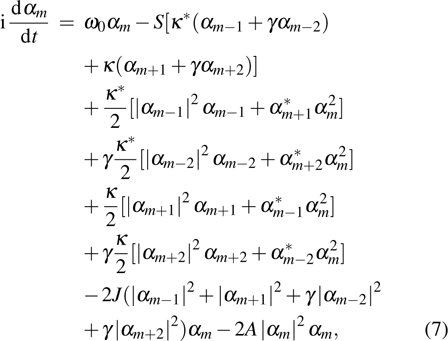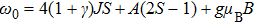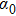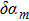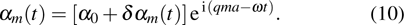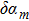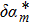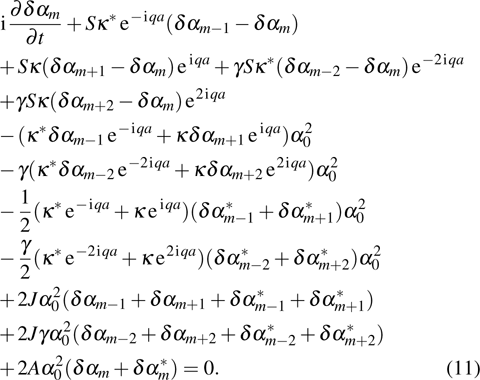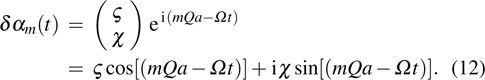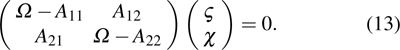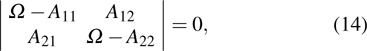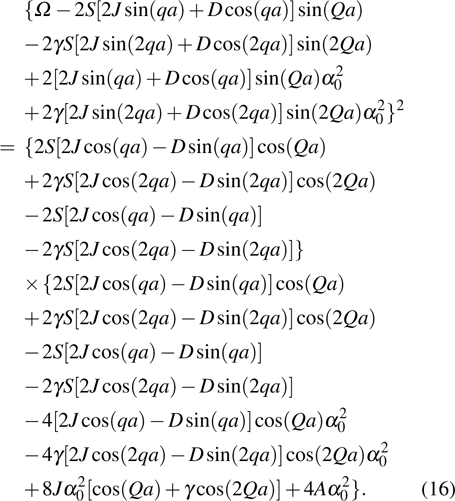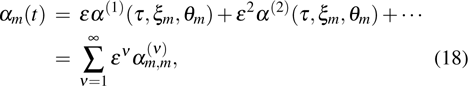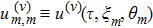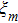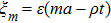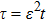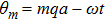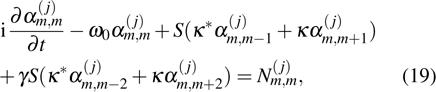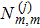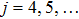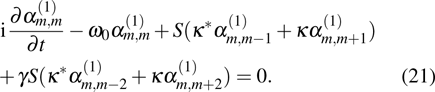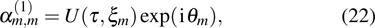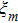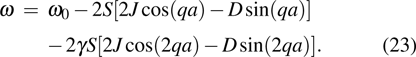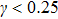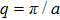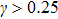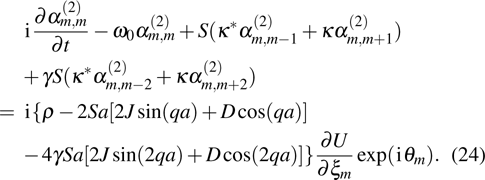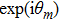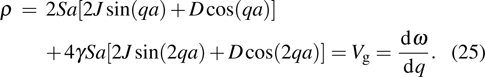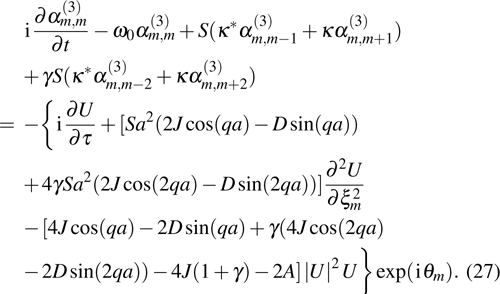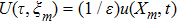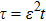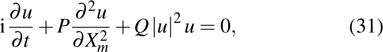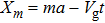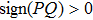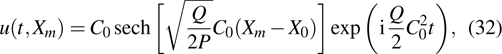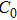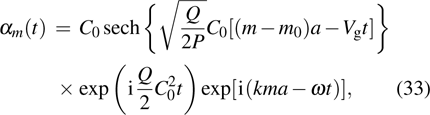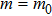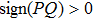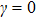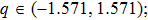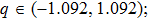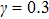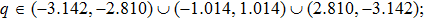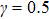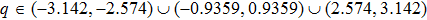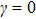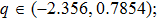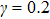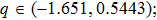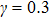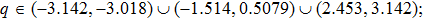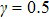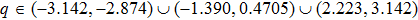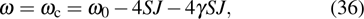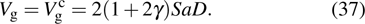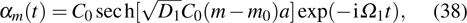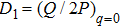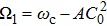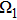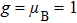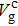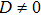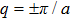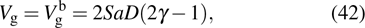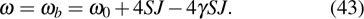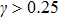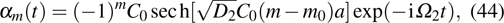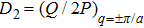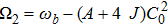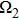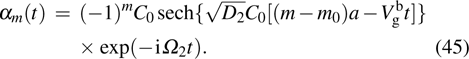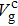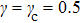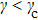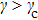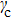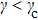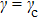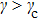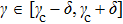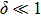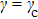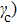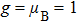Cite this Article
Xie Jiayu, Deng Zhihao, Chang Xia, Tang Bing. Discrete modulational instability and bright localized spin wave modes in easy-axis weak ferromagnetic spin chains involving the next-nearest-neighbor coupling. Chinese Physics B, 2019, 28(7): 077501  
Permissions
Discrete modulational instability and bright localized spin wave modes in easy-axis weak ferromagnetic spin chains involving the next-nearest-neighbor coupling
Xie Jiayu1, Deng Zhihao1, Chang Xia1, Tang Bing1, 2, †
College of Physics, Mechanical and Electrical Engineering, Jishou University, Jishou 416000, China
The Collaborative Innovation Center of Manganese–Zinc–Vanadium Industrial Technology, Jishou University, Jishou 416000, China

 

† Corresponding author. E-mail: bingtangphy@jsu.edu.cn

Abstract

We report a theoretical work on the properties of modulational instability and bright type nonlinear localized modes in one-dimensional easy-axis weak ferromagnetic spin lattices involving next-nearest-neighbor couplings. With a linear stability analysis, we calculate the growth rates of the modulational instability, and plot the instability regions. When the strength of the next-nearest-neighbor coupling is large enough, two new asymmetric modulational instability regions appear near the boundary of the first Brillouin zone. Furthermore, analytical forms of the bright nonlinear localized modes are constructed by means of a quasi-discreteness approach. The influence of the next-nearest-neighbor coupling on the Brillouin zone center mode and boundary mode are discussed. In particular, we discover a reversal phenomenon of the propagation direction of the Brillouin zone boundary mode.

PACS: 75.10.Jm;75.30.Ds;63.20.Pw
Keyword:modulational instability analysis;intrinsic localized spin-wave modes;weak ferromagnets;next-nearest-neighbor couplings
1. Introduction

Modulational instability is a common nonlinear process, which can appear in various fields of physics.[1–8] The modulational instability is characterized by an exponential growth of arbitrarily amplitude perturbations on account of the interplay between dispersion (or diffraction) and nonlinearity.[9] Theoretically, a particular region of wave numbers of the plane wave configurations becomes unstable to modulations due to the modulational instability, which leads to the rapid growth of the unstable modes and eventually to localization in configuration space. In nonlinear systems, the modulational instability is of crucial significance for creating localized excitations, such as bright solitons,[10–13] breathers,[14,15] and rogue waves.[16] In general, the modulational instability is a vital characteristic of continuum and discrete nonlinear systems. Up to now, modulational instabilities have been identified in many real physical systems, including electrical transmission line, discrete optical nonlinear arrays, Bose–Einstein condensates, and so on.[17–19]

The character and the significance of modulational instabilities of plane waves in the dynamics behavior of nonlinear lattice systems have been extensively investigated.[20–25] In many published works, modulational instabilities of plane waves were studied in the context of different types of discrete nonlinear Schrödinger equations, which are often used to describe the dynamics of nonlinear lattices. The modulational instability is identified as the first step to localization in discrete nonlinear systems.[23] For discrete nonlinear systems, the instability rapid growth brings about a relaxation process upon the energy equipartition, which causes the formation of localized modes.[24] Generally, the bright nonlinear localized mode appears in the parameter range in which the discrete nonlinear lattice reveals modulational instability.[21]

The spin chain model is a typical nonlinear lattice system. In spin chains, the modulated spin plan waves may develop into nonlinear localized modes when the instability is completely evolved. Naturally, this lattice model provides a good stage to exhibit modulational instability and nonlinear localized modes.[26] Lai and Sievers pointed out that the formation of the localized spin excitations comes from extended spin waves via the discrete modulational instability.[27] From their point of view, both discreteness and strong nonlinearity may be fundamental for the generation of the stable spin localized mode. Until now, much attention has been focused on the research of discrete modulational instability and localized spin wave modes in one-dimensional ferromagnetic spin lattices.[28–34] In our previous work, we found that the discrete modulational instability of the q = 0 plane spin wave occurs in the easy-axis anisotropy ferromagnetic spin lattice.[33] This finding suggests that a localized spin wave mode with bright construction can exist at the Brillouin zone center. Moreover, Nguenang et al. proposed several new characteristics of localized spin wave modes in an easy-plane ferromagnetic spin lattice with biquadratic isotropic exchange interaction by analyzing the discrete modulational instability of spin plan waves.[30] Lately, Kavitha et al. studied discrete modulational instability and localized spin wave modes in an easy-axis weak ferromagnetic spin lattice chain only with nearest-neighbor couplings.[34] They showed that the Dzyaloshinsky–Moriya (DM) interaction can evidently influence nonlinear localized spin wave modes, and this ferromagnetic spin lattice with the DM interaction supports the stable localized spin wave mode. It is well-known that the DM interaction was put forward by Dzyaloshinsky[31] and Moriya[32] to characterize weak ferromagnetism in magnets. Furthermore, many researchers found that the appearance of the Dzyaloshinsky–Moriya interaction can cause many interesting physical effects,[37–42] such as the asymmetry of the magnon dispersion relation,[38] the creation of a unidirectional spin-wave emission,[41] and the asymmetric magnetic domain-wall motion.[42]

In this study, we analytically investigate the modulational instability and localized spin wave modes with bright-profile in a one-dimensional easy-axis weak ferromagnetic spin lattice with the nearest-neighbor (NN) coupling and the next-nearest-neighbor (NNN) coupling in the semiclassical limit. The main aim of this theoretical study is to explore the influence of next-nearest-neighbor couplings on the properties of discrete modulational instability and bright localized spin wave modes in weak ferromagnets. The framework of the paper is as follows. In Section 2, we expound the present weak ferromagnetic lattice model and drive the corresponding equation of motion in the Glauber state representation. In Section 3, the discrete modulational instability in our weak ferromagnetic spin lattice is analyzed via the linear stability analysis. We also forecast the parameter regions for the existence of bright type localized modes. In Section 4, taking advantage of a quasi-discreteness approach, we obtain analytical forms of the bright nonlinear localized modes and analyze their existence condition. In particular, both the bright Brillouin zone center mode and boundary mode are achieved. The last section is devoted to summarizing our work.

2. The spin lattice model and equation of motion

In this research, we focus our attention on an easy-axis anisotropy weak ferromagnetic lattice model with NN and NNN couplings. The Hamiltonian for the system under an external magnetic field can be written in the following form:

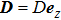
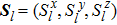
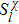
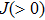
with and , where is the χ component of the local spin operator on lattice site l, corresponds to the NN exchange coupling parameter, A is a crystal field uniaxial anisotropy parameter, D stands for the intensity of the NN DM interaction, and B denotes the intensity of the external magnetic field along the z direction. Obviously, the ground-state profile of the weak ferromagnetic chain system corresponds to all local spins aligned along with the external magnetic field. 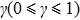The main characteristic of the weak ferromagnetic lattice system is that the coefficient is variable, which manages the relative intensity of the NNN interactions to the NN interactions. A special case of γ =0 corresponds to the usual weak ferromagnetic chains with NN interactions only. 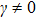For a general case of , we then propose the weak ferromagnetic chains involving the NNN interactions. In our previous works, the other lattice models involving the NNN interactions have been considered. In Ref. [43], we have studied modulational instability and discrete breathers in a nonlinear helicoidal lattice model, which is motivated by a helicoidal optical lattice for ultracold atoms. By using the semidiscrete multiple-scale method, we have obtained analytical solutions of discrete breather modes in this helicoidal lattice with different types of nonlinearities. In Ref. 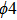[44], we have investigated discrete breathers and modulational instability in a one-dimensional lattice with the NNN coupling interaction, which is a pure classical lattice model. The evident difference from these two lattice models is that the present weak ferromagnetic chain contains the DM interaction, which is antisymmetric. Physically, some new effects may occur when the weak ferromagnetic chain has the NNN exchange coupling interaction and the NNN DM interaction.

To obtain the second quantized expression of the Hamiltonian for the weak ferromagnetic lattice system, we can take advantage of the Dyson–Maleev transformation[45,46] for all local spin operators

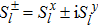
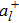
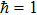
with , where al ( ) corresponds to the local magnon annihilation (creation) operator in the l-th lattice site, and S is the absolute value of the spin magnitude. For simplicity, the Planck constant is set to throughout the paper. The substitution of Eqs. (2)–(4) into the Hamiltonian (1) yields a bosonlized Hamiltonian, which reads
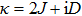
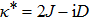
with and . In this equation, the zero-point energy of the weak ferromagnetic chain system has been abandoned.

To characterize the constituents of the quantum state corresponding to the weak ferromagnetic spin chain system, one may adopt the Glauber coherent-state 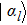[47] as a basic representation of the present spin lattice chain. Thus, the quantum state for the weak ferromagnetic lattice 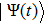can be written in a product of the form

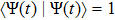
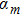
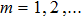
with . Theoretically, we can make use of the Ehrenfest theorem so as to obtain the equation of motion for the expectation of the Hermitian operator.[48] After carrying out some mathematical derivations, one may obtain equations of motion corresponding to the coherent-state amplitude ( ), namely,
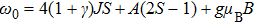
with . It is obvious that the discreteness and nonlinearity effects in the weak ferromagnetic spin chain that we consider are completely involved in Eq. (7).

3. Discrete modulational instability analysis

Theoretically, the presence of the bright type nonlinear spin wave localized mode is associated with the discrete modulational instability of the spin plane wave. Hence, the discrete modulational instability of Eq. (7) will be investigated by using a linear stability analysis.[49] Let us start to do the linear stability analysis by seeking discrete plane wave solutions of Eq. (7), which is

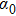
where is an invariable amplitude, q represents the wave number of discrete plane waves, a corresponds to the lattice constant, and ω denotes the circular frequency of the discrete plane-wave. The insertion of the discrete plane wave solutions (8) into the equation of motion (7) leads to a nonlinear dispersion relation, which reads

Next, we introduce a small perturbation 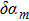in Eq. (8) and suppose that the solution of Eq. (7) is

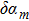
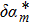
By inserting the above solution (10) in Eq. (7) and keeping those linear terms for the perturbations and , we obtain a linear differential equation
In the light of the process of the linear stability analysis, we need to suppose that the above equation has the following general solution:[50]
Here, Q and Ω are, respectively, the wave number and the circular frequency corresponding to the small disturbance amplitude. Moreover, ς and χ denote two arbitrary real variables. Substituting the general solution (12) into Eq. (11), then we have
The condition for Eq. (13) with untrivial solutions is given by the second order equation for the perturbation frequency Ω, i.e.,
with
After carrying out a simple derivation, equation (14) can be rewritten as

The discrete plane spin wave solution (8) is thought to be modulationally unstable when the right-hand side part of Eq. (16) is negative.[51] In the present physical scenario, the growth rate of the modulational instability can be expressed as

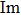
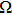
where denotes the imaginary part of the perturbation circular frequency . If the modulational instability of the discrete spin plane wave takes place, then the bright localized solution to the equation of motion (7) can exist. Here, we will consider two cases: without the DM interaction and with the DM interaction. Our goal is to study the influence of the NNN couplings on modulational instability regions in the two cases. Moreover, considering that the easy-axis anisotropy is quite crucial for the presence of the bright Brillouin zone center mode in the ferromagnetic spin chain system, the value of the easy-axis anisotropy parameter will be large enough in the analysis that follows.

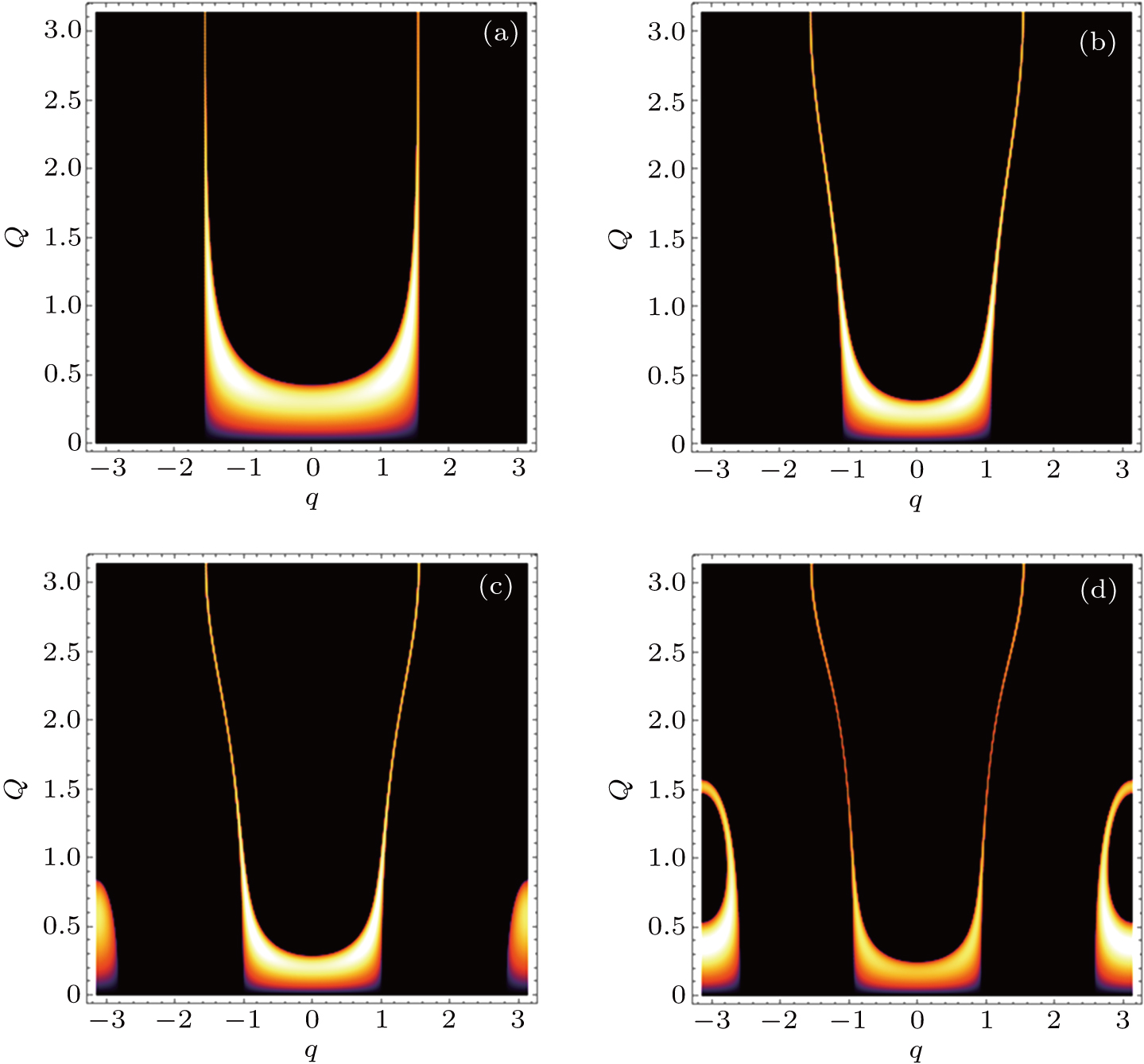
First, let us discuss the case of D = 0; i.e., the absence of the DM interaction. In Fig. 1, we plot the area (white) of discrete modulational instability on plane (q,Q) for the corresponding easy-axis ferromagnetic chain with different relative coupling strengths γ. In Fig. 1, we can directly see that the form of the area of the discrete modulational instability varies remarkably with the increase of γ. In particular, new modulational instability regions arise near the first Brillouin zone edge once γ is sufficiently large. It is obvious that the q = 0 spin plane waves are always modulationally unstable near the perturbation wave number Q = 0 with the increase of γ. Physically, the occurrence of the discrete modulational instability means that the spin lattice chain system supports the bright type localized spin wave mode in the corresponding parameter regions.

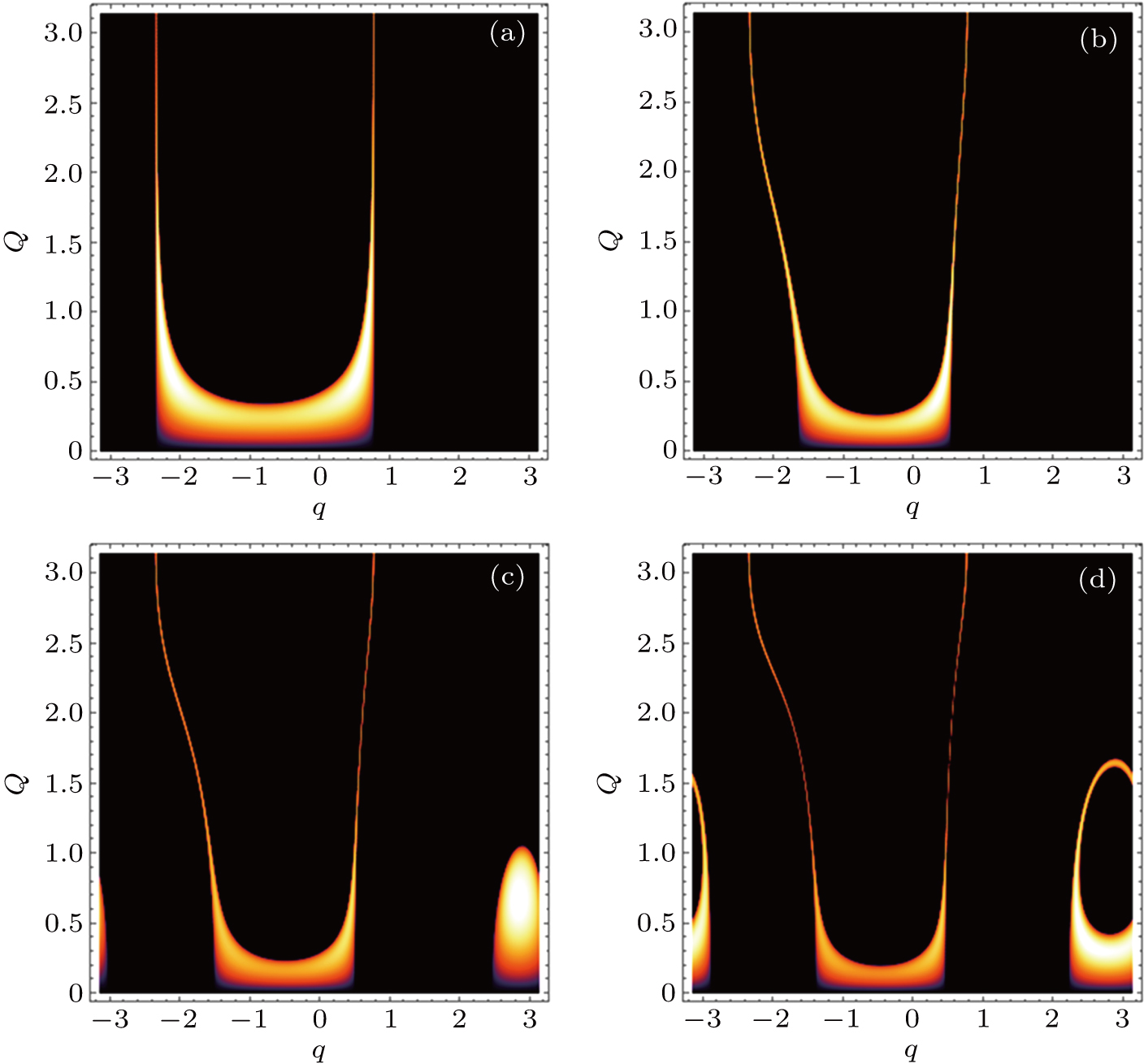
Fig. 1. Modulational instability regions (bright zone) on the (q,Q) plane for different values of γ: (a) 0, (b) 0.2, (c) 0.3, (d) 0.5. The relevant parameters include D = 0, J = 1, S = 10, a = 1, A = 10, and .

Next, we consider the case of the presence of the DM interaction. In Fig. 2, we present the corresponding modulational instability region in plane (q,Q) for different strengths of NNN couplings. Compared with Fig. 1, we clearly see that the modulational instability areas shift to the left-hand side of the first Brillouin zone because of the introduction of the DM interaction. Physically, the emergence of this effect is due to the antisymmetric property of the DM interaction. In Fig. 2, one also can observe the effect of the increase of NNN couplings on the configuration of the modulational instability regions for the weak ferromagnetic chain. We note that two asymmetric modulational instability regions appear in the left-hand and right-hand edges of the first Brillouin zone when γ is large enough.

Fig. 2. Modulational instability regions (bright zone) on the (q,Q) plane for different values of γ: (a) 0, (b) 0.2, (c) 0.3, (d) 0.5. The relevant parameters are set to D = 2, J = 1, S = 10, a = 1, A = 10, and .
4. Nonlinear localized modes
4.1. Reduction of the equation of motion

In the present study, we shall employ a quasi-discreteness approach[52] to study the effects of nonlinearity and discreteness of the weak ferromagnetic chains involving the NNN interactions. By means of this quasi-discreteness technique, one can look for the analytical expression of the nonlinear localized mode in nonlinear lattice systems. In the quasi-discreteness approach, we first need to expand the coherent-state amplitude 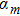in terms of the small coefficient ε, namely,

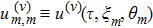
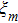
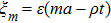
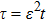
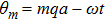
with . Here, and τ correspond to the multiple-scales mathematical variables that are given by and , respectively. Actually, ρ stands for the group velocity of the carrier wave, which shall be demonstrated by taking advantage of a solvability condition. signifies the phase of those carrier waves. In addition, a corresponds to the lattice constant of the present weak ferromagnetic chain; q and ω are, respectively, the corresponding wave number and circular frequency. After inserting Eq. (18) into Eq. (7), we then obtain
with
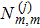
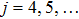
which can be solved analytically by making use of the step by step procedure. It should be pointed out that the detailed expressions of terms ( ) are not written in this equation for simplicity. First, let us consider the first-order approximation (j = 1), one then obtain the linear wave equation
Evidently, the above equation exists the following solution:
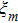
where U is the envelope function of τ and . This can be determined in the following derivations. By inserting the solution (22) into Eq. (21), it is easy to obtain the dispersion relation of the linear spin waves, which is

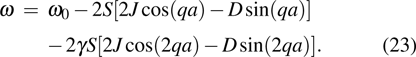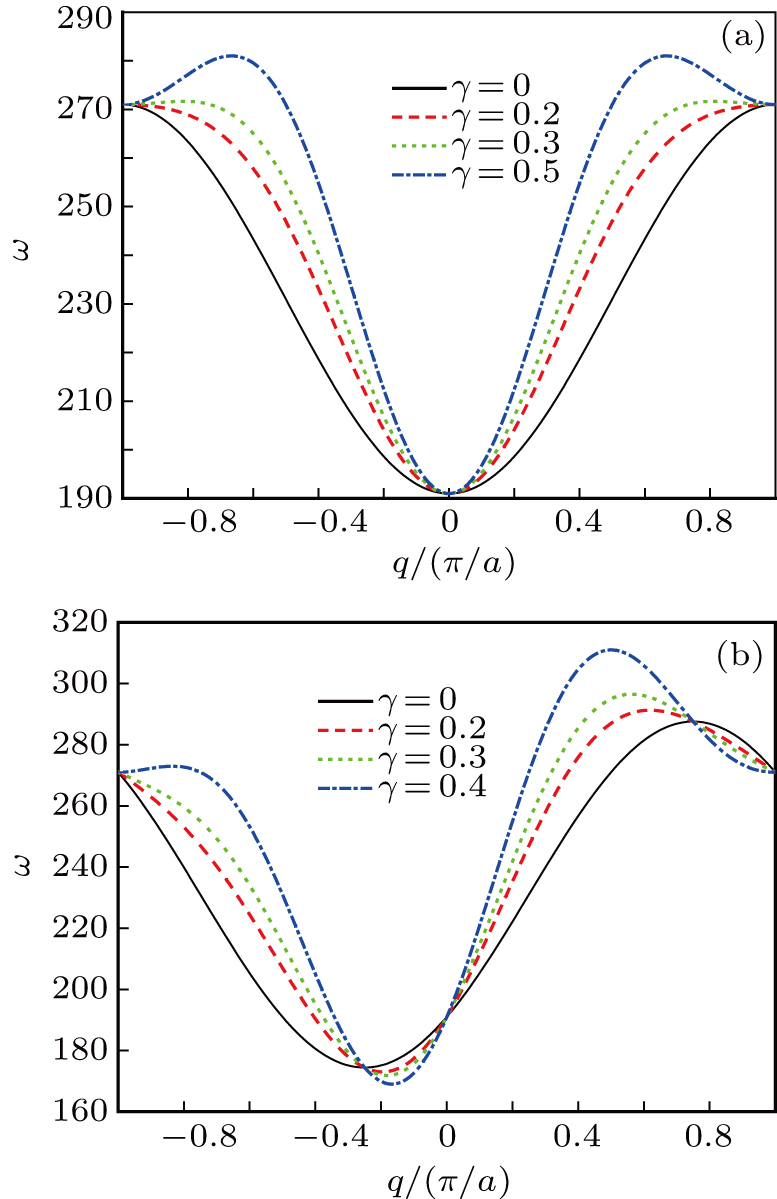
In Fig. 3, we plot the magnon dispersion curves of the present ferromagnetic chain system for different values of the relative next-nearest-neighbor coupling intensity γ. Figures 3(a) and 3(b) correspond to the ferromagnetic chain without and with the DM interaction, respectively. We can clearly see that the increase of the relative next-nearest-neighbor coupling constant can affect the shape of the magnon dispersion curve significantly. When the DM interaction is absent, from Eq. (23) we can give the following exact results: (i) for the cases of 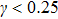, the magnon frequency has a minimum value at q = 0 and a maximum value at 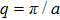; (ii) for the cases of 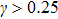, a new maximum arises at wave number . These results are visually presented in Fig. 3(a). The effect of the DM interaction on the magnon dispersion curves can be observed by comparing Fig. 3(a) with Fig. 3(b). It is not hard to find that the introduction of the DM interaction causes that the magnon dispersion curves shift to the left end of the first Brillouin zone. Moreover, in Fig. 3(b), it is clearly see that the extreme points of the magnon frequency move left in the first Brillouin zone with increasing γ.

Fig. 3. The magnon dispersion curves of the present ferromagnetic chain system with different values of γ: (a) D = 0, (b) D = 2. The other parameters are set to J = 1, S = 10, a = 1, A = 10, , and B = 1.

Next, we analyze the second-order approximation (j=2). After doing a simple calculation, one has

On the basis of the perturbation approach, those terms proportional to 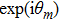in Eq. (24) should be equal to zero. Hence, we can obtain the following relation:

In the above equation, ρ has been certified to be equal to the group velocity. Making use of the solvability condition (25), one can obtain a particular solution to Eq. (24), which has the following form:
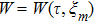
Here, is still an uncertain envelope function. In principle, it can be determined in higher-order approximations. However, from the standard procedure of the quasi-discreteness approach,[29,56] we do not need to consider this process.

Now, we pay attention to the case of j = 3 in Eq. (19). With the help of the obtained results, one can obtain the following equation:

To make sure that the perturbation theory is reasonable, these secular terms in the above equation must disappear. Consequently, we have

with
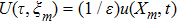
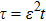
Introducing the functional transformation and utilizing , one can rewrite Eq. (28) in the form
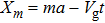
where . Evidently, equation (31) is a general (cubic) nonlinear Schrödinger equation (NLSE). In general, the NLSE is totally integrable. Its solutions, such as soliton, breather, and rogue wave, can be constructed via the inverse scattering method,[53] the Hirota bilinearization method,[54,55] and the Darboux transformation.[56,57]

4.2. Bright soliton modes

Since we mainly focus on the bright type localized spin wave modes in the easy-axis weak ferromagnetic chain, we need to consider the bright soliton solution of the NLSE. Theoretically, only when P and Q satisfy 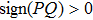, equation (31) has the bright soliton solution, which is

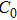
where corresponds to the bright soliton amplitude and X0 denotes the corresponding initial position. After performing some simple derivation, we have
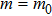
which is obviously a bright (discrete) soliton mode of the easy-axis weak ferromagnetic spin lattice chain. The central position of this nonlinear localized mode is at site , which is linked to the original excitation situation of the lattice chain system.

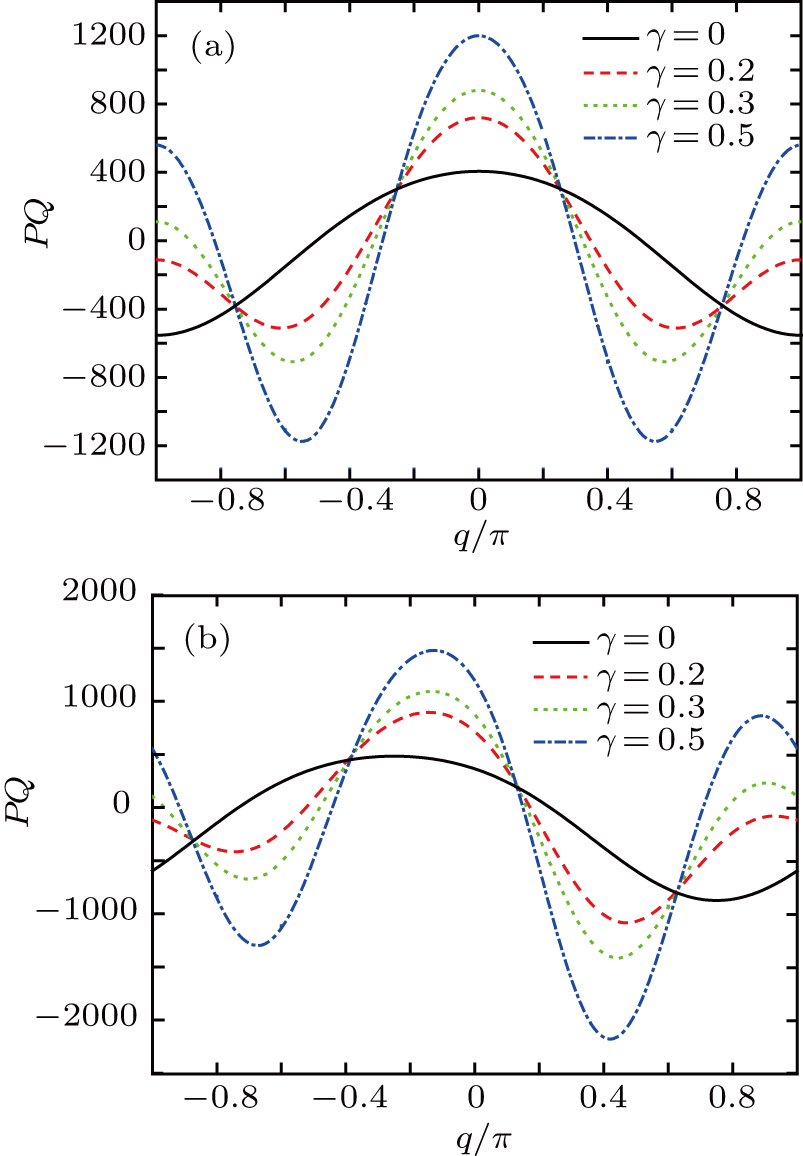
In Section 3, we have predicted the wave number region corresponding to the emergence of the bright nonlinear localized mode by the discrete modulational instability analysis. Here, from Eqs. (29) and (30) one can directly confirm that the bright type nonlinear localized spin wave mode appears in a specific wave number region, in which P and Q must follow 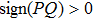. In Fig. 4, we display the product PQ function curves with wave number q under different values of γ. Figure 4(a) and 4(b) correspond to the cases of the ferromagnetic chain without and with the DM interaction, respectively. For Fig. 4(a), we can calculate the wave number regions that obey :

Fig. 4. The product PQ versus the wave number q for different values of γ: (a) without the DM interaction; (b) in the presence of the DM interaction. The used system parameters in the two figures are the same as those in Figs. 1 and 2, respectively.

(i) ,

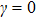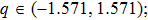
(ii) ,

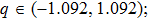
(iii) ,

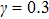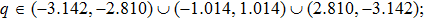
(iv) , .

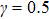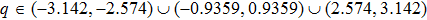Similarly, for Fig. 4(b), we can also give the corresponding wave number regions:

(i) ,

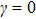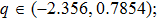
(ii) ,

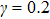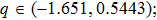
(iii) ,

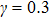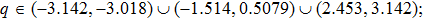
(iv) , .

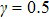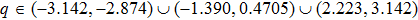We find that these results agree well with Figs. 1 and 2, respectively. That is to say, our predictions based on the discrete modulational instability analysis are responsible.

In the following, we will consider two special nonlinear modes, i.e., the Brillouin zone center mode and boundary mode. We expect that the bright nonlinear localized modes may appear at the Brillouin zone center or boundary. Furthermore, for the present easy-axis weak ferromagnetic chain, the introduction of NNN couplings may lead to new features of these modes.

4.3. Brillouin zone center mode

At the center of the first Brillouin zone q = 0, one has

In the absence of the DM interaction, the Brillouin zone center mode is obviously a stationary intrinsic localized spin wave mode (or spin discrete breather) with bright-type structure that can be written as
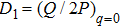
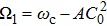
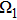
with and . Here, is the eigen-frequency of the Brillouin zone center mode, which is below the base of the linear spin wave frequency band. The temporal evolution (3D figures) corresponding to the square modulus of the coherent state amplitude for our Brillouin zone center mode (38) is displayed in Fig. 5(a). From Fig. 5(a), we clearly see a stationary bright localized structure.

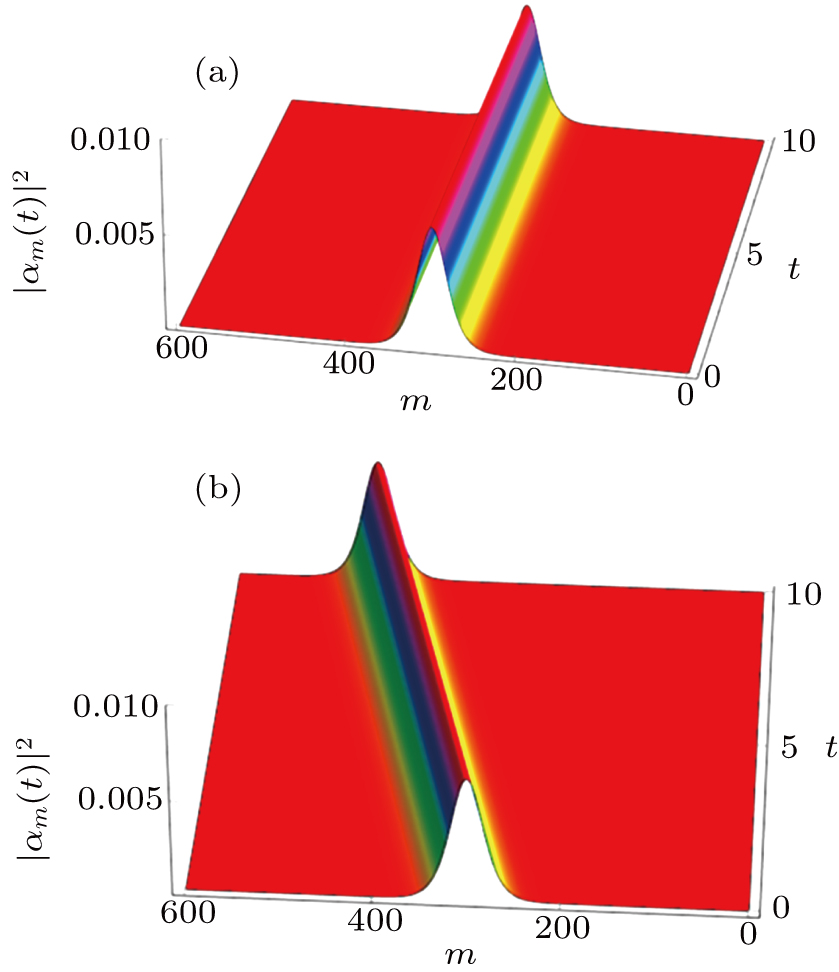
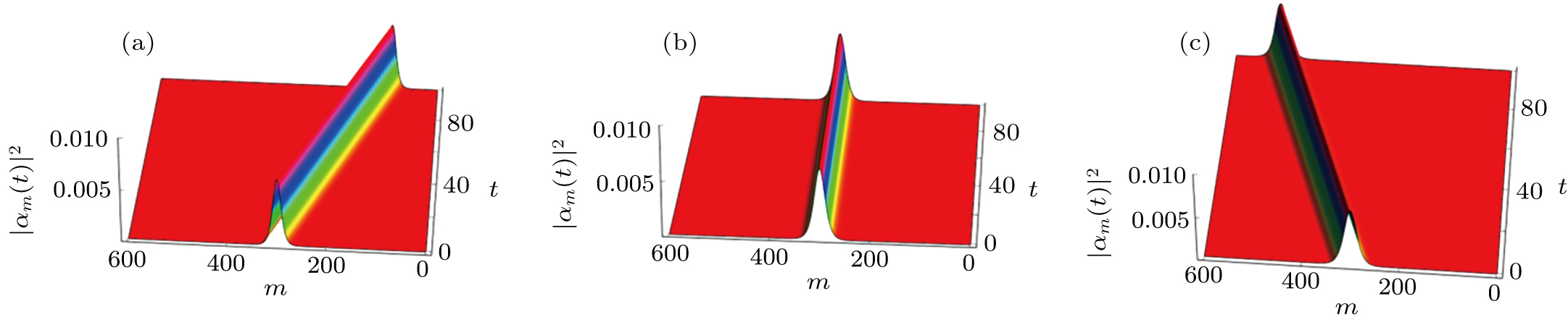
Fig. 5. Temporal evolution of the Brillouin zone center mode: (a) D = 0, (b) D = 2. The relevant parameters are set to J = 1, S = 10, a = 1, γ =0.2, A = 10, C0 =0.08, m0 =300, , and B = 1.

When the DM interaction is introduced, the Brillouin zone center mode becomes a moving bright soliton mode, which reads

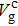
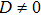
The velocity of the bright soliton mode (39) is equal to . In Fig. 5(b), we plot the time evolution of the Brillouin zone center mode (39). It is clearly seen that a moving bright soliton mode is presented in Fig. 5(b). From Eq. (37), we find that the soliton velocity is proportional to γ for the case of . Hence, in the easy-axis anisotropy weak ferromagnetic chain, varying γ can control the velocity of the Brillouin zone center mode.

4.4. Brillouin zone boundary mode

At the boundary of the first Brillouin zone 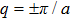, we have

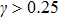
Obviously, the bright type localized spin wave mode may appear at the first Brillouin zone boundary for . When the DM interaction is absent, the Brillouin zone boundary mode is a stationary bright intrinsic localized mode, which has the following form:
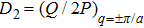
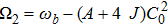
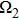
with and . Here, is the eigen-frequency for the Brillouin zone center mode, which lies within the linear spin wave frequency band. Hence, the Brillouin zone boundary mode (44) is a resonant mode[28,50] with the bright localized structure. Since such localized modes are in resonance with those linear spin waves, they have a limited lifetime in magnetic systems.

In the presence of the DM interaction, the Brillouin zone boundary mode is a bright soliton mode, which can be written as

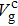
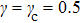
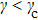
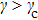
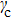
The velocity of the bright soliton mode (45) is equal to . From Eq. (42), we can confirm that the Brillouin zone center mode is still a stationary intrinsic localized mode with the bright profile when . What is more, we find that the velocities of the bright soliton modes are opposite for and . Hence, is the transition point of the velocity direction of the bright soliton mode. In Fig. 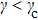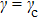6, we show the time evolution of the Brillouin zone boundary mode (45) for the three cases of , , and . 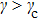Figure 6(b) displays a stationary bright type intrinsic localized resonant mode. In Figs. 6(a) and 6(c), we clearly see two moving bright soliton modes, whose speeds are along opposite directions. 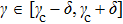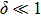Based on the above analysis, it not difficult to affirm that changing γ ( , ) can cause a reversal effect of the speed direction of the Brillouin zone boundary mode in the present easy-axis anisotropy weak ferromagnetic chain.

Fig. 6. Temporal evolution of the Brillouin zone boundary mode: (a) γ =0.4, (b) γ =0.5, (c) γ =0.6. The corresponding parameters are as follows: J = 1, S = 10, a = 1, D = 2, A = 10, C0 =0.08, m0 =300, , and B = 1.
5. Summary

We have studied the discrete modulational instability and bright type localized spin wave modes in a one-dimensional easy-axis weak ferromagnetic spin lattice system involving NNN couplings by using a semiclassical treatment. Carrying out a linear stability analysis, we calculated the growth rates of the modulational instability and we plotted the instability regions. Due to the induction of the DM interaction, the instability regions shift to the left end of the first Brillouin zone. Furthermore, we found that two asymmetric modulational instability regions appear in the left-hand and right-hand edges of the first Brillouin zone when γ is sufficiently large. By employing the results of the discrete modulational instability analysis, we can predict the parameter regions for the existence of bright nonlinear localized spin-wave modes.

We also obtained analytical forms of the bright nonlinear localized modes and analyzed their existence condition by means of a quasi-discreteness approach. The presence conditions of such bright localized modes were shown to be in agreement with the prediction of the modulational instability analysis. Our results show that the present weak ferromagnetic chain cannot support the stationary bright Brillouin zone center mode. What is more, the velocity of the Brillouin zone center mode is proportional to the value of γ. However, a stationary bright Brillouin zone center mode is possible in the system for the case of 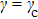. Surprisingly, we confirmed that controlling γ (around 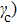can cause a reversal effect of the speed direction of the bright Brillouin zone boundary mode. This result is very interesting. Our finding may be helpful to understanding the effect of the long-range coupling on bright nonlinear localized modes in weak ferromagnets. Physically, the bright nonlinear localized mode is a localized wave packet, which can propagate without spreading and energy dissipation. Thus, the bright nonlinear localized mode in ferromagnets may have potential applications in quantum-information storage or transmission.[57] With the development of the experiment and theory,[58–70] we expect that our theoretical results will be confirmed in the related experiments.

Reference
[1] Baronio F Chen S Grelu P Wabnitz S Conforti M 2015 Phys. Rev. A 91 033804
[2] Wamba E Mohamadou A Ekogo T B Atangana J Kofane T C 2011 Phys. Lett. A 375 4288
[3] Stockhofe J Schmelcher P 2016 Physica D 328–329 9
[4] Kibler B Chabchoub A Gelash A Akhmediev N Zakharov V E 2015 Phys. Rev. X 5 041026
[5] Zhang J H Wang L Liu C 2017 Proc. R. Soc. A 473 20160681
[6] Cai L Y Wang X Wang L Li M Liu Y Shi Y Y 2017 Nonlin. Dynam. 90 2221
[7] Wang L Zhang L L Zhu Y J Qi F H Wang P Guo R Li M 2016 Commun. Nonlinear. Sci. Numer Simulat. 40 216
[8] Tabi C B Mohamadou A Kofane T C 2010 Eur. Phys. J. B 74 151
[9] Gori G Macrì T Trombettoni A 2013 Phys. Rev. E. 87 032905
[10] Xie Y D 2018 Acta Phys. Sin. 67 197502 (in Chinese) https://doi.org/10.7498/aps.67.197502
[11] Yang C Y Wazwaz A M Zhou Q Liu W J 2019 Laser Phys. 29 035401
[12] Liu W J Pang L H Shen Z W Lei M Teng H Wei Z Y 2016 Photon. Res. 4 111
[13] Liu W J Pang L H Han H N Tian W L Chen Hao Lei M Yan P G Wei Z Y 2015 Opt. Exp. 23 26023
[14] Su W H Xie J Y Wu T L Tang B 2018 Chin. Phys. B 27 097501
[15] Wang L Zhu Y J Wang Z Q Xu T Qi F H Xue Y S 2016 J. Phys. Soc. Jpn. 85 024001
[16] Baronio F Conforti M Degasperis A Lombardo S Onorato M Wabnitz S 2014 Phys. Rev. Lett. 113 034101
[17] Marklund M Shukla P K 2006 Phys. Rev. E 73 057601
[18] Meier J Stegeman G I Christodoulides D N Silberberg Y Morandotti R Yang H Salamo G Sorel M Aitchison J S 2004 Phys. Rev. Lett. 92 163902
[19] Carr L D Brand J 2004 Phys. Rev. Lett. 92 040401
[20] Kivshar Y S Peyrard M 1992 Phys. Rev. A 46 3198
[21] Kivshar Y S 1993 Phys. Lett. A 173 172
[22] Abdullaev F K Bouketir A Messikh A Umarov B A 2007 Physica D 232 54
[23] Daumont I Dauxois T Peyrard M 1997 Nonlinearity 10 617
[24] Yoshimura K 2004 Phys. Rev. E 70 016611
[25] Dauxois T Khomeriki R Ruffo S 2007 Eur. Phys. J. Spec. Top. 147 3
[26] Lai R Sievers A J 1999 Phys. Rep. 314 147
[27] Lai R Sievers A J 1998 Phys. Rev. B 57 3433
[28] Lai R Kiselev S A Sievers A J 1997 Phys. Rev. B. 56 5345
[29] Huang G Zhang S Hu B 1998 Phys. Rev. B 58 9194
[30] Nguenang J P Peyrard M Kenfack A J Kofané T C 2005 J. Phys.: Condens. Matter 17 3083
[31] Lakshmanan M Subash B Saxena A 2014 Phys. Lett. A 378 1119
[32] Kavitha L Mohamadou A Parasuraman E Gopi D Akila N Prabhu A 2016 J. Magn. Magn. Mater. 404 91
[33] Tang B Li G L Fu M 2017 J. Magn. Magn. Mater. 426 429
[34] Kavitha L Parasuraman E Gopi D Prabhu A Vicencio R A 2016 J. Magn. Magn. Mater. 401 394
[35] Dzyaloshinsky I 1958 J. Phys. Chem. Solids 4 241
[36] Moriya T 1960 Phys. Rev. Lett. 4 228
[37] Tang B Li D J Tang Y 2014 Chaos 24 023113
[38] Di K Zhang V L Lim H S Ng S C Kuok M H Yu J Yoon J Qiu X Yang H 2015 Phys. Rev. Lett. 114 047201
[39] Moon J H Seo S M Lee K J Kim K W Ryu J Lee H W McMichael R D Stiles M D 2013 Phys. Rev. B 88 184404
[40] Djoufack Z I Kenfack Jiotsa A Nguenang J P 2012 Eur. Phys. J. B 85 96
[41] Brächer T Boulle O Gaudin G Pirro P 2017 Phys. Rev. B 95 064429
[42] Je S G Kim D H Yoo S C Min B C Lee K J Choe S B 2013 Phys. Rev. B 88 214401
[43] Ding J Wu T Chang X Tang B 2018 Commun. Nonlinear. Sci. Numer. Simulat. 59 349
[44] Tang B Deng K 2017 Nonlin. Dynam. 88 2417
[45] Dyson F J 1956 Phys. Rev. 102 1217
[46] Dyson F J 1956 Phys. Rev. 102 1230
[47] Glauber R J 1963 Phys. Rev. 131 2766
[48] Smith H 1991 Introduction to Quantum Mechanics Singapore World Scientific
[49] Li P Wang L Kong L Q Wang X Xie Z Y 2018 Appl. Math. Lett. 85 110
[50] Huang G Shi Z P Xu Z 1993 Phys. Rev. B 47 14561
[51] Ablowitz M Segur H 1985 Solitons and the Inverse Scattering Transform Philadelphia SIAM
[52] Liu W Yu W Yang C Liu M Zhang Y Ming L 2017 Nonlin. Dynam. 89 2933
[53] Liu W Yang C Liu M Yu W Zhang Y Lei M 2017 Phys. Rev. E 96 042201
[54] Lü X Lin F 2016 Commun. Nonlinear Sci. Numer. Simulat. 32 241
[55] Li Z D Li Q Y Li L Liu W M 2007 Phys. Rev. E 76 026605
[56] Huang G Xu Z Xu W 1993 J. Phys. Soc. Jpn. 62 3231
[57] Li D C Li X M Li H Tao R Yang M Cao Z L 2015 Chin. Phys. Lett. 32 50302
[58] Liao H J Xie H D Liu Z Y Xie Z Y Li W Normand B Xiang T 2016 Chin. Phys. Lett. 33 77503
[59] Liu W J Liu M L Liu B Quhe R G Lei M Fang S B Teng H Wei Z Y 2019 Opt. Exp. 27 6689
[60] Dai J Wang P S Sun S S Pang F Zhang J S Dong X L Yue G Jin K Cong J Z Sun Y 2015 Chin. Phys. Lett. 32 127503
[61] Faizi E Eftekhari H 2015 Chin. Phys. Lett. 32 100303
[62] Fang J Han D M Liu H Liu H D Zheng T Y 2017 Acta Phys. Sin. 66 160302 (in Chinese) https://doi.org/10.7498/aps.66.160302
[63] Wang C J Chen A H Gao X L 2012 Acta Phys. Sin. 61 127501 (in Chinese) https://doi.org/10.7498/aps.61.127501
[64] Liu M L Ouyang Y Y Hou H R Liu W J Hou H R 2019 Chin. Opt. Lett. 17 020006
[65] Bai Y H Zhou W P Yun G H Bai N 2011 Acta Phys. Sin. 60 056805 (in Chinese) http://wulixb.iphy.ac.cn/CN/Y2011/V60/I5/056805
[66] Liu L Sandvik A W Guo W A 2018 Chin. Phys. B 27 087501
[67] Zhu S B Qian J Wang Y Z 2017 Chin. Phys. B 26 046702
[68] Yang D N Huang Y L Ni S L Zhou H X Mao Y Y Hu W Yuang J Jin K Zhang G M Dong X L 2016 Chin. Phys. B 25 077404
[69] Li D C Wang X P Li H Li X M Yang M Cao Z L 2016 Chin. Phys. Lett. 33 50301
[70] Li Y F Shen Y Y Kong X M 2012 Acta Phys. Sin. 61 107501 (in Chinese) https://doi.org/10.7498/aps.61.107501