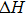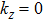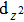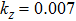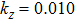† Corresponding author. E-mail:
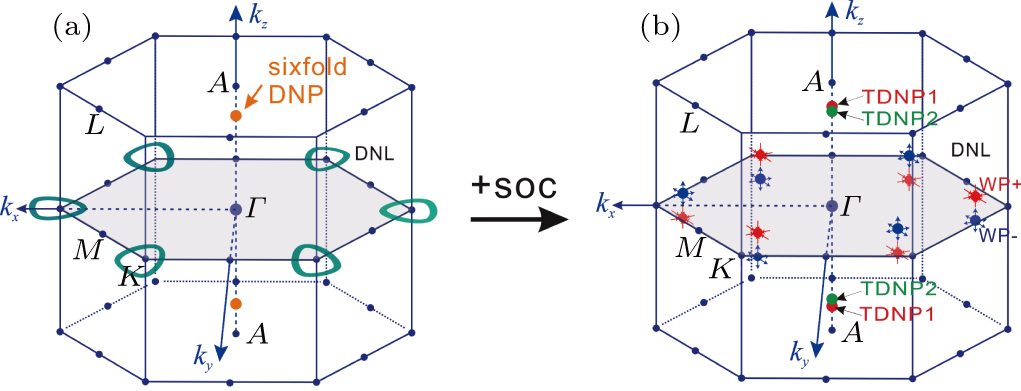
Recently, the non-centrosymmetric WC-type materials (i.e., MoP, ZrTe, TaN, etc) have attracted extensive interest due to the discovery of their topological properties. By means of the first-principles calculations, here we have investigated the structural, thermodynamic, elastic, and electronic properties of the WC-type MX compounds (TiS, TiSe, TiTe, ZrS, ZrSe, ZrTe, HfS, HfSe, and HfTe). Among these nine compounds, five of them (TiS, ZrS, ZrSe0.9, ZrTe, and Hf0.92Se) have been experimentally synthesized to crystallize in the WC-type structure and other four members have never been reported. Our calculations demonstrated that they are all structurally, thermodynamically, and dynamically stable, indicating that all of them should be possibly synthesized. We have also derived their elastic constants of single crystalline and their bulk and shear moduli in terms of the R. Hill approximations. Furthermore, in similarity to ZrTe, all these compounds have been theoretically derived to be topological semimetals. Whereas TiS is unique because of the coexistence of the Dirac nodal lines (DNLs) and sixfold degenerate nodal points (sixfold DNPs), the other eight members are revealed to exhibit coexisted Weyl nodes (WPs) and triply degenerate nodal points (TDNPs). Their electronic and topological properties have been further discussed.
All types of topological materials—such as topological insulators[1–3] and topological semimetals[4–8]—have attracted the attention of researchers because their nontrivial topological phases and unique transport properties, which could establish a fertile ground for quantum computers and spintronic applications. The topological semimetals play a leading role to pinpoint numerous fermions phenomena in solid crystal systems. Moreover, due to its protection mechanism and diverse band crossing points in the electronic band structure near the Fermi level, the topological semimetals family can be classified into different groups, such as three-dimensional Dirac semimetals,[9–25] Weyl semimetals,[26–48] Dirac nodal lines semimetals,[49–67] and semimetals with triply degenerate nodal points (TDNPs).[68–79,81] Furthermore, in the field of high energy physics, their realizations are also essential in solid crystals to establish a productive ground to study fundamental particles.
The non-centrosymmetric WC-type hexagonal structural MX family (MX = TaN, ZrTe, WC, MoP, TaS, TiS, TiSe, TiTe, ZrS, ZrSe, HfS, HfSe, and HfTe ) compounds have raised extensive attention due to the incredible innovation of two coexisted phenomenon of fermions: (i) three-component fermions (TDNPs), and (ii) two-component Weyl fermions (WPs) in their bulk phases around the Fermi level.[70–75,78,79] The existence of triply degenerated nodal points (TDNPs) can differentiate the MX family from other renowned topological semimetal candidates. Meanwhile, the properties related with the electronic TDNPs and WPs have been already discussed in detail by using theoretical and experimental approaches in the literature.[68–79] Interestingly, we have recently found that several WC-type compounds commonly host the unique phononic triply degenerate nodal points (TDNPs) and phononic Weyl nodes (WPs)[79,80] in their phonon spectra.
Following these advances in topological electronic and phononic properties of these MX compounds, further interests have been motivated to see which of the other compounds are isoelectronic and isostructural WC-type systems. Therefore, we have further analyzed the MX compounds, which are the combination of group IVB elements (Ti, Zr, and Hf) and VIA elements (S, Se, and Te) of the periodic table. This family contains nine compounds, in which five compounds (TiS, ZrS, ZrSe0.9, ZrTe, and Hf0.92Se) have been experimentally reported by Harry and Steiger, Sodeck, Orlygsson, Schewe-Miller et al.[82–89] However, the remaining four compounds (TiSe, TiTe, HfS, and HfTe) have not been reported experimentally to date. Nowadays, because of the advances in experimental synthesis techniques—such as, chemical vapor deposition (CVD), physical vapor deposition (PVD), and molecular beam epitaxy (MBE)—it is possible to synthesize these materials. In this sense, here we have assumed that these four unknown compounds of TiSe, TiTe, HfS, and HfTe also crystallize in the same WC-type structure.
Within this context, through first-principles calculations, we have used the WC-type structure to explore systematically their structural stability, enthalpy of formation, elastic and electronic properties. The MX family has a simple WC-type structure (space group of 
In this work, all of the results of the density functional theory (DFT)[90,91] have been obtained by employing Vienna ab-initio simulation package (VASP) code[92–94] with the projector augmented wave (PAW) technique[95,96] through generalized gradient approximations (GGA) of the Perdew–Burke–Ernzerhof (PBE) exchange–correlation function.[97,98] The implemented PAW-PBE pseudo-potentials of all elements (i.e., Ti, Zr, Hf, S, Se, and Te) are chosen by valence electrons states (i.e., 3p4s3d, 4s4p5s4d, 5p6s5d, and s2p4) and proper cutoff energy is selected according to their ENMAX parameters of elements in each compound. The Γ-centered grid is applied for significantly fasten energy converges for hexagonal structures with a proper set of k-points (21×21×21), and a very precise criterion of forces (below 0.0001 eV/Å) is used for structural optimizations.
In the literature,[99] the Voigt proposed a scheme for the determination of average elastic moduli of a single crystal to be established by assuming uniform strain throughout a lattice orientation of the crystal, and its values indicate the upper range of the actual moduli. Furthermore, in 1929, Reuss proposed another scheme to obtain the average elastic moduli of a single crystal by the assumption of uniform stress, and the values of resultant moduli indicate the lower frontier of the actual moduli of the crystals.[100] Both of these schemes are based on the assumption of uniform strain and stress in the crystal respectively and show the upper and lower limits of the actual elastic moduli but not the actual values of the elastic moduli of the crystal phase. To obtain the actual values of the elastic moduli (B&G) for a crystal phase, the R. Hill approximations[101] are used, and the resultant elastic moduli are equal to the arithmetic average value of the elastic moduli of the Voigt and Reuss schemes.[102] In addition, these elastic moduli were also used to determine the Poisson’s ratio ν and Young’s modulus E of the crystal phase.[103]
The WC-type crystal structure of the MX family contains two atoms per unit cell, which is non-centrosymmetric without inversion center as shown in Fig.
We have optimized the lattice structures of nine MX compounds with the WC-type structure. Table 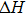
 |
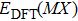
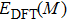

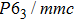
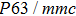
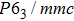

| Table 1.
DFT-derived lattice constants a and c and enthalpy of formation of single crystals, in comparison with available experimental data. . |
The elastic constants are crucial because they allow us to investigate the stability of a crystal phase. They are also associated with numerous basic solid-state phenomenons such as, phonon dispersion, thermal properties, inter-atomic potentials, mechanical properties, and hardness.[120,121] Most recently, the elastic properties of WC-type topological semimetals of MoP, ZrTe, and TaN have been theoretically investigated by Guo et al.[122–124] To elucidate the elastic properties of these MX compounds in this work, we have first repeated the calculations of the elastic properties of ZrTe which is isostructural to the MX family, and the accomplished results were comparable with the previous work.[123] Theoretically, our proposed nine compounds of the MX family have a hexagonal structure phase and they require four-order tensors of 3×3×3×3 order matrix of 81 elements.[125] Due to the hexagonal symmetry of the MX compounds, the number of elastic constants Cij is reduced from 81 to 5, which are C11, C12, C13, C33, and C44.[103,123] For these nine compounds, the derived elastic constants are compiled in Table 


| Table 2.
The DFT-derived elastic constants Cij in GPa, |
From Fig. 
Furthermore, we have derived the total densities of states (DOSs) and the partial DOSs of the MX compounds in Fig.
 | Fig. 3. The DFT-derived total densities of states and the partial density of states of MX (M = Ti, Zr, Hf; X = S, Se, Te). The Fermi level is set to the zero energy. |
We have derived the electronic band structures of these nine MX compounds in Figs. 
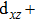
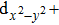

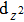


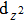
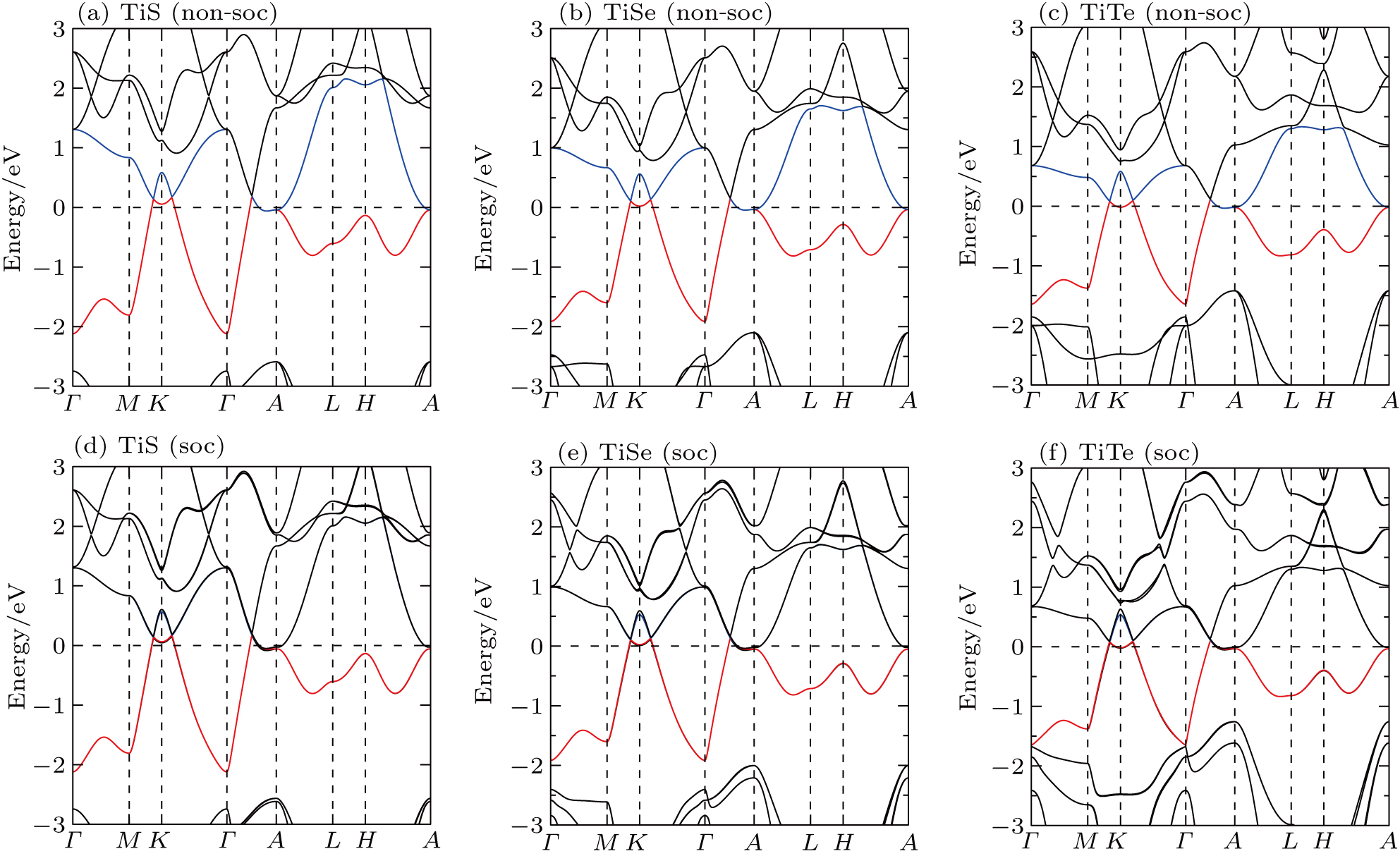 | Fig. 4. The DFT-derived electronic band structures of TiX (X = S, Se, Te): (a)–(c) without the SOC effect and (d)–(f) with the SOC effect. The Fermi level is set to the zero energy. |
 | Fig. 5. The DFT-derived electronic band structures of ZrX (X = S, Se, Te): (a)–(c) without the SOC effect and (d)–(f) with the SOC effect. The Fermi level is set to the zero energy. |
 | Fig. 6. The DFT-derived electronic band structures of HfX (X = S, Se, Te): (a)–(c) without the SOC effect and (d)–(f) with the SOC effect. The Fermi level is set to the zero energy. |
Because the masses of these elemental solids M and X are not very light, their SOC interactions should be considered. Once the SOC has been contained in their electronic band structures, we can see the highly apparent changes, particularly around the Fermi level. The only exception is the case TiS. Because TiS exhibits the weakest SOC effect among these nine compounds, as shown in Fig. 


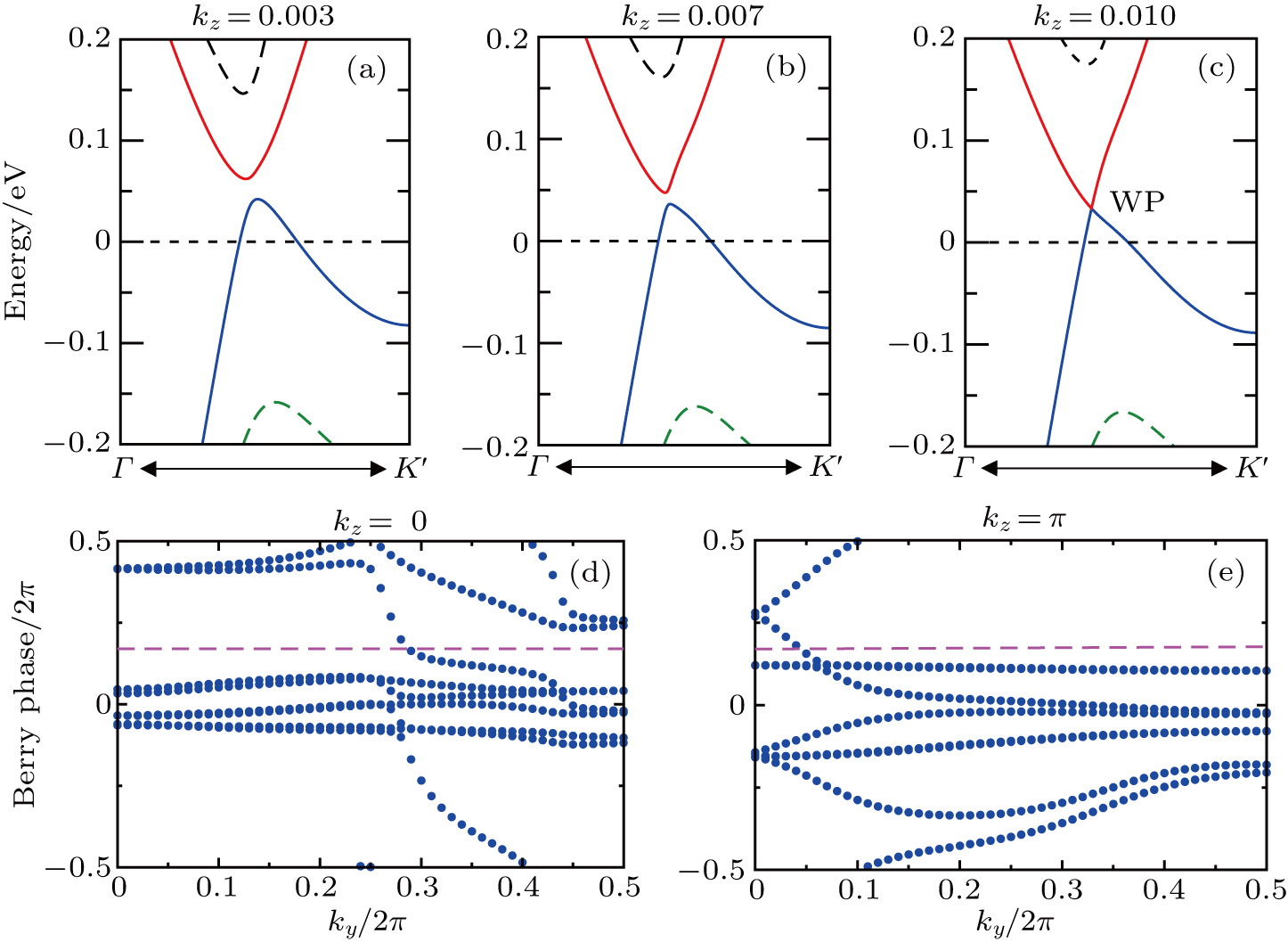
Furthermore, as for ZrTe in Ref. [71], we can illustrate the topological property of the electronic structure using the Wilson loop method. Here, we have selected HfSe as a prototypical example to show the non-trivial topological feature of its electronic structure. We have first plot the DFT-derived electronic structure around one of the WPs for HfSe in Figs. 
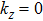
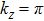
By employing the first-principles calculations, we have studied the structural, thermodynamic, elastic, and electronic properties of nine WC-type MX compounds (TiS, TiSe, TiTe, ZrS, ZrSe, ZrTe, HfS, HfSe, and HfTe). Five of them (TiS, ZrS, ZrSe0.9, ZrTe, and Hf0.92Se) have been theoretically derived to have comparable results with known experimental reported data. We have also predicted four new compounds of TiSe, TiTe, HfS, and HfTe which are thermodynamically and dynamically stable. All these compounds satisfy the mechanical criteria of hexagonal crystal phase, their bulk and shear moduli are obtained by R. Hill approximation. In addition, all these compounds have been theoretically proposed to be topological semimetals and revealed the analogous electronic band structures with the coexisted Weyl nodes and triply degenerate nodal points in their bulk phases like ZrTe compound, excluding TiS, due to the weak SOC effect.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] | |
| [100] | |
| [101] | |
| [102] | |
| [103] | |
| [104] | |
| [105] | |
| [106] | |
| [107] | |
| [108] | |
| [109] | |
| [110] | |
| [111] | |
| [112] | |
| [113] | |
| [114] | |
| [115] | |
| [116] | |
| [117] | |
| [118] | |
| [119] | |
| [120] | |
| [121] | |
| [122] | |
| [123] | |
| [124] | |
| [125] | |
| [126] | |
| [127] | |
| [128] |