† Corresponding author. E-mail:
Motivated by the growing interest in the novel quantum phases in materials with strong electron correlations and spin–orbit coupling, we study the interplay among the spin–orbit coupling, Kondo interaction, and magnetic frustration of a Kondo lattice model on a two-dimensional honeycomb lattice. We calculate the renormalized electronic structure and correlation functions at the saddle point based on a fermionic representation of the spin operators. We find a global phase diagram of the model at half-filling, which contains a variety of phases due to the competing interactions. In addition to a Kondo insulator, there is a topological insulator with valence bond solid correlations in the spin sector, and two antiferromagnetic phases. Due to the competition between the spin–orbit coupling and Kondo interaction, the direction of the magnetic moments in the antiferromagnetic phases can be either within or perpendicular to the lattice plane. The latter antiferromagnetic state is topologically nontrivial for moderate and strong spin–orbit couplings.
Exploring novel quantum phases and the associated phase transitions in systems with strong electron correlations is a major subject of contemporary condensed matter physics.[1–3] In this context, heavy fermion (HF) compounds play a crucial role.[3–7] In these materials, the coexisted itinerant electrons and local magnetic moments (from localized f electrons) interact via the antiferromagnetic exchange coupling, resulting in the famous Kondo effect.[8] Meanwhile, the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction, namely the exchange coupling among the local moments mediated by the itinerant electrons, competes with the Kondo effect.[9] This competition gives rise to a rich phase diagram with an antiferromagnetic (AFM) quantum critical point (QCP) and various emergent phases nearby.[3,10]
In the HF metals, experiments[11,12] have provided strong evidence for local quantum criticality,[13,14] which is characterized by the beyond-Landau physics of Kondo destruction at the AFM QCP. Across this local QCP, the Fermi surface jumps from large in the paramagnetic HF liquid phase to small in the AFM phase with Kondo destruction. A natural question arises: how does this local QCP connect to the conventional spin density wave (SDW) QCP described by the Hertz–Millis theory?[15,16] A proposed global phase diagram[17–20] makes this connection via the tuning of the quantum fluctuations in the local-moment magnetism. Besides the HF metals, it is also interesting to know whether a similar global phase diagram can be realized in Kondo insulators (KIs), where the chemical potential is inside the Kondo hybridization gap when the electron filling is commensurate. The KIs are band insulators where the band gap originates from nontrivial strong electron-correlation effects. A Kondo-destruction transition is expected to accompany the closure of the band gap. The question that remains open is: do the local moments immediately order or do they form a different type of magnetic state, such as spin liquid or valence bond solid (VBS), when the Kondo-destruction takes place?
Recent years have seen extensive studies about the effect of a fine spin–orbit coupling (SOC) on the electronic bands. In topological insulators (TIs), the bulk band gap opens due to a non-zero SOC, and there exist gapless surface states. The nontrivial topology of the band structure is protected by the time reversal symmetry (TRS). Even for a system with broken TRS, the conservation of combination of TRS and translational symmetry can give rise to a topological antiferromagnetic insulator (T-AFMI).[21] In general, these TIs and TAFIs can be tuned to topologically trivial insulators via topological quantum phase transitions. But how the strong electron correlations influence the properties of these symmetry dictated topological phases and the related phase transitions is still under active discussion.
The SOC also has important effects in HF materials.[20] For example, the SOC can produce a topologically nontrivial band structure and induce exotic Kondo physics.[22,23] It may give rise to a topological Kondo insulator (TKI),[24] which has been invoked to understand the resistivity plateau of the heavy-fermion SmB6 at low temperatures.[25]
From a more general perspective, the SOC provides an additional tuning parameter enriching the global phase diagram of the HF systems.[20,26] Whether and how the topological nontrivial quantum phases can emerge in this phase diagram is a timely issue. Recent studies have advanced a Weyl–Kondo semimetal phase.[27] The new heavy fermion compound Ce3Bi4Pd3 displays thermodynamic[28] and zero-field Hall transport[29] properties that provide evidence for the salient features of the Weyl–Kondo semimetal. These measurements probe the linearly dispersing electronic excitations with a velocity that is renormalized by several orders of magnitude and singularities in the Berry-curvature distribution.
Theoretical studies are also of interest for a Kondo lattice model defined on a honeycomb lattice,[30] which readily accommodates the SOC.[31] In the diluted carrier limit, this model supports a nontrivial Dirac–Kondo semimetal (DKSM) phase, which can be tuned to a TKI by increasing the SOC.[32] In Ref. [30], it was shown that, at half-filling, increasing the Kondo coupling induces a direct transition from a TI to a KI. A related model, with the conduction-electron part of the Hamiltonian described by a Haldane model[33] on the honeycomb lattice, was subsequently studied.[34]
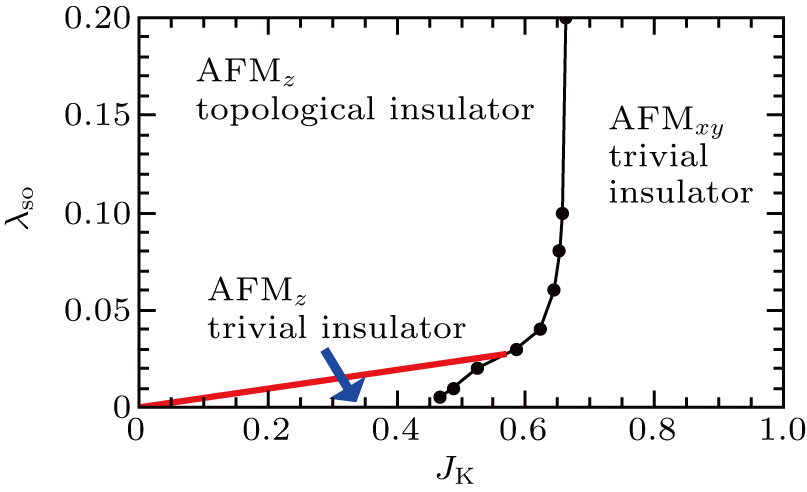
Here we investigate the global phase diagram of a spin–orbit-coupled Kondo lattice model on the honeycomb lattice at half-filling. We show that the competing interactions in this model give rise to a very rich phase diagram containing a TI, a KI, and two AFM phases. We focus on discussing the influence of magnetic frustration on the phase diagram. In the TI, the local moments develop a VBS order. In the two AFM phases, the moments are ordered, respectively, in the plane of the honeycomb lattice (denoted as AFMxy) and perpendicular to the plane (AFMz). Particularly in the AFMz phase, the conduction electrons may have a topologically nontrivial band structure, although the TRS is explicitly broken. This T-AFMz state connects to the trivial AFMz phase via a topological phase transition as the SOC is reduced.
The remainder of the paper is organized as follows. We start by introducing the model and our theoretical procedure in Section
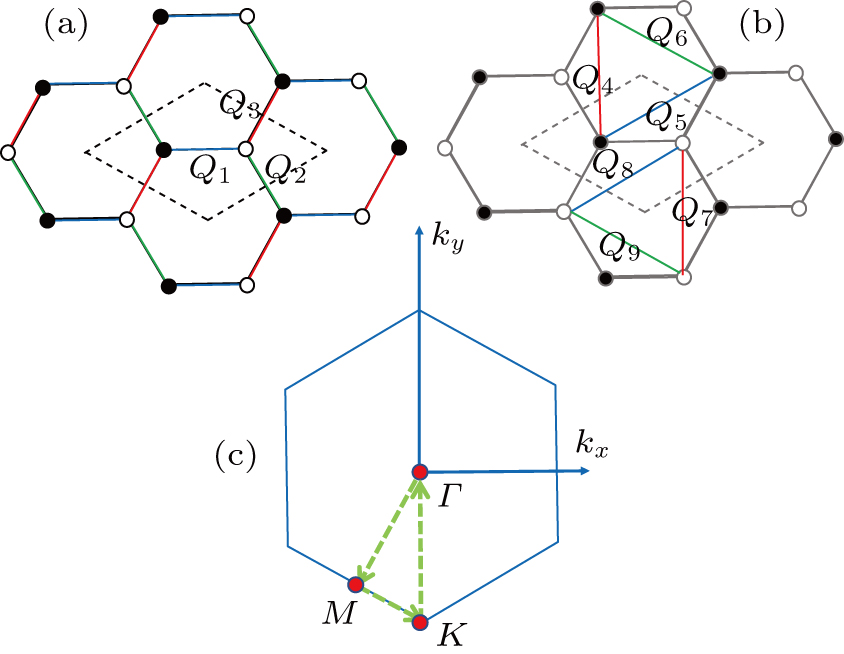
The model that we consider here is defined on an effective double-layer honeycomb lattice. The top layer contains conduction electrons realizing the Kane–Mele Hamiltonian.[31] The conduction electrons are Kondo coupled (i.e., via AF exchange coupling JK) to the localized magnetic moments in the bottom layer. The local moments interact among themselves through direct exchange interaction, as well as the conduction electron mediated RKKY interaction; the interactions are described by a simple J1–J2 model. Both the conduction bands and the localized bands are half-filled. This Kondo-lattice Hamiltonian takes the following form on the honeycomb lattice:
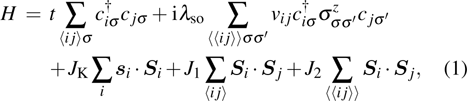 |
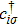
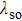
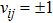
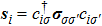

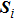
We use the spinon representation for 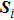
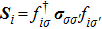
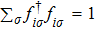
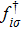
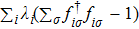
 |



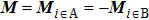
To take into account the Kondo hybridization and the possible magnetic order on an equal footing, we follow the treatment of the Heisenberg interaction as outlined in Eq. (
 |
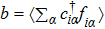
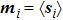
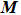
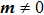
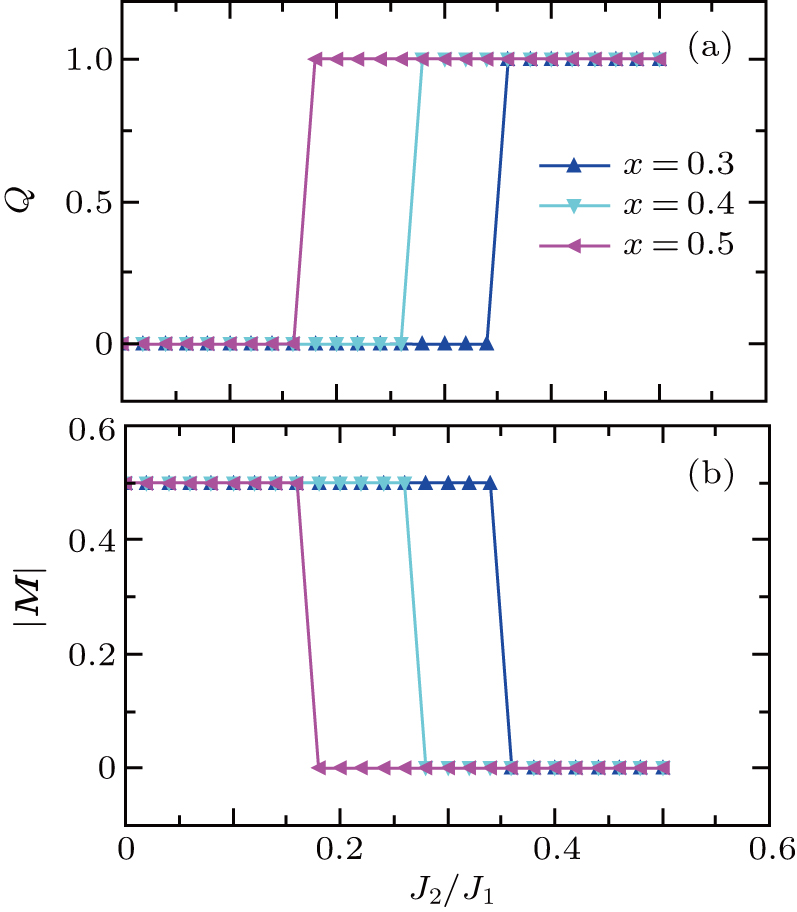
Because of the complexity of the full Hamiltonian, we start by setting JK = 0 and discuss the possible ground-state phases of the J1–J2 Heisenberg model for the local moments. By treating the problem at the saddle-point level in Eq. (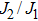
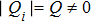
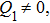
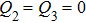

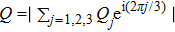
 | Fig. 2. Ground-state phase diagram of the J1–J2 Hamiltonian for the local moments in the x–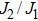
|
In Fig. 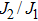
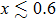
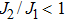
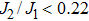
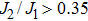
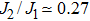
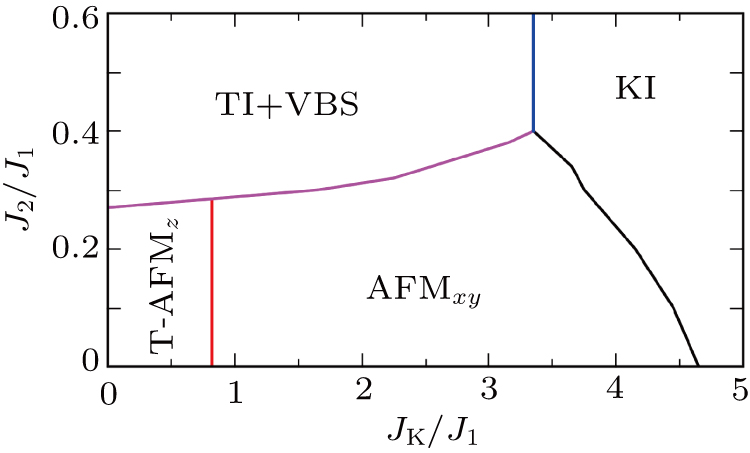
We now turn to the global phase diagram of the full model by turning on the Kondo coupling. For definiteness, we set J1 = 1 and consider t = 1 and 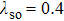

In our calculation, the phase boundaries are determined by sweeping JK while along multiple horizontal cuts for several fixed J2/J1 values, as shown in Fig. 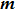
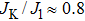
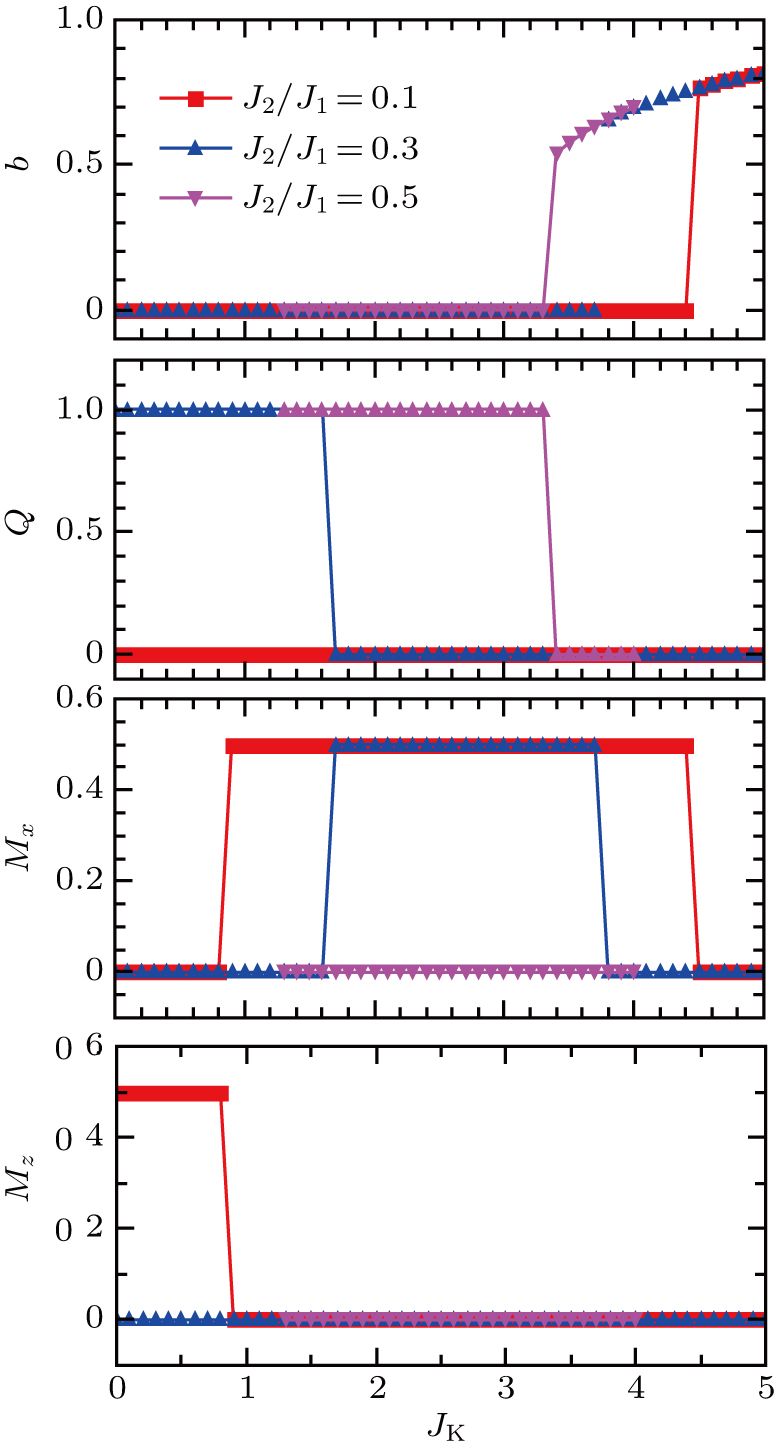 | Fig. 5. Evolution of parameters (a) b, (b) Q, (c) Mx, and (d) Mz as a function of JK for different ratios of J2/J1. |
For sufficiently large JK, the Kondo hybridization b is nonzero (see Fig. 
Several remarks are in order. The phase diagram, Fig.
In this section, we discuss the properties of the AFMxy and AFMz states, in particular to address their topological nature. For a clear discussion, we fix t = 1, J1 = 1, and J2 = 0. Since the Kondo hybridization is not essential to the nature of the AFM states, in this section we simply the discussion by setting y = 0.
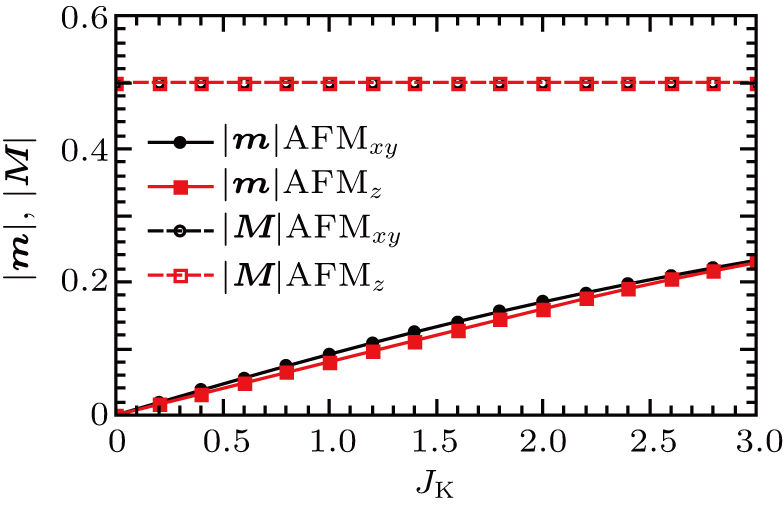
We start by defining the order parameters of the two states
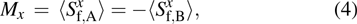 |
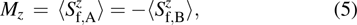 |
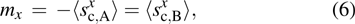 |
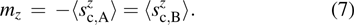 |

We then discuss the energy competition between the AFMxy and AFMz states. The conduction electron part of the mean-field Hamiltonian reads
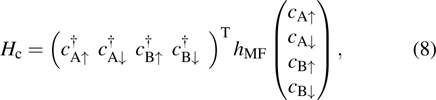 |
 |
 |
 |

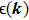
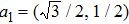
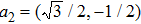
 |
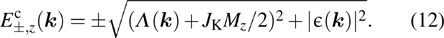 |
The eigenenergies of the spinon band can be obtained in a similar way
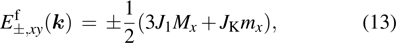 |
 |
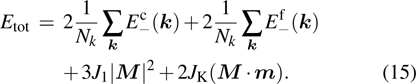 |


By comparing the expressions of 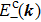
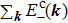
Meanwhile, from Eqs. (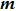
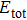
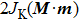

With increasing JK, the two effects from the magnetic orders compete, resulting in different magnetic ground states as shown in Fig. 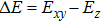
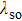
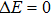
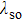
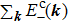
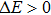
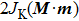
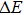
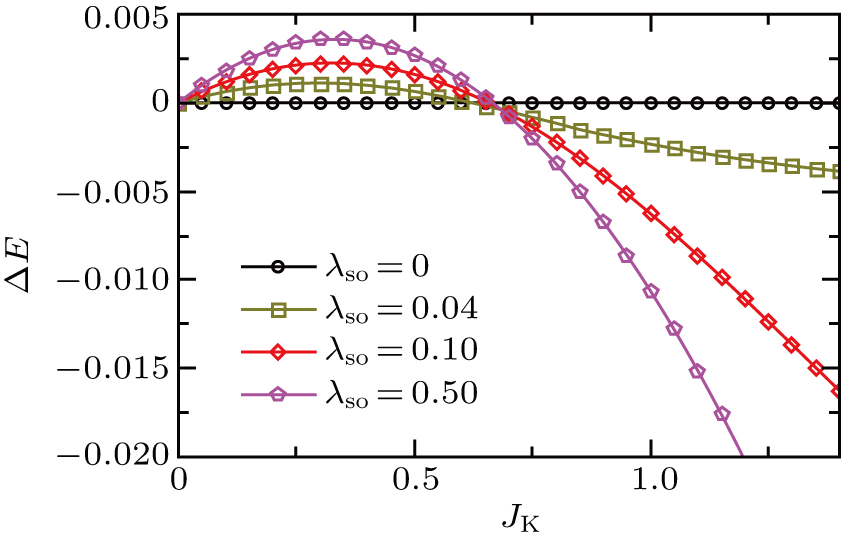 | Fig. 7. Energy difference between AFMz and AFMxy states as a function of JK for various values of spin–orbital coupling 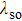
|
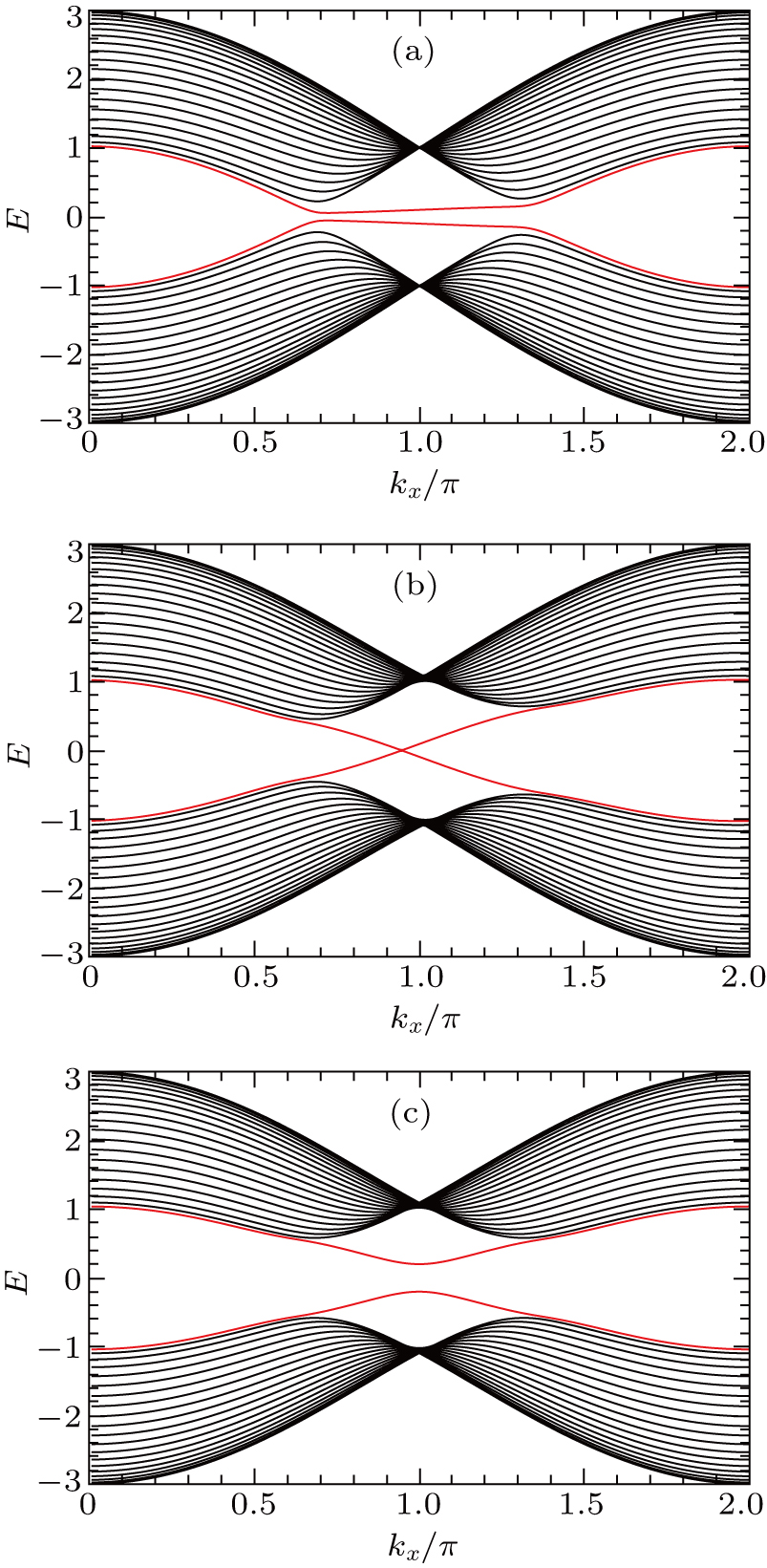
Next we discuss the topological nature of the AFMz and AFMxy states. In the absence of Kondo coupling JK, the conduction electrons form a TI, which is protected by the TRS. There, the left- and right-moving edge states connecting the conduction and valence bands are respectively coupled to up and down spin flavors (eigenstates of the Sz operator) as the consequence of SOC, and these two spin polarized edge states do not mix.
Once the TRS is broken by the AFM order, generically, topologically nontrivial edge states are no longer guaranteed. However, in the AFMz state, the structure of the Hamiltonian for the conduction electrons is the same as that in a TI. This is clearly shown in Eq. (

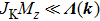
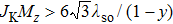
For the AFMxy state, we can examine the Hamiltonian for the conduction electrons in a similar way. As shown in Eq. (
To support this analysis, we perform calculations of the energy spectra of the conduction electrons in the AFMz and AFMxy states, as shown in Eqs. (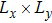
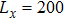
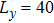
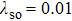
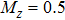

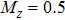
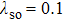
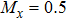

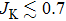
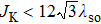
We have discussed the properties of various phases in the ground-state phase diagram of the spin–orbit-coupled Kondo lattice model on the honeycomb lattice at half filling. We have shown how the competition of SOC, Kondo interaction, and magnetic frustration stabilizes these phases. For example, in the AFM phase the moments can order either along the z-direction or within the x–y plane. In our model, the AFM order is driven by the RKKY interaction, and the competition of SOC and Kondo interaction dictates the direction of the ordered magnetic moments.
Throughout this work, we have discussed the phase diagram of the model at half filling. The phase diagram away from half-filling is also an interesting problem. We expect that the competition between the AFMz and AFMxy states persist at generic fillings, but the topological feature will not. Another interesting filling would be the dilute-carrier limit, where a DKSM exists, and can be tuned to a TKI by increasing the SOC.[32]
In this work, we have considered a particular type of SOC, which is inherent in the band structure of the itinerant electrons. In real materials, there are also SOC terms that involve the magnetic ions. Such couplings will lead to models beyond the current work, and may further enrich the global phase diagram.
Although the model in this work is defined on the honeycomb lattice, our conclusion on the global phase diagram is quite general, and will be important in understanding the nature of the transition between the Kondo insulating phase and the antiferromagnetic phase in real materials. For example, the Kondo insulator compound SmB6 undergoes a magnetic transition under pressure.[44] The Kondo-insulator-to-antiferromagnet transition may also be realized by doping CeNiSn with Pt or Pd ions since both CePtSn and CePdSn are antiferromagnetic at low temperatures.[44–46] Nontrivial topological properties in the antiferromagnetic phase are expected given that the 5d electrons of CePtSn may contain a large SOC. Moreover, because the Kane–Mele model describes the electron states in graphene, our model may also shed light on the properties of graphene with 5d adatoms.[47]
We have investigated the ground state phase diagram of a spin–orbit coupled Kondo lattice model at half-filling. The combination of SOC, Kondo and RKKY interactions produces various quantum phases, including a Kondo insulator, a topological insulator with VBS spin correlations, and two AFM phases. Depending on the strength of SOC, the magnetic moments in the AFM phase can be either ordered perpendicular to or in the x–y plane. We further show that the z-AFM state is topologically nontrivial for strong and moderate SOC, and can be tuned to a topologically trivial one via a topological phase transition by varying either the SOC or the Kondo coupling. Our results shed new light on the global phase diagram of heavy fermion materials.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] |