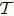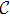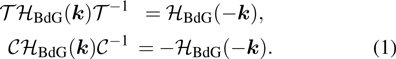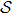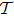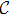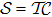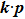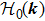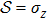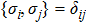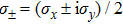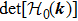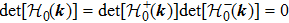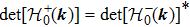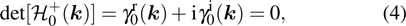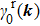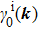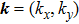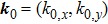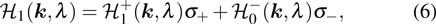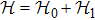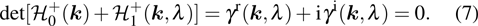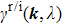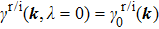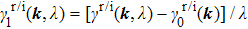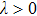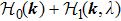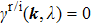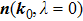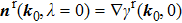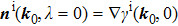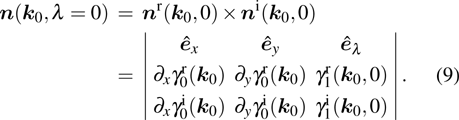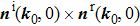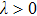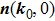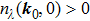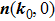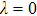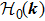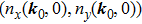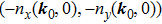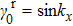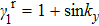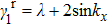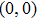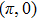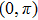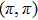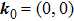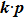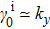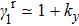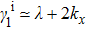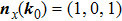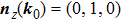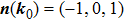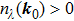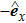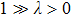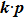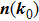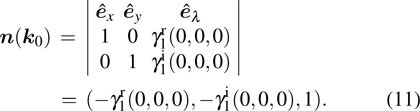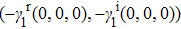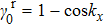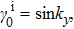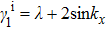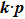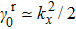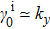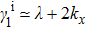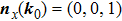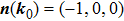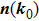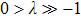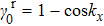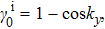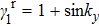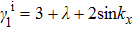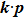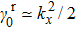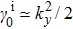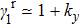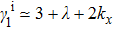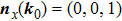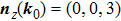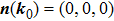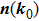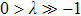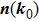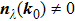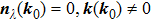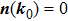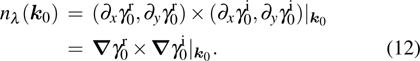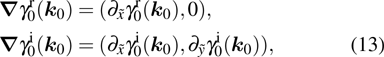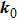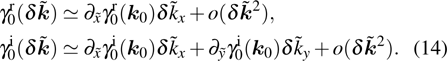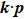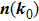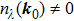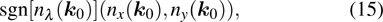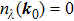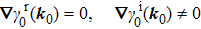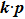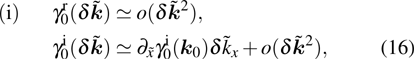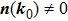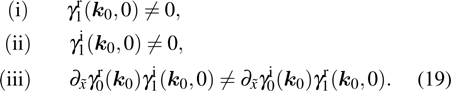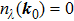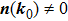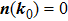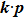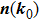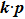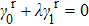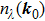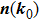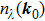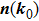Cite this Article
Fu Peiyuan, Yang Zhesen, Hu Jiangping. Local evolutions of nodal points in two-dimensional systems with chiral symmetry. Chinese Physics B, 2019, 28(7): 077101  
Permissions
Local evolutions of nodal points in two-dimensional systems with chiral symmetry
Fu Peiyuan1, 2, Yang Zhesen1, 2, †, Hu Jiangping1, 3, 4
Beijing National Laboratory for Condensed Matter Physics, and Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
Kavli Institute of Theoretical Sciences, University of Chinese Academy of Sciences, Beijing 100190, China
Collaborative Innovation Center of Quantum Matter, Beijing 100190, China

 

† Corresponding author. E-mail: yangzs@iphy.ac.cn

Abstract

Two-dimensional systems with chiral symmetry allow stable discrete band crossings (nodal points) in Brillouin zones. Here we study the local evolutions of these nodal points under chiral symmetry preserving perturbations. We find that these evolutions can be classified by different types of local models around the nodal points. Several concrete examples are calculated to illustrate our results.

PACS: 71.90.+q;03.65.Vf
Keyword:nodal points;chiral symmetry;k · p model
1. Introduction

Topology has emerged as a central concept in the research field of condensed matter physics for over 30 years.[1–3] By combining topology and band theory, we can calculate the Berry connection which can be viewed as a U(1) gauge field in the Brillouin zone (BZ) to obtain a topological quantity, the Chern number. Hence, all the two-dimensional insulators can be further classified by the Chern class, based on the first Chern number. Inspired by this new approach to classify the phase of matter beyond the Landau’s spontaneous symmetry breaking approach, many new states of gapped phases have been found both theoretically and experimentally, such as quantum spin Hall insulators, three-dimensional topological insulators, topological crystalline insulators, and topological superconductors.[4–8] These new phases all focus on gapped systems, whose Berry connection and Berry curvature can be well defined in the whole BZ.

Recently, the concepts of topology are found to be well defined in gapless systems, namely, topological protected semimetals (TS).[9] In these semimetals, there exist topologically stable band degeneracies in the BZ, which are robust against weak (symmetry preserving) perturbations. According to the dimension of band degeneracies, these topological protected semimetals can be classified roughly into the nodal point (NP) and nodal line semimetals. For the former case, the band degeneracies are discrete points in the BZ, such as Weyl semimetals, Dirac semimetals, and type-II Weyl semimetals.[10–12] For the latter case, the band degeneracies are one-dimensional nodal lines in the BZ, which can form loops, chains, links, or even knots.[13–19] Many topological semimetal phases have been predicted by first-principles calculations[20] and observed by angle-resolved photoemission spectroscopy (ARPES) experiments.[21] Searching for new topological phases and possible emergent behaviors has been new research frontiers both theoretically and experimentally.[22–38]

In general, the topologically stable band degeneracies are protected by discrete symmetries and global topological invariants, e.g., Chern number,[1] winding number,[39] or Z2 charge.[4,6] The topological stability of band degeneracies means that the NPs or nodal lines cannot be eliminated by symmetry preserving perturbations. In this paper, we consider a two-dimensional multi-band model with chiral symmetry, and study the NPs evolutions under possible small perturbations. The model can be interpreted as a Bogoliubov–de Gennes (BdG) Hamiltonian with time-reversal symmetry in addition to the electron band model. Under the time reversal 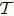and the particle–hole symmetry 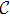, a BdG Hamiltonian transfers as[40]

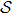
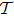
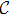
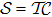
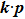
The chiral symmetry is the combination of and as . By calculating the moving directions of the NPs under generic forms of symmetry preserving perturbations, we classify the local evolutions of nodal points by the type of models around these points.

2. Hamiltonian and symmetry

Consider a general multi-band Bloch Hamiltonian 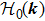with chiral symmetry 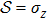. Under the chiral symmetry,

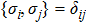
from the anti-commutation relations of Pauli matrices , we can easily check that the Hamiltonian can be written as
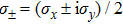
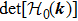
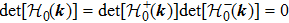
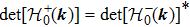
where . The condition for the band crossing is determined by the vanishing of , which can be expressed as . Since , the condition for gap closing is reduced to the following condition:
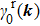
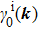
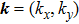
where and are the real and imaginary parts of , respectively. Generally, if we consider a two-dimensional (2d) system with , the solution of
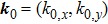
is discrete points (nodal points) in the BZ, as the co-dimension of the degeneracies is .[41] These NPs are stable against chiral symmetry preserving weak perturbations. Now assuming there exists a nodal point NP0 at in the BZ, we ask how will this NP moves under perturbations.

In general, a chiral symmetry preserving perturbation can be written as

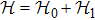
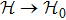
where (λ is the external parameter to control the perturbation, . When , . Under this perturbation, the gap closing condition is determined by
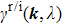
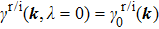
Obviously, satisfies . Hence we can re-express the equations for the gap closing under perturbations as
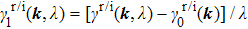
where . This expression simplifies the discussion in the next section.

3. Nodal points evolutions

Now we want to track the motion of the NP0 in the BZ as (λ changes. Without loss of generality, we can assume 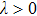in the following discussion. We consider a 2-band model for simplicity, which can be generalized to multi-band cases using the method we discuss below. The observation is that we can regard (λ as a third dimension in addition to the original 2d BZ. 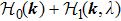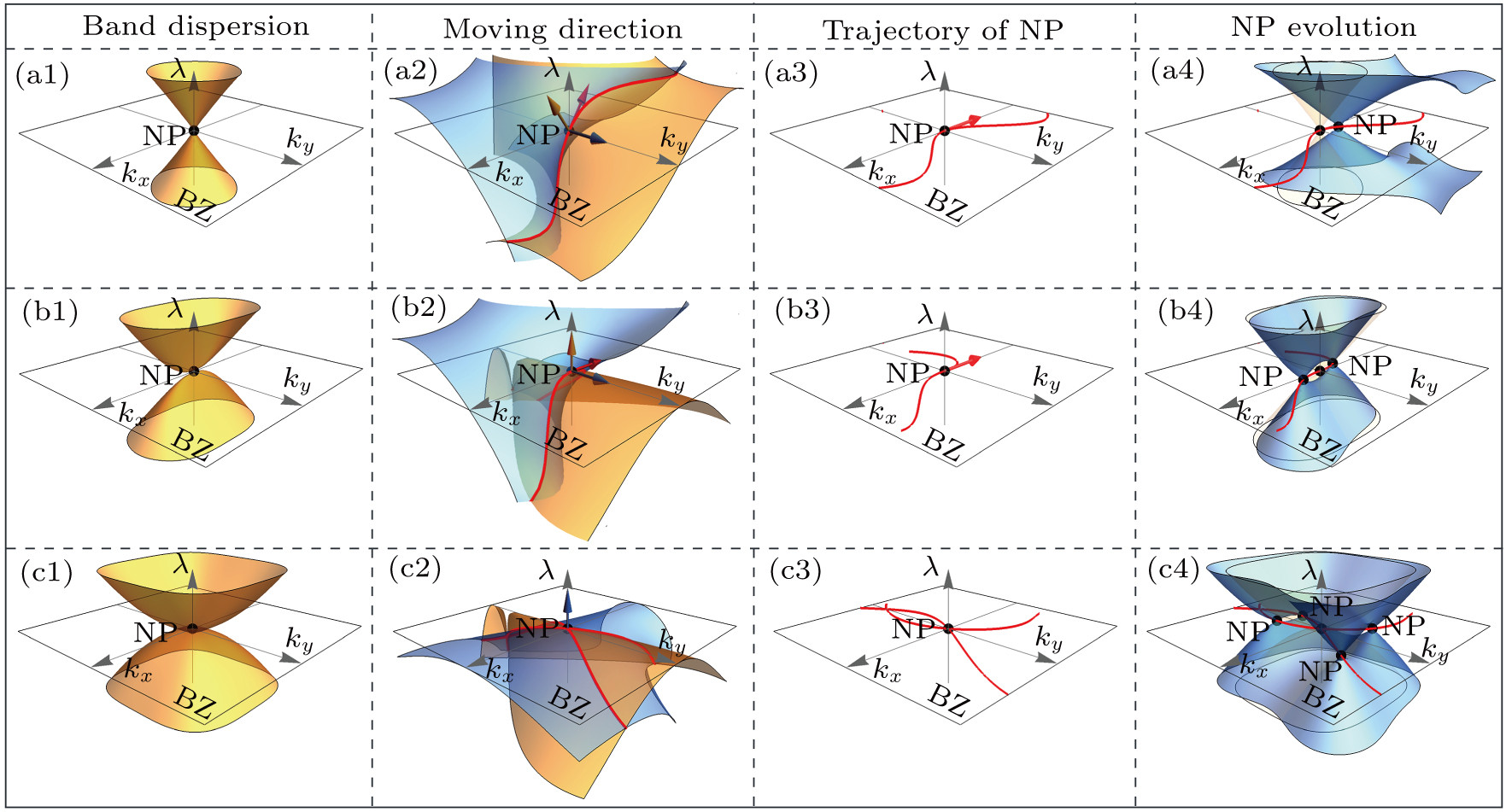Thus the band degeneracies of the Hamiltonian are 1d nodal lines which contain NP0, namely, , as shown in Fig. 1. The NP0 moves along the tangential direction of the nodal line under perturbations. Notice that the nodal line lies on both surfaces 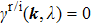, as shown in Fig. 1. So its tangent vector 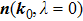is perpendicular to the gradient directions 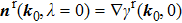and 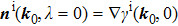of these two surfaces, respectively, as shown in Figs. 1(a) and 1(b). We write them down explicitly for further convenience

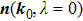
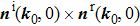
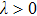
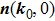
Notice that can also be defined as , which means we have two directions. However, only one of them is the moving direction with . We clarify that the moving direction is determined by the third component of , which is
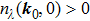
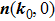
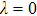
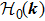
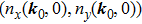
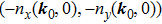
If , the moving direction of NP0 is the projection of in the plan (which is the 2d BZ of the original Hamiltonian ), , as shown in Fig. 1(d). If , the moving direction of the NP is . Next we use some concrete examples to illustrate the above procedures and provide some insight into the classification of the local evolutions.

Fig. 1. The method to determine the moving direction of a NP (black dot at the original point). Panels (a) and (b) show the surfaces , and their normal directions, respectively. Panel (c) shows that the tangential direction of the NL (with red color) is perpendicular to the above two normal directions. (d) The projection of the NL onto the λ = 0 plan is the trajectory of the NP and the tangential direction is the moving direction.
4. Examples

In the first example, we take 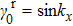, , , 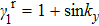and .

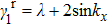The band degeneracies occur at 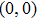, , 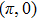, 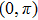and 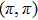in the 1st Brillouin zone. As they are locally separated, we can only consider the NP at 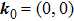for simplicity, which is shown in Fig. 2(a1). Around this point, the 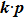model can be written as , , 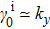, 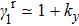and 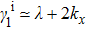. After a simple calculation, we obtain the two normal directions 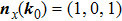and 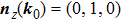. Based on these results, we can obtain the moving direction 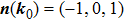, as shown in Fig. 2(a2). Because 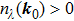, this NP moves along the 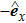direction under the perturbation with 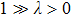, as shown in Fig. 2(a3). The NP moves along this direction, and cannot be eliminated by small external perturbations, as shown in Fig. 2(a4). This feature is only determined by the property of 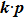Hamiltonian at the NP. 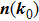Indeed, if we add a more general kind of perturbation , the moving direction is

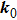
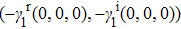
Thus the moving direction of the NP in the BZ is . We can easily check that the NP just moves in the BZ and cannot disappear or transit to multi-NPs unless under small finite perturbations.

Fig. 2. The classification of the evolutions of nodal points. The classification is based on the first column, that is and . The second and third columns show the constraints of the band dispersion around the NP and the possible geometry forms of the nodal line in kx–ky–λ space passing the NP, respectively. The last column shows the possible evolutions of NPs under a general form of perturbations. One can notice that the Dirac point (with linear dispersion along every direction) is stable against any chiral symmetric perturbation and cannot disappear nor transit to multi-NPs.

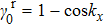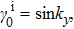
In the second example, we take , , and .

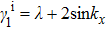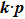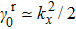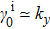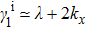In this case, we choose the NP at (0,0), the effective Hamiltonian around the NP is , , , and , as shown in Fig. 2(b1). Thus the two normal directions are 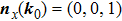and and the moving direction is 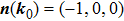, as shown in Fig. 2(b2). However, there is a crucial difference compared to example 1, that is, the third component of 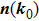is zero, which is and . Note that the NL is either above or blow the λ = 0 plan. We can check that external perturbations either eliminate the NP or transit it into two NPs. Figure 2(b4) shows the transition to two NPs with a finite perturbation 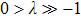. Notice that this feature is related to the band dispersion around the NP in which the dispersions are linear along one direction and quadratic along the other.

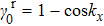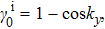
In the third example, we take , , 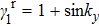and .

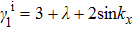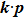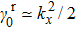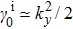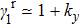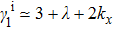In this case, the effective Hamiltonian around the NP (0,0) is , , , and , as shown in Fig. 2(c1). Thus the two normal directions are 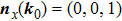and 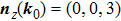and the moving direction is 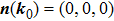, as shown in Fig. 2(c2). Notice that the calculated 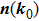is equal to zero, which means the nodal line does not have a well defined tangential direction at this point as shown in Fig. 2(c3). The external perturbations either eliminate the NP or transit it into multi-NPs. Figure 2(b4) shows the transition to four NPs with a finite perturbation 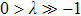. Notice that this feature is related to the band dispersion around the NP, which is non-linear along all directions.

These different features of the NP evolutions under perturbations reveal that NPs may have inner structures. We discuss these findings in detail in the following.

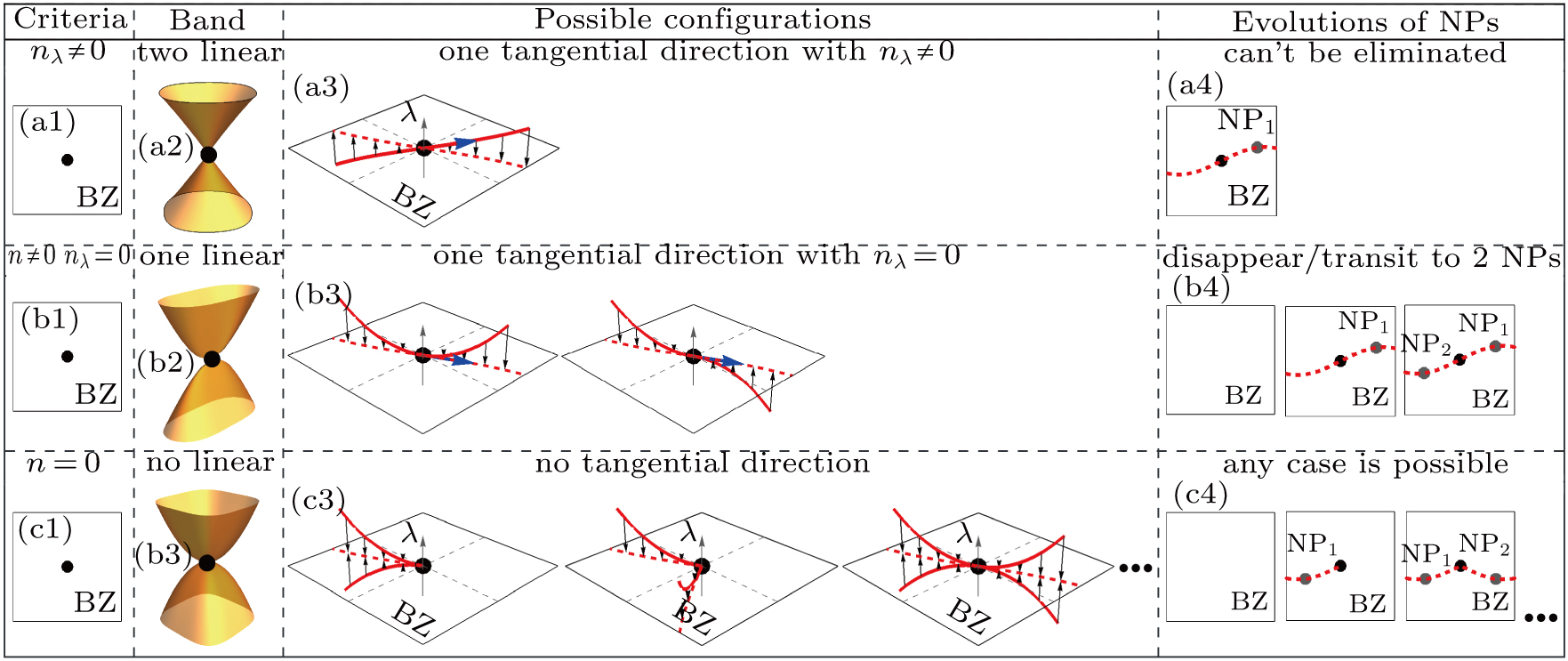
5. Classification of the evolutions

According to the above examples, we can classify the evolutions of the NPs by the third component of the moving direction 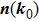into three cases

(I) ,

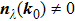(II) ,

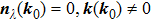(III) .

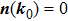We first notice that the above three classes are complete. Any 2d kind of NP must belong to one of them. The next step is to find the constraints of the above conditions to the band structure and possible evolutions of NPs. We analyze the three cases respectively.

Case (I) In this case, we first notice

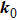
If this term does not equal to zero, one can always take a rotation of the momentum space around the NP , such that
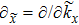
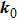
where and . Thus we can write down the effective Hamiltonian around the point, which is
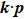
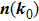
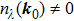
Thus the constraint guarantees that the Hamiltonian is linear along every direction around the NP to the leading order. Now we discuss the possible evolutions of NPs. As pointed out before, the evolution of NP depends on the tangential direction of the NL in the kx–ky–(λ space. Now if we consider the presence of the tangential direction with of the NL, the moving direction of the NP in the 2d BZ is
which means the topology of the NL around the NP must be equivalent to that in Fig. 3(a3). And the moving direction of the NP with small perturbations is unique. This kind of NP cannot be eliminated by external perturbations, as shown in Fig. 3(a4). The results are summarized in Fig. 3(a).

Fig. 3. The classification of the evolutions of nodal points. The classification is based on the first column, that is and . The second and third columns show the constraints of the band dispersion around the NP and the possible geometry forms of the nodal line in kx–ky–(λ space passing the NP, respectively. The last column shows the possible evolutions of NPs under a general form of perturbations. One can notice that the Dirac point (with linear dispersion along every direction) is stable against any chiral symmetric perturbation and cannot disappear nor transit to multi-NPs.

Case (II) The first condition 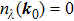implies the flowing three possible realizations:

(i) ,

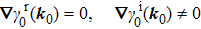(ii) ,

(iii) .

The effective 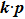Hamiltonian under these constrains can be written down as

These mean the dispersions at the NP are linear in one direction and quadratic or higher orders in the other to the leading order.

The second equation 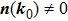requires the perturbation satisfying

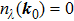
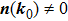
The conditions and require that the tangential direction of the NL at the NP is in the λ = 0 plan and the possible topology of the NL around the NP is shown in in Fig. 3(b3). Any external perturbation satisfying Eq. (19) transits it into two NPs or disappears. This case is summarized in Fig. 3(b).

Case (III) In this case, we first emphasize that we classify the general kind of perturbation terms. In case (II), if the perturbation terms break Eq. (19), the NP with linear and quadratic dispersions also satisfies 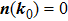. However, this requires a special kind of perturbation. Thus we do not consider this case in our classification tables. A more general case satisfying is

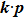
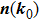
This means the Hamiltonian around the NP has quadratic or higher order dispersion to the leading order along both directions. The vanishing of implies that the NP is a singularity point on the NL. The results are summarized in Fig. 3(c).

6. Conclusion

We study the evolutions of NPs in systems with chiral symmetry, which can host discrete nodal points in the BZ. Figure 3 shows the classification of the NP evolutions under general form of perturbations. We exhaust all the possible evolution types of NPs and show that the classification can be achieved according to the type of 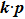model around the NPs. Only the nodal points with linear dispersion along every direction are robust against perturbations and cannot be gapped.

Reference
[1] Thouless D J Kohmoto M Nightingale M P den Nijs M 1982 Phys. Rev. Lett. 49 405 http://dx.doi.org/10.1103/PhysRevLett.49.405
[2] Haldane F D M 1988 Phys. Rev. Lett. 61 2015 http://dx.doi.org/10.1103/PhysRevLett.61.2015
[3] Kosterlitz J M Thouless D J 1973 J. Phys. C: Solid State Phys. 6 1181 http://dx.doi.org/10.1088/0022-3719/6/7/010
[4] Bernevig B A Hughes T A Zhang S C 2006 Science 314 1757 http://dx.doi.org/10.1126/science.1133734
[5] Bernevig B A Zhang S C 2006 Phys. Rev. Lett. 96 106802 http://dx.doi.org/10.1103/PhysRevLett.96.106802
[6] Fu L Kane C L Mele E J 2006 Phys. Rev. Lett. 98 106803 https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.98.106803
[7] Fu L Kane C L 2007 Phys. Rev. B 76 045302 http://dx.doi.org/10.1103/PhysRevB.76.045302
[8] Fu L 2011 Phys. Rev. Lett. 106 106802 http://dx.doi.org/10.1103/PhysRevLett.106.106802
[9] Burkov A A Hook M D Balents L 2011 Phys. Rev. B 84 235126 http://dx.doi.org/10.1103/PhysRevB.84.235126
[10] Wan X G Turner A M Vishwanath A Savrasov S Y 2011 Phys. Rev. B 83 205101 http://dx.doi.org/10.1103/PhysRevB.83.205101
[11] Soluyanov A A Gresch D Wang Z J Wu Q S Troyer M Dai X Bernevig B A 2015 Nature 527 495 http://dx.doi.org/10.1038/nature15768
[12] Young S M Zaheer S Teo J C Y Kane C L Mele E J Rappe A M 2012 Phys. Rev. Lett. 108 140405 http://dx.doi.org/10.1103/PhysRevLett.108.140405
[13] Bzdusek T Wu Q Ruegg A Sigrist M Soluyanov A 2016 Nature 538 75 http://dx.doi.org/10.1038/nature19099
[14] Bradlyn B Cano J Wang Z Vergniory M G Felser C Cava R J Bernevig B A 2016 Science 353 5037 http://dx.doi.org/10.1126/science.aaf5037
[15] Yan Z B Bi R Shen H T Lu L Zhang S C Wang Z 2017 Phys. Rev. B 96 041103 http://dx.doi.org/10.1103/PhysRevB.96.041103
[16] Yu R Fang Z Dai X Weng H M 2017 Front Phys. 12 127202 http://dx.doi.org/10.1007/s11467-016-0630-1
[17] Yu R Wu Q S Fang Z Weng H M 2017 Phys. Rev. Lett. 119 036401 http://dx.doi.org/10.1103/PhysRevLett.119.036401
[18] Xu Q N Yu R Fang Z Dai X Weng H M 2017 Phys. Rev. B 95 045136 http://dx.doi.org/10.1103/PhysRevB.95.045136
[19] Zhao J Z Yu R Weng H M Fang Z 2016 Phys. Rev. B 94 195104 http://dx.doi.org/10.1103/PhysRevB.94.195104
[20] Weng H M Dai X Fang Z 2016 J. Phys.: Condens. Matter 28 303001 https://doi.org/10.1088/0953-8984/28/30/303001
[21] Hasan M Z Xu S Y Bian G 2015 Phys. Scr. 2015 014001 https://doi.org/10.1088/0031-8949/2015/T164/014001
[22] Qin S.S. Hu L.H. Le C.C. Zeng J.F. Zhang F.C. Fang C. Hu J.P. 2019 arXiv:1901.04932
[23] Le C C Wu X X Qin S S Li Y X Thomale R Zhang F C Hu J P 2018 Pro. Natl. Acad. Sci. USA 115 8311 https://doi.org/10.1073/pnas.1803599115
[24] Le C C Qin S S Wu X X Dai X Fu P Y Hu J P 2017 Phys. Rev. B 96 115121 http://dx.doi.org/10.1103/PhysRevB.96.115121
[25] Xu X T Kang Z B Chang T R Lin H Bian G Yuan Z J Qu Z Zhang J L Jia S 2019 arXiv:1903.07901v1
[26] Ito S Arita M Haruyama J Feng B Chen W C Namatame H Taniguchi M Cheng C M Bian G Tang S J Chiang T C Sugino O Komori F Matsuda I 2019 arXiv:1903.07018v1
[27] Vail O Taylor P Folkes P Nichols B de Coster G 2019 arXiv:1903.06723v1
[28] Hamilton G A Park M J Gilbert M J 2019 arXiv:1903.00024v1
[29] Ma J C Deng K Zheng L Wu S F Liu Z Zhou S Y Sun D 2019 arXiv:1902.06874v1
[30] VanGennep D Paul T A Yerger C W Weir S T Vohra Y K Hamlin J J 2019 Phys. Rev. B 99 085204 http://dx.doi.org/10.1103/PhysRevB.99.085204
[31] Singh B Ghosh B Su C Lin H Agarwal A Bansil A 2018 Phys. Rev. Lett. 121 226401 http://dx.doi.org/10.1103/PhysRevLett.121.226401
[32] Xu B Zhao L X Marsik P Sheveleva E Lyzwa F Dai Y M Chen G F Qiu X G Bernhard C 2018 Phys. Rev. Lett. 121 187401 http://dx.doi.org/10.1103/PhysRevLett.121.187401
[33] Chen R Xu D H Zhou B 2018 Phys. Rev. B 98 235159 http://dx.doi.org/10.1103/PhysRevB.98.235159
[34] Benito-Matias E Molina R A 2019 Phys. Rev. B 99 075304 http://dx.doi.org/10.1103/PhysRevB.99.075304
[35] Ominato Y Tatsumi S Nomura K 2019 Phys. Rev. B 99 085205 http://dx.doi.org/10.1103/PhysRevB.99.085205
[36] Kim R Yang B J Kim C H 2019 Phys. Rev. B 99 045130 http://dx.doi.org/10.1103/PhysRevB.99.045130
[37] Hu Y J Aulestia E I P Tse K F Kuo C N Zhu J Y Lue C S Lai K T Goh S K 2018 Phys. Rev. B 98 035133 http://dx.doi.org/10.1103/PhysRevB.98.035133
[38] Habe T Koshino M 2018 Phys. Rev. B 98 125201 http://dx.doi.org/10.1103/PhysRevB.98.125201
[39] Dana I Avron Y Zak J 1985 J. Phys. C 18 L679 http://dx.doi.org/10.1088/0022-3719/18/22/004
[40] Chiu C K Teo J C Y Schnyder A P Ryu S 2016 Rev. Mod. Phys. 88 035005 http://dx.doi.org/10.1103/RevModPhys.88.035005
[41] Hořava P 2005 Phys. Rev. Lett. 95 016405 http://dx.doi.org/10.1103/PhysRevLett.95.016405