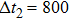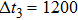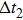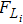† Corresponding author. E-mail:
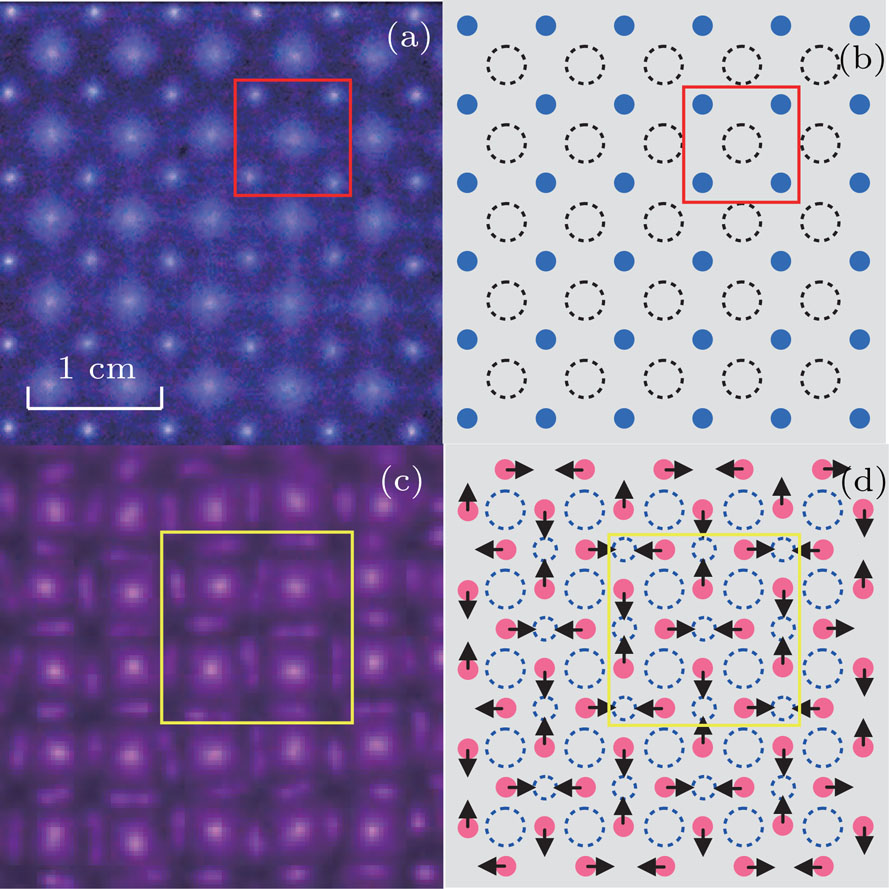
The influence of vibration on the spatiotemporal structure of the pattern in dielectric barrier discharge is studied for the first time. The spatiotemporal structure of the pattern investigated by an intensified charge-coupled device shows that it is an interleaving of three sublattices, whose discharge sequence is small rods–halos–large spots in each half-cycle of the applied voltage. The result of the photomultiplier indicates that the small rods are composed of moving filaments. The moving mode of the moving filaments is determined to be antisymmetric stretching vibration by analyzing a series of consecutive images taken by a high-speed video camera. The antisymmetric stretching vibration affects the distribution of wall charges and leads to the halos. Furthermore, large spots are discharged only at the centers of the squares consisting of vibrating filaments. The vibration mechanism of the vibrating filaments is dependent on the electric field of wall charges.
A pattern is a typical phenomenon of nonlinear self-organization, which can be generated in many systems, such as Faraday’s systems, convection systems, two-layer coupled reaction diffusion systems, gas discharge systems, and dielectric barrier discharge (DBD) systems.[1–9] DBD has recently attracted widespread attention because it has produced more types of patterns[10–17] due to its complex microscopic physical processes. In the DBD system, the spatiotemporal dynamics of the patterns depend on the electric field of wall charges deposited in discharge pulses. The observed patterns generally consist of several sublattices, with the next sublattices usually ignited at the center of each cell of the present sublattice.[18–20] For instance, Dong’s group obtained a square superlattice pattern, where the large spots were discharged at the centers of four small spots.[21] Dong et al. observed a hexagonal superlattice pattern containing only static filaments, in which the center spots were discharged at the center of the ambient spots.[22] Here, we observed an antisymmetric stretching vibration square superlattice pattern containing both static filaments and dynamic discharge vibrating filaments, in which the large spots are discharged only at the centers of the squares consisting of vibrating filaments, rather than at the centers of the antisymmetric stretching vibration.
During recent years, more and more dynamic patterns have been discovered and studied.[23,24] Generally, the pattern consists of several sets of sublattices, and the latter sublattices are discharged at the center of the last sub-lattice. For instance, Cui et al. observed a honeycomb pattern with moving filaments, and the central spots were discharged at the centers of the hexagons formed by the moving filaments.[25] Dong’s group obtained collective vibration filaments in a hexagonal superlattice pattern, in which the large spots were discharged at the center of the vibrating hexagonal small spots.[26] Prior to this, the effect of the vibrating filaments on the spatiotemporal dynamics of the pattern was the same as that of the static filaments. Here, we have studied the influence of vibration on the spatiotemporal structure of the pattern for the first time in the DBD system. Our observations provide a new idea for the formation mechanism of vibrating filaments, and promote the in-depth study of the formation mechanism of the pattern in the DBD system.
In this paper, the influence of vibration on the spatiotemporal structure of the pattern is studied for the first time in DBD. The spatiotemporal dynamics of the antisymmetric stretching vibration square superlattice pattern (ASVSSP) is studied using an intensified charge-coupled device (ICCD) camera and a photomultiplier. The vibration mode is analyzed based on the results of the high-speed video camera (HSVC). The vibration mechanism is studied by analyzing the interaction between the wall charges of the vibrating filaments. The study of the influence of vibration on the spatiotemporal structure provides a new way to understand the formation mechanism of the pattern.
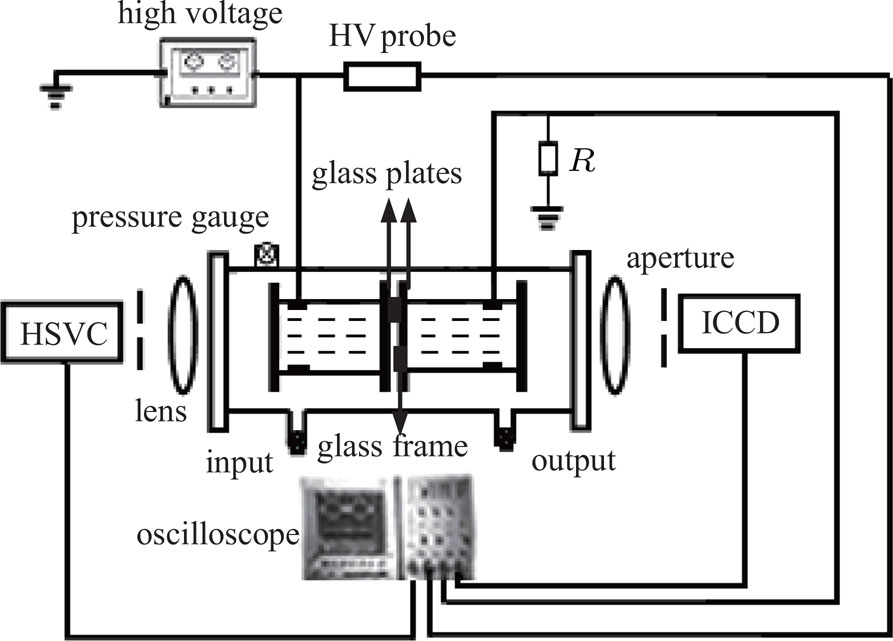
The schematic of the experimental setup is shown in Fig.
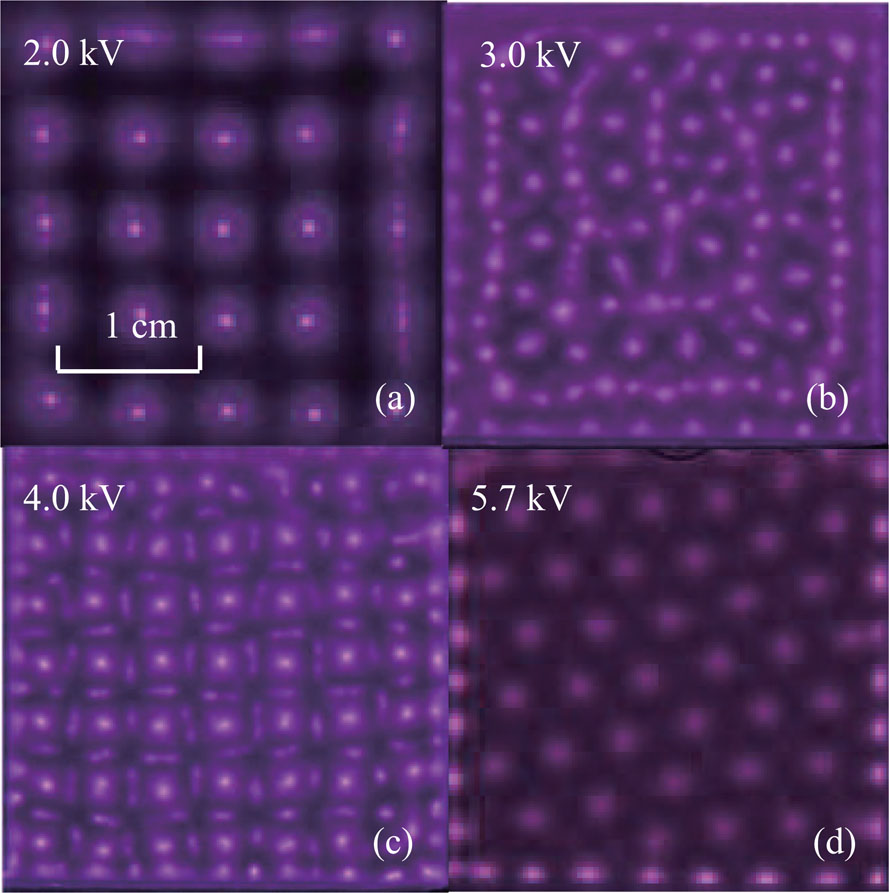
Figure
In order to investigate the spatiotemporal behavior of the ASVSSP, the time-resolved images are taken by the ICCD camera. Figure 
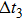
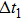
From Figs.
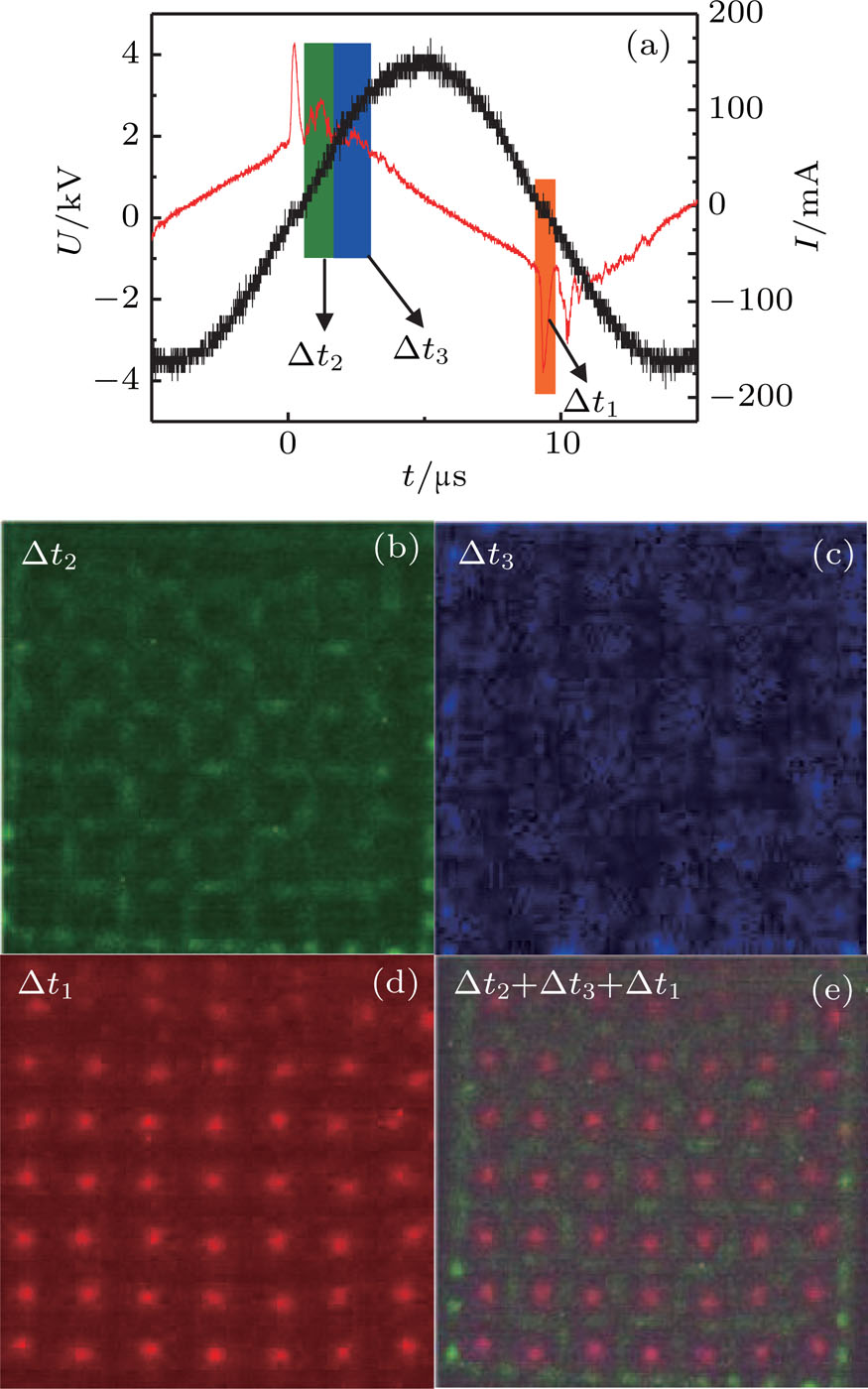
Figure
Here, to investigate the characteristic of the moving filaments, a series of consecutive frames of the ASVSSP are recorded by the HSVC with 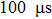
 | Fig. 5. A series of images of the ASVSSP recorded by the HSVC with 
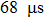
|
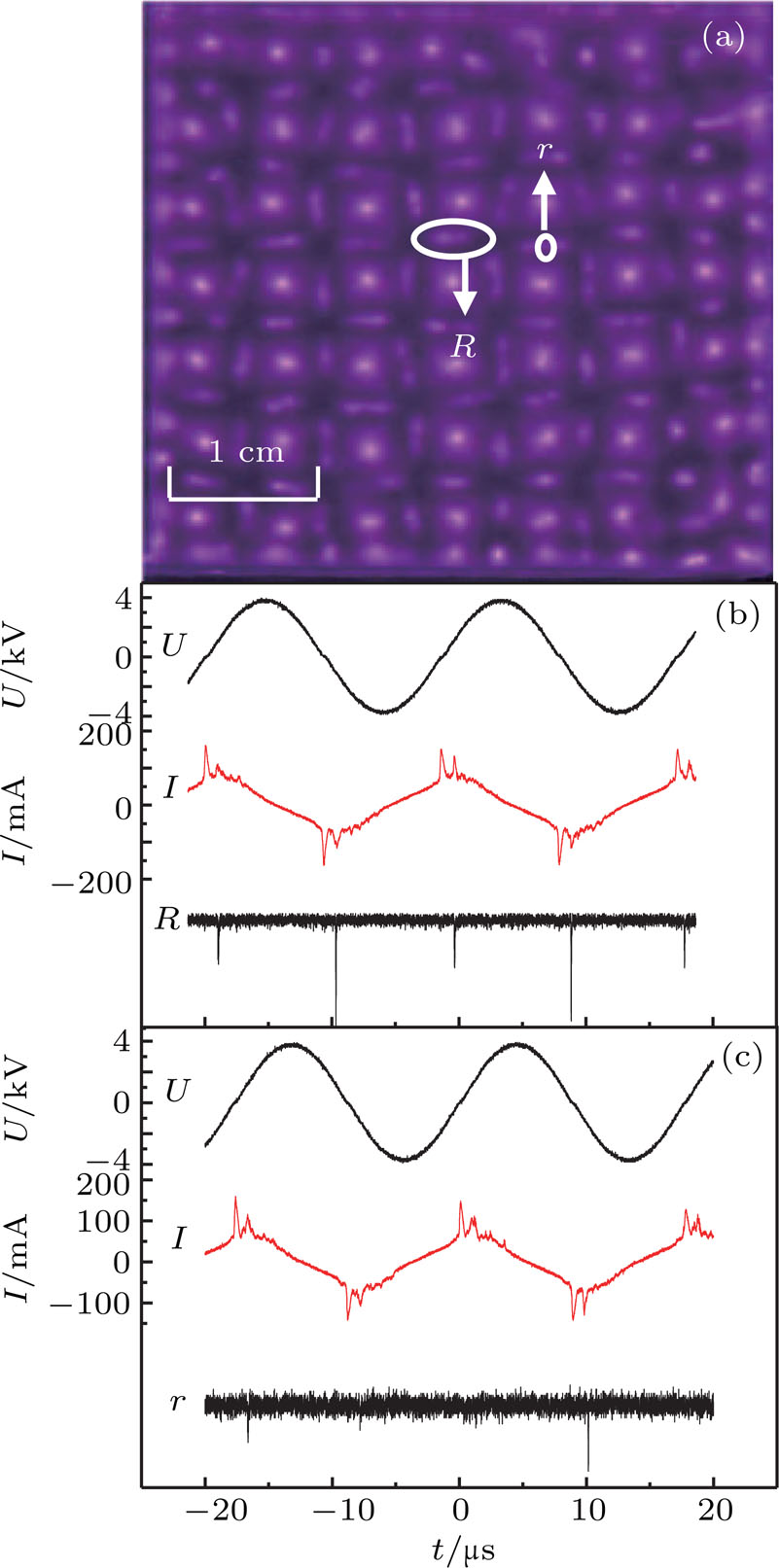
Figure 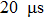

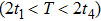
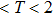
In the following, the forces exerted on one vibrating filament will be analyzed to interpret the interaction between vibrating filaments. Figure
The vibration of one filament affects the force of the surrounding filaments. Therefore, four vibrating filaments are considered as a cell to study the interaction of four vibrating filaments. The structure and dynamics of vibrating filaments are determined by both the potential energy and the mutual Coulomb repulsion of the vibrating filaments. The Coulomb interaction between the vibrating filaments depends on the wall charges of the vibrating filaments during the discharge. Since the large spots are discharged at the falling edge, the remaining wall charges are extremely small after the discharge is extinguished, and therefore the influence from the large spots on the vibrating filament can be ignored. Thus, the interaction and total energy between the four vibrating filaments can be expressed as follows:
In order to study the influence of antisymmetric stretching vibration on the formation of ASVSSP, we compare the distribution of electric fields with the square superlattice pattern observed by Dong’s group.[21] Figure
In conclusion, the influence of vibration on the spatiotemporal structure of the pattern is studied for the first time in DBD. The spatiotemporal dynamics of the ASVSSP is studied by an ICCD camera and a photomultiplier. The ASVSSP is an interleaving of three different sublattices. The discharge sequence of different sublattices is small rods, halos, and large spots in each half-voltage cycle, respectively. The small rods in the pattern are consisting of vibrating filaments. Based on the results of the HSVC and photomultiplier, it is concluded that the vibration mode of the vibrating filaments is a kind of antisymmetric stretching vibration. The vibration period T of the vibrating filaments with antisymmetric stretching vibration is 0.4 ms 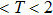
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] |