† Corresponding author. E-mail:
During a dc corona discharge, the ions’ momentum will be transferred to the surrounding neutral molecules, inducing an ionic wind. The characteristics of corona discharge and the induced ionic wind are investigated experimentally and numerically under different polarities using a needle-to-ring electrode configuration. The morphology and mechanism of corona discharge, as well as the characteristics and mechanism of the ionic wind, are different when the needle serves as cathode or anode. Under the different polarities of the applied voltage, the ionic wind velocity has a linear relation with the overvoltage. The ionic wind is stronger but has a smaller active region for positive corona compared to that for negative corona under a similar condition. The involved physics are analyzed by theoretical deduction as well as simulation using a fluid model. The ionic wind of negative corona is mainly affected by negative ions. The discharge channel has a dispersed feature due to the dispersed field, and therefore the ionic wind has a larger active area. The ionic wind of positive corona is mainly affected by positive ions. The discharge develops in streamer mode, leading to a stronger ionic wind but a lower active area.
A corona discharge is a self-sustained discharge that occurs in the vicinity of electrodes with smaller curvature radii.[1] It is often produced by applying high voltages on needle, wire, or tip electrodes. Because of the geometric effect, the electric field in the space presents remarkable non-uniformity and varies with the distance to the active electrode. During the corona discharge, ions are produced from the ionization process and accelerated by the field. The ions with the same polarity as the active electrode drift towards the ground electrode and transfer momentum to the surrounding neutral molecules. The induced fluid movement of all of the particles is so called ionic wind.
Benefiting from non-mechanical components, micro scales, and low costs, this electro-hydrodynamic (EHD) airflow has shown its great potential in applications such as ionizing blower,[2] thermal cooling,[3,4] and recently the flow control.[5,6] It is worth noting that recently Xu et al. reported a powered flight of an aeroplane whose propulsion is based on ionic wind induced by corona discharge.[7] Consequently, various investigations have been carried out on its performance.[8–10] Moreau et al. made a series of measurements on the velocity of ionic wind.[11,12] In their experiments, the corona discharge produced an ionic wind with a velocity up to 10 m/s under the discharge power of several mW. The behaviors of the ionic wind induced along the flat plate were also visualized by particle imaging velocimetry.[13] It was confirmed that the ionic wind has a great influence on the properties of surrounding airflow and provides an efficient drag reduction. In Kawamoto’s works, the influence of ionic wind was measured by the deformation of water surface. The calculated EHD force is on the order of 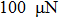
Theoretical and numerical investigations have also been carried out on the ionic wind.[16–20] Drews et al. established a theoretical model that describes the different characteristics of ionic winds in dc corona and ac corona.[21] The EHD process was considered using the momentum-transfer equation, flow continuity equation, and Navier–Stokes equation. Dau et al. simulated the EHD flow of an ionic wind device that includes two pin electrodes generating positive and negative corona respectively and generates nearly neutral wind flow using programmable open source OpenFOAM.[22] Most recently, Chen et al. presented a good understand on the ionic wind of negative corona by investigating its time-resolved and averaged characteristics in simulation and also studies the effect of dc voltage polarity on ionic wind experimentally for cooling purpose.[23,24] These works, to some degree, imply that the ionic wind phenomenon depends on the discharge polarity and regime, but the underlying physical mechanisms have not yet become clear. In particular, the ion dynamics and field distribution in negative and positive corona, which may lead to different discharge regimes or characteristics of ionic wind, need further study.
In this paper, we present the experimental and numerical investigation on the ionic wind induced in dc corona discharge. The electrical and mechanical characteristics are measured and compared under different polarities of the applied voltage. By using a fluid model, the development of discharge, as well as the generation of the EHD process is analyzed in detail. A theoretical consideration is made to explain the mechanisms of the ionic wind and the effect of the voltage polarities.
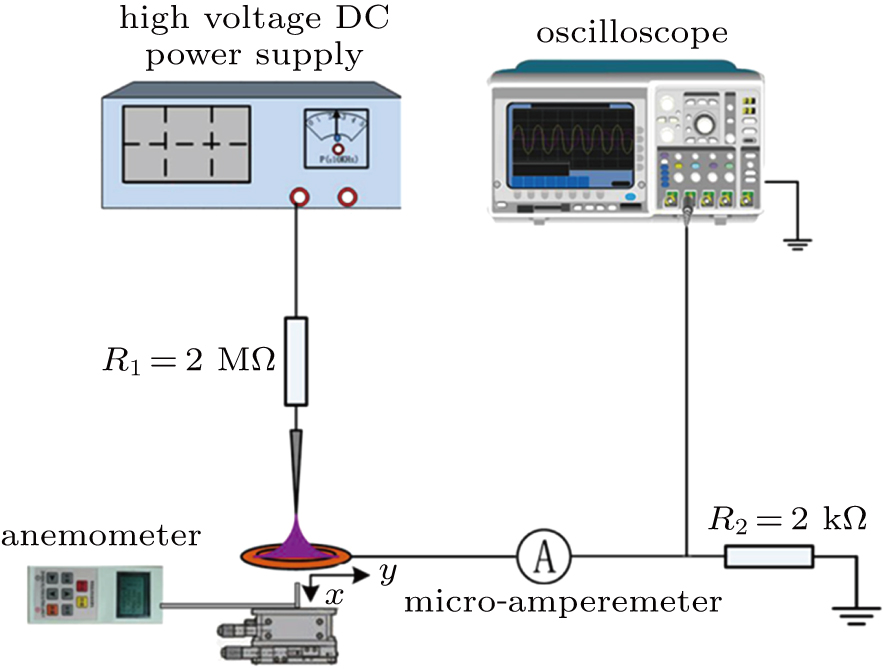
The experimental setup is schematically illustrated in Fig. 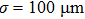




The corona discharge in the present configuration turns on when the inception voltage Vc is reached and then the ionic wind with the magnitude of m/s can be measured downstream the discharge part. The following experiment is conducted in ambient air with the temperature of 25 °C and the relative humidity of 30%.
During the negative corona, the development of discharge can be generally divided into three stages, as shown in Fig. 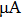
 | Fig. 2. (a) The V–I characteristics of negative corona at different d and (b) the corresponding discharge images in the sequence of current increasing under d = 5 mm. |
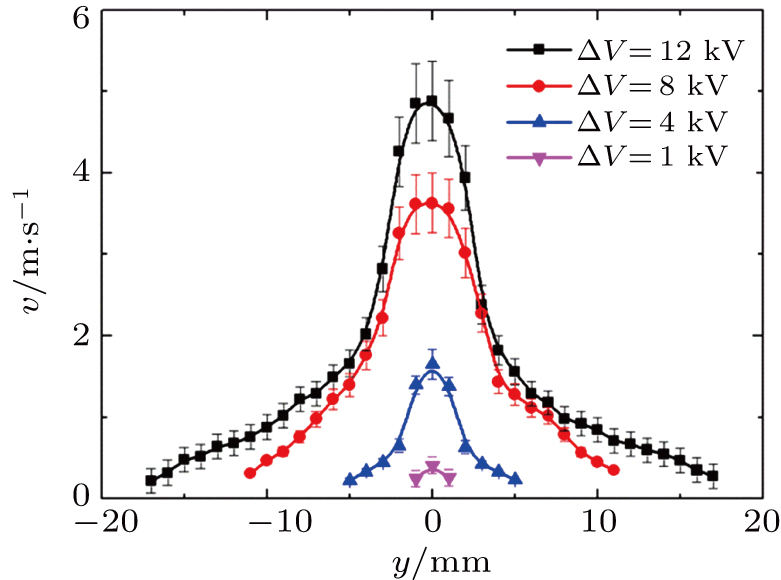
The measurements of the ionic wind velocity are made at x = 5 mm and y = 0 mm downstream the discharge part. The results are summarized in Fig. 
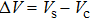



 | Fig. 3. Ionic wind velocity in negative corona at different d measured at x = 5 mm downstream the discharge part. |
Some previous studies also reported the investigations on the V–I and v–V characters, such as Figs.
Furthermore, the profiles of the wind velocity are obtained spatially by adjusting the location of the tube using the positioning platform. Figure 


The characteristics of positive corona are quite different from those of the negative one as previously reported.[1,2] Generally, the current waveforms of positive corona appear as a series of irregular narrow pulses instead of highly repetitive pulses (or Trichel pulses) in negative corona. The average current increases rapidly with the increasing applied voltage until sparks in experiment, as shown in Fig.
 | Fig. 5. (a) The V–I characteristics of positive corona at different d and (b) the corresponding discharge images in the sequence of current increasing under d = 20 mm. |
The v–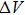
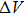

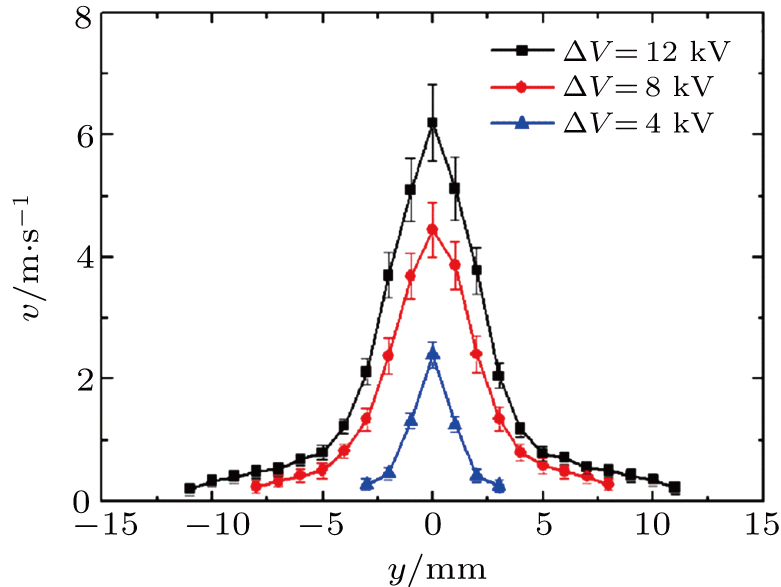
 | Fig. 6. Ionic wind velocity in positive corona at different d measured at x = 5 mm downstream the discharge part. |
In addition, the profile of the ionic wind in positive corona is quite different from that of the negative ionic wind, as shown in Fig. 
The EHD generation process of the ionic wind in both negative and positive corona is also investigated numerically using a 2D axis-symmetric fluid model. Major particles (N2, O2, 
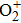

Considering that the negative ionic wind in applications often works under the voltage condition of the Trichel pulse stage, the simulation is conducted in the pulsed stage mainly. We here start with the spatiotemporal development of the negative corona discharge. In atmospheric air discharge, the density of 

In Fig. 
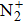
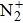



In Fig. 
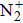

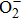
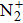
As can be seen in Figs.
Physically, the generation of the ionic wind is related to the spatiotemporal development of ion distribution and is described by the Navier–Stokes equation
 |
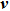

 |
Equation (
The distribution of the EHD force in the stable Townsend stage or in the glow stage is similar to that at the pulse initial time (see the case of t = 84 ns) or the pulse peak (see the case of t = 137 ns), respectively. Here, the description would not be repeated any more.
Then the time-averaged velocity of the ionic wind can be calculated by solving Eq. (
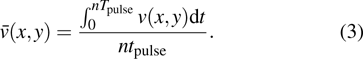 |


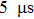
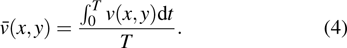 |
The EHD process in positive corona is also investigated using the present model. The discharge conditions are similar to those in the negative corona model and in experiment.
The positive corona propagates in streamer mode as successive positive ion clouds move towards the grounded electrode, which has been discussed in detail in classical works.[1] Each propagating cloud contributes a narrow pulse in the waveforms. Figure 
In the positive corona, due to the fact that electrons drift towards the needle anode, the negative ions, formed by neutral molecules absorbing electrons, generally have nothing to do with either the pulsed discharge or the formation of ionic wind. Consequently, the distribution of the EHD force varies with the movement of the positive clouds. The spatiotemporal development of the normalized EHD force is calculated using the method in Eq. (
At the beginning of the pulse (185 ns), the EHD force accelerates the flow mainly at the vicinity of the needle anode, where the positive cloud is gradually formed. Around the pulse peak, the positive cloud propagates to the grounded side and is strengthened by ionization (or the electron avalanches) through the discharge path. Therefore, the EHD force has a positive effect on the generation of the positive ionic wind in the most part of the discharge gap (215 ns). Then, the discharge current falls back and the positive cloud is absorbed by the grounded electrode. As a result, the force f(E) reduces and distributes mainly around the grounded part (290 ns). The discharge pulses in positive corona are irregular and generally the value of f(E) is positively associated with the pulse current, but the spatiotemporal distribution always follows the tendency described in Fig.
The time-averaged velocity of the ionic wind in positive corona is calculated by the integral of Eq. (
In the dc corona discharge, the electric field is sharply non-uniform due to the geometric effect. Two regions can be distinguished in the inter-electrode space.[11,15,21,31] The ionization region with a size of several millimeters in general locates at the vicinity of the active electrode, where the field is strong and the ionization process (or the electron avalanche) sustains. The second region, which is termed the drift region, locates from the ionization region to the grounded electrode. In the drift region, the field is insufficient to sustain the ionization and the ion drift is driven by the field. The momentum will be transferred to surrounding molecules through collisions, thus forming the ionic wind.
In the negative corona, the produced positive ions from ionization are attracted by the needle cathode and the electrons are driven towards the grounded electrode. In the drift region where the electric field is relatively low, the slow electrons will soon be captured by electron-negative molecules (i.e., O2 in air), forming the negative ions and then momentum transfer happens between negative ions and molecules. The electrons move along the diffused field and therefore the induced electron avalanches are dispersed from each other, as shown in Fig.
However, the direction of the field is reversed in the positive corona, as shown in Fig.
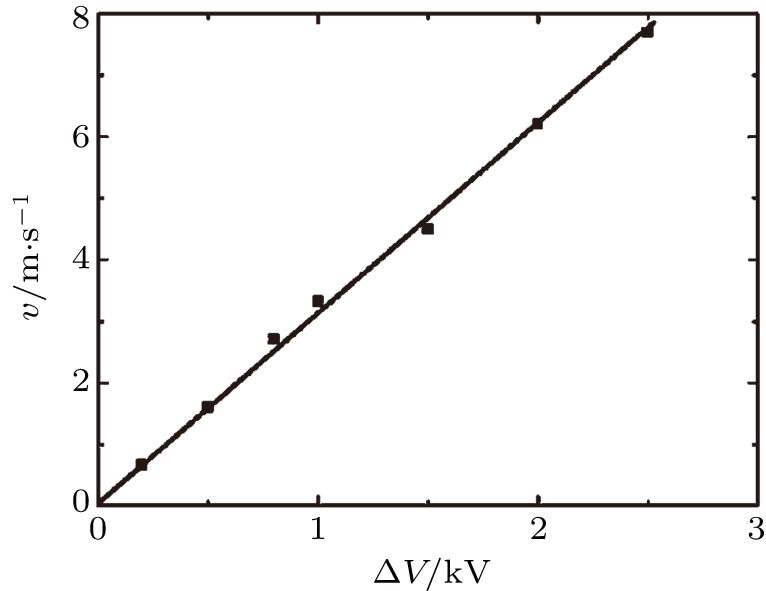
A brief discussion can be made on the relation between the wind velocity v and the overvoltage 
 |
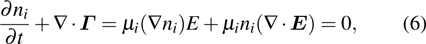 |
 |
 |
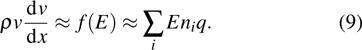 |
 |
The characteristics of ionic wind in dc corona discharge are investigated experimentally and numerically using the needle-to-ring configuration. In the present experiment, the averaged velocity and the distribution of the ionic wind are measured and compared under different polarities. The dynamics of the ions and the spatiotemporal distribution of the EHD force during discharges are simulated by a 2D axis-symmetric fluid model. Under negative and positive polarities, the mechanisms of corona and the induced ionic winds are different. The results are summarized as follows.
(I) The velocity of the ionic wind always increases lineally with the overvoltage in both kinds of polarities, but the velocity in the positive corona case increases faster than that in the negative corona case under similar conditions.
(II) The negative corona has a diffused morphology causing an ionic wind with a larger active area but a lower velocity. The positive corona propagated in streamer mode forms a straight discharge channel. The induced ionic wind has a relatively stronger velocity but a much smaller active area under the same overvoltage of negative corona.
(III) The spatiotemporal distribution of EHD force is different during the generation of the ionic wind under different polarities. The EHD force accelerates the negative ions mainly at the grounded side in negative corona discharge. However, in the positive corona, the positive ions are accelerated during their drift in the inter-electrode space.
(IV) The differences of characteristics between negative and positive ionic winds are caused by the different discharge mechanisms. The electron avalanches are dispersed from each other to induce a diffused-like discharge under negative polarity but converged towards the needle electrode, leading to propagation of positive ions and further the streamer mode under positive polarity.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |