† Corresponding author. E-mail:
A method of combining Green’s function retrieval theory and ultrasonic array imaging using Lamb waves is presented to solve near filed defects in thin aluminum plates. The defects are close to the ultrasonic phased array and satisfy the near field calculation formula. Near field acoustic information of defects is obscured by the nonlinear effects of initial wave signal in a directly acquired response using the full matrix capture mode. A reconstructed full matrix of inter-element responses is produced from cross-correlation of directly received ultrasonic signals between sensor pairs. This new matrix eliminates the nonlinear interference and restores the near-field defect information. The topological imaging method that was developed in recent ultrasonic inspection is used for displaying the scatterers. The experiments are conducted on both thin aluminum plates containing two and four defects, respectively. The results show that these defects are clearly identified when using a reconstructed full matrix. The spatial resolution is equal to about one wavelength of the selectively excited mode and the identifiable defect is about one fifth of the wavelength. However, in a conventional directly captured image, the images of defects overlap together and cannot be distinguished. The proposed method reduces the background noise and allows for effective topological imaging of near field defects.
The use of ultrasonic imaging for nondestructive testing (NDT) has been the subject of many investigations in recent years.[1] B-scan is the simplest method available with a transducer array. Imaging techniques derived from B-scan, such as spatial compounding technique,[2] synthetic aperture,[3] and synthetic aperture focusing techniques,[4] directly associate the arrival time of the ultrasonic waves with the defect positions in the medium. Other techniques, such as migration techniques[5] and time reversal techniques,[6] are based on prior knowledge of the wave propagation in the medium. Topological imaging is an emerging ultrasonic imaging method based on two wave field computations performed for the so-called reference medium.[7] This method relies on mathematical tools to create an image in an equivalent virtual domain from a set of experimental data. Topological optimize is a mathematical method that was first applied to optimize mechanical structures. The topological image will highlight all the differences between the investigated experimental medium and the reference medium. Defect imaging is achieved after an optimization process in which a cost function between the forward and adjoint problem is minimized, without prior assumptions of locations and shapes of defects.
The application of topological imaging in NDT started in the last decade. High resolution results have been presented for imaging scatterers using bulk wave inspection.[8–14] In the early stage, topological gradient was mainly used as imaging function,[8–11] because it directly influenced the change of cost function. However, the method required many times of iterations to achieve a high resolution. Subsequently, the researchers began to explore the use of other fast imaging methods, for instance, the time domain topological energy method proposed by Dominguez and Gibiat[13] and frequency domain topological imaging by Rodriguez and his co-authors.[14] Recently, the topological imaging has been extended to inspect the plate-like waveguide.[15,16] Rodriguez et al.[15] investigated guided wave topological imaging of isotropic plates based on propagation of the single S0 Lamb mode. Despite a high dispersion of S0 mode, scatterers were accurately located and the defect imaging was obtained with a spatial resolution of one wavelength. In contrast to classical and advanced delay and sum imaging method, topological method does not involve explicit computations of rays among emitters, defects, and receivers. The necessary information is implicit in the two wave field computations performed in the defect-free medium. Therefore, if wave propagation can be properly simulated in a given medium, then the defects of the medium can be imaged whatever the complexity of the propagation process. The topological method has also been applied to defect imaging in the anisotropic plates.[16]
Ultrasonic array imaging has been widely used in modern industrial NDT.[17] Each element of an array can be pulsed independently. The response of an ultrasonic transducer in pulse-echo operation contains nonlinear effects caused by physical limitations of acquisition systems (e.g., ultrasonic reverberation within the transducer) which obscure early time acoustic information.[18] The problem is exacerbated when using ultrasonic arrays in which the proximity of elements leads to saturation of neighboring elements through electrical and mechanical cross-talk. A solution to alleviate the nonlinear effect is to introduce a stand-off medium between the transducer and specimen, which reduces the acoustic energy transmitted to the specimen and the additional refracted modes that may induce imaging artifacts. Classical techniques for NDT purposes rely mainly on pitch-catch measurements of direct ultrasonic waves between an actuator and a receiver in the region to be measured. In this study, we propose an approach to retrieve the near field acoustic information through cross-correlation of directly received ultrasonic signals between sensor pairs.
It has been indicated theoretically and experimentally that the cross-correlation between signals recorded simultaneously at two points can provide an estimate of the Green’s function between two points.[19–24] Through this, a virtual array of emitters and receivers is formed. Hence, Green’s function is applicable for the retrieval of information obscured by the operating limitations of the acquisition systems. Early applications were in the fields of geo-physics and underwater acoustics.[19–21] Recently, researchers have applied this method for the purpose of structural diagnostics. Yang et al.[22] presented a characterization method by measuring Green’s function reconstruction from noise excitation and verified the feasibility of crack detection in poor noise source detection. Experimental investigations were undertaken to detect fatigue cracking due to variation of the cross-correlation function as a damage index between pristine state in low-amplitude excitation and the crack open-closure state. A fatigue crack introduced in an aluminum plate was successfully identified and oriented, proving that this technique was effective in detecting fatigue cracking from ambient noise. Duroux et al.[23] performed experimental study for damage detection in a thin aluminum plate with complex geometry. The experimental results of this study suggested that measuring the relative amplitude variations of the cross-correlation function of elastic diffuse fields could potentially provide a sufficiently robust tool for passive monitoring or imaging of a structural damage. Chehami et al.[24] presented an experimental validation of a passive technique for defect localization in metallic plates. A correlation matrix was estimated from noise vibrations recorded on a transducer array. A defect was localized by applying a beam forming algorithm to the difference between the correlation matrices obtained with and without the defect. They successfully detected defects for different kinds of noise sources. Sabra et al.[25] experimentally used the cross-correlation of ambient vibrations (CAV) technique in a high-speed naval ship for passive structural health monitoring. The influence of the ship’s operating conditions on the stability of the peak coherent arrival time was discussed.
This paper reports an approach of retrieval and imaging of near field defects using Lamb waves. The capacity of the proposed approach to identify near field defects is demonstrated experimentally on two aluminum plates containing two and four defects, respectively. This paper is organized as follows. Section
It has been shown in seismology that ensemble averaging the cross-correlation of responses recorded at two monitoring stations, the direct response between the stations is obtained. It is assumed that there is random noise source ri 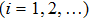
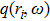
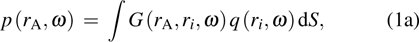 |
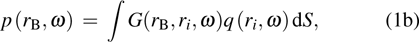 |
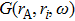
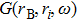
In an acoustic field, it is assumed that the noise sources are spatially distributed and uncorrelated. With the power spectrum 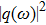
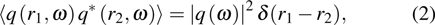 |
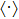
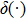
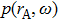
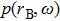
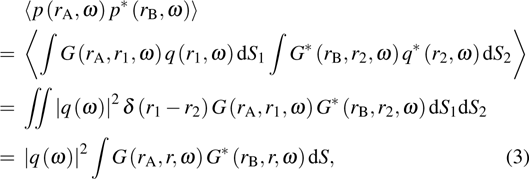 |
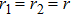
The following expression can be deduced:[26]
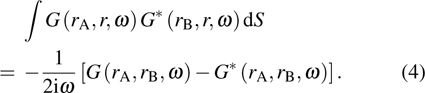 |
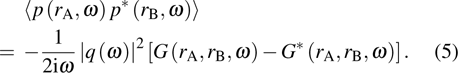 |
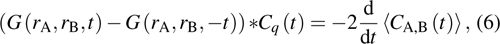 |
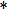
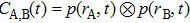
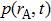
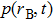
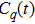
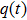
It is indicated from Eq. (
Full matrix capture is a process of sequential acquisition of responses for every transmitter–receiver transducer pair of ultrasonic array which are then collated to form the so-called full matrix.[27] Various post-processing approaches are developed to improve the imaging resolution.[28] Here, the time domain responses of the direct captured full matrix 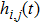
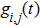
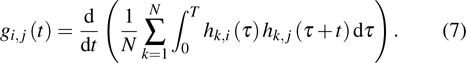 |
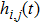
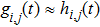
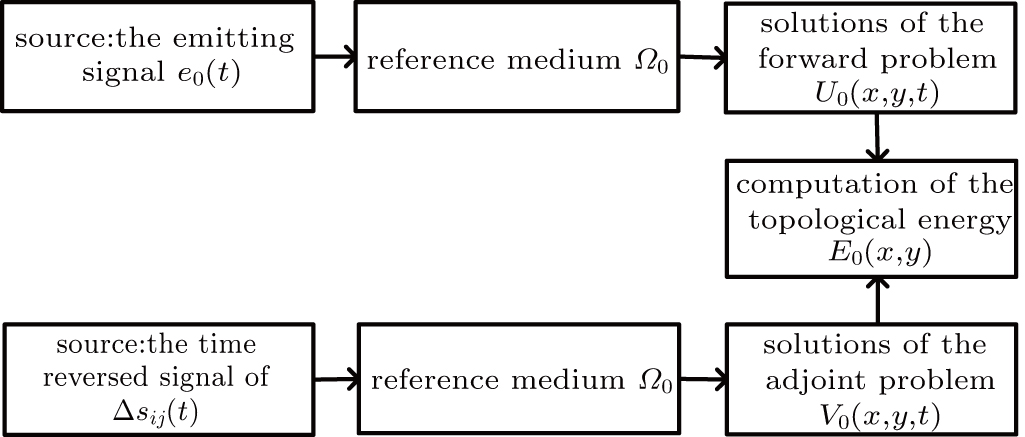
The topological imaging method defines two physical problems to be solved: the direct and the adjoint problem.[15] The solution of these problems corresponds to the simulation of the propagation of two different sets of waves emitted at the location of the array. In the direct problem, the experimental source is simulated. In the adjoint problem, the source is the time-reversed difference between the measured wave field and that obtained from the direct problem. The two field computations are performed in the defect-free medium. The topological image is computed by multiplying both wave fields together in the time or frequency domain, and integrating over the time or frequency. The work presents the application of time domain topological energy method (TDTE)[11,13] for nondestructive testing. The analytical method is used in the acoustic field simulation.
Considering two isotropic homogeneous bounded media, the first is defect-free (reference medium 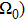
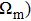
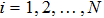
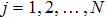
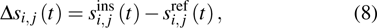 |
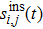
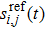
The forward and adjoint problems are solved according to Lamb wave propagating model. Let the exciton be 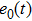
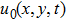
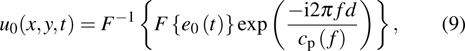 |
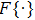
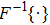
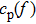
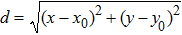
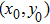
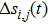
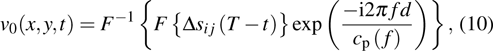 |
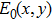
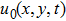
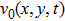
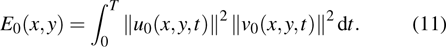 |
Measurements are carried out using an M2M MultiX LF system (M2M-NDT Co. Ltd, France). Two 1 mm thickness aluminum plates are investigated in this work. A 16-element linear array (Shantou Ultrasonic Electronics Co. Ltd, Guangdong, China) is used. The array is composed of 16 transducers each with a central frequency of 1 MHz. The transducer width is 1.8 mm and the pitch size is 2 mm. Thus, the whole array is 31.8 mm long. The height of the transducer is 15 mm. Similar to previous literatures,[15,16] the array is coupled to the plate on the edge so that it is sensitive to the in-plane motion, as shown in Fig.
 | Fig. 2. Experimental setup: (a) system configuration; (b) aluminum plate A with two defects; (c) aluminum plate B with four defects. |
The relative positions of the defects on the two inspected plates are specified in Fig.
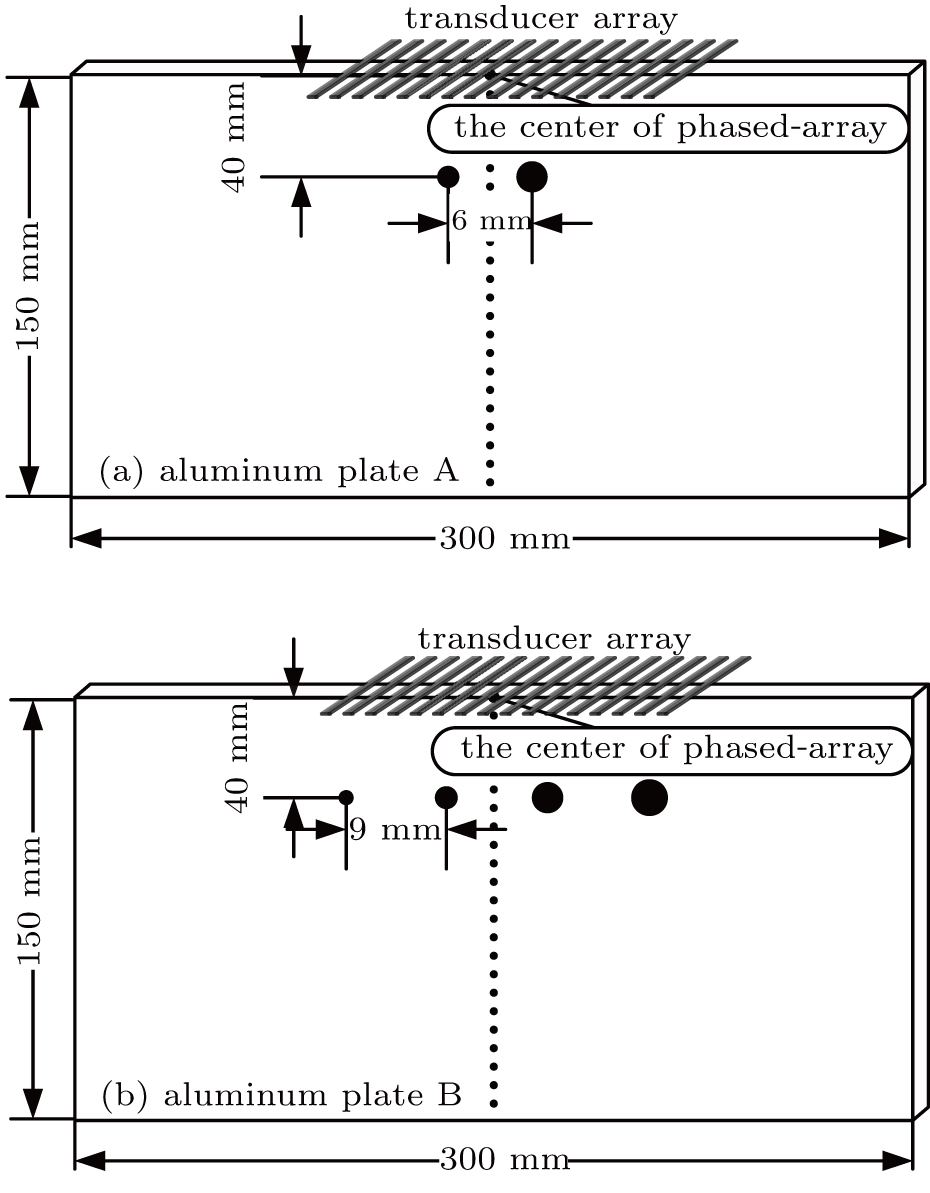 | Fig. 3. Schematic diagram of defects and transducers location: (a) aluminum plate A with two defects; (b) aluminum plate B with four defects. |
The excitation is a five-cycle Gaussian sinusoidal signal with a central frequency of 1 MHz. Such a signal covers the whole frequency bandwidth of the transducers. Considering the 1 mm thickness of the two plates, the frequency-thickness product is 1 MHz 
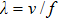
 |
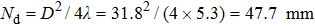
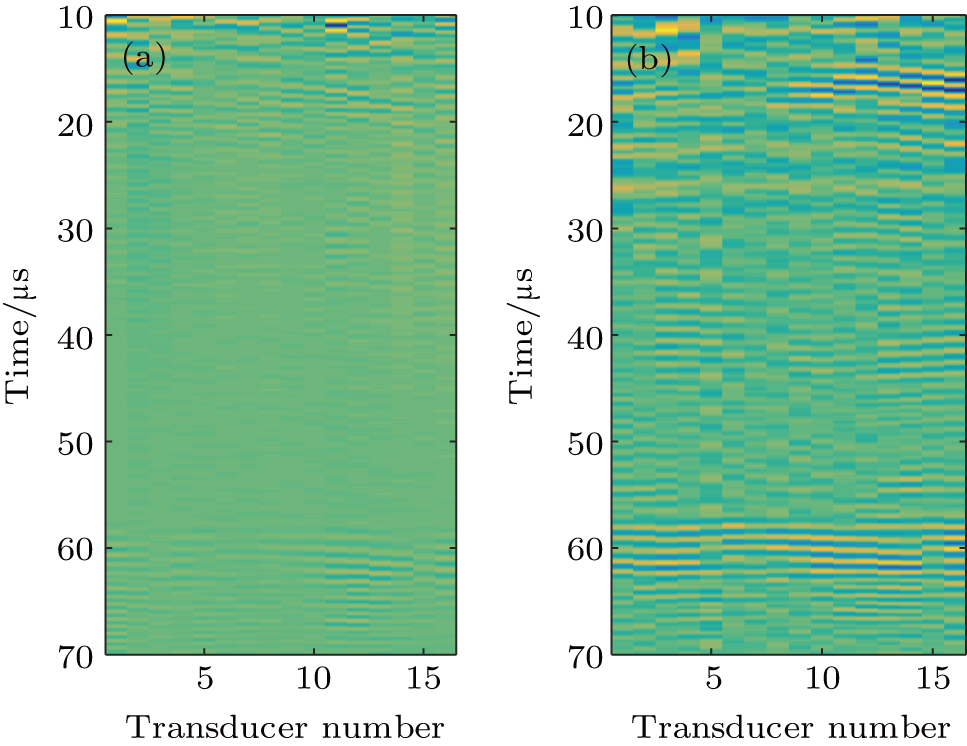
The emitting–receiving mode of the probe is set to the full matrix mode. The sampling frequency is 50 MHz. One of the transducers is used as an emitter and all of the transducers (including the emitter itself) record the Lamb wave signals. Thus, a 16 × 16 full matrix is captured. Two examples of typical time traces for i = 16, j = 12, of each full matrix for two plates are shown in Figs. 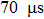
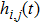
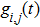
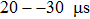
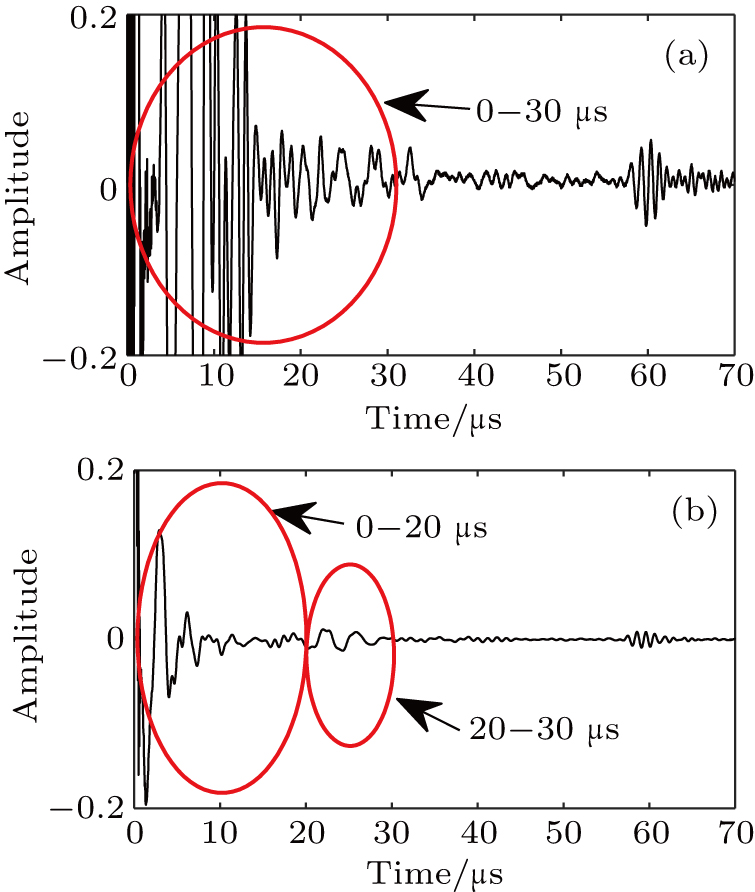 | Fig. 4. Time trace of i = 16, j = 12 for aluminum plate A: (a) directly captured; (b) reconstructed. |
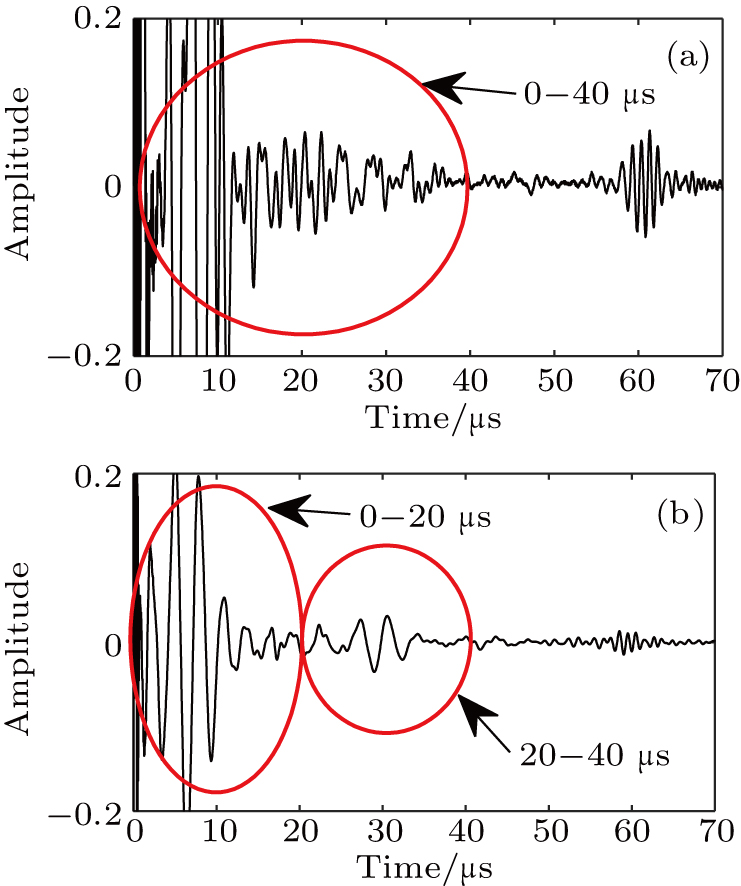 | Fig. 5. Time trace of i = 16, j = 12 for aluminum plate B: (a) directly captured; (b) reconstructed. |
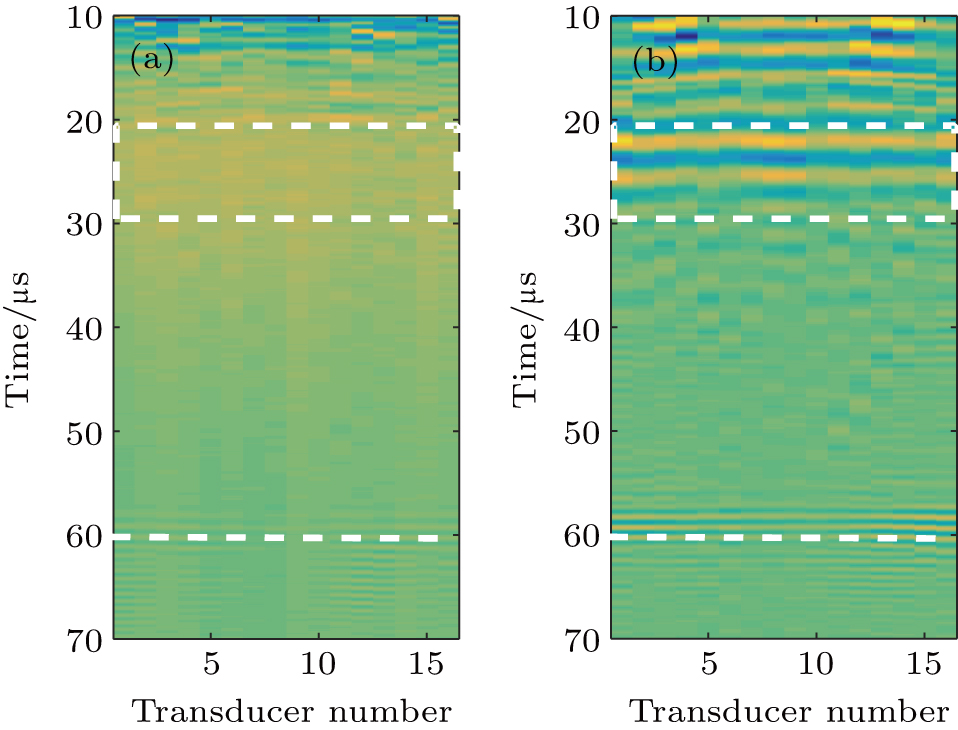 | Fig. 6. Pulse-echo responses of each element (i = j) for aluminum plate A: (a) directly captured; (b) reconstructed. |
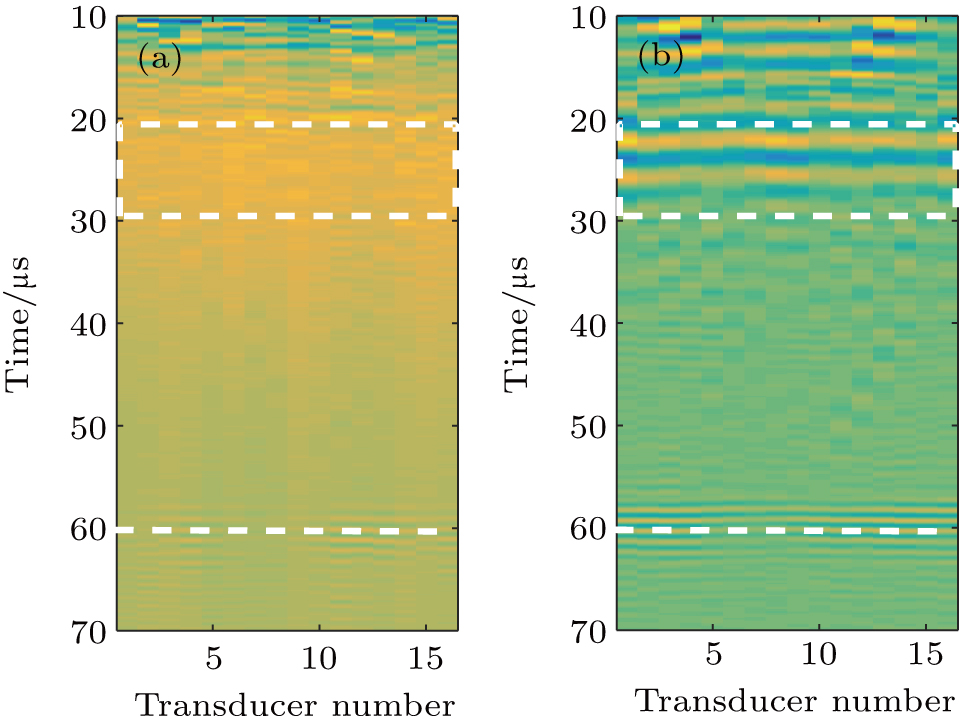 | Fig. 7. Pulse-echo responses of each element (i = j) for aluminum plate B: (a) directly captured 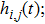
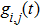
|
To quantitatively evaluate the processing effect of the reconstructed matrix, the signal to noise ratio (SNR) is calculated[32]
 |
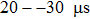
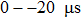
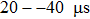
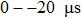
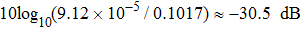
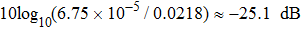
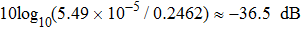
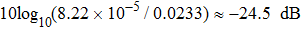
In terms of this calculation, the SNR of the reconstructed full matrix is obviously improved, which demonstrates the feasibility of the proposed method.
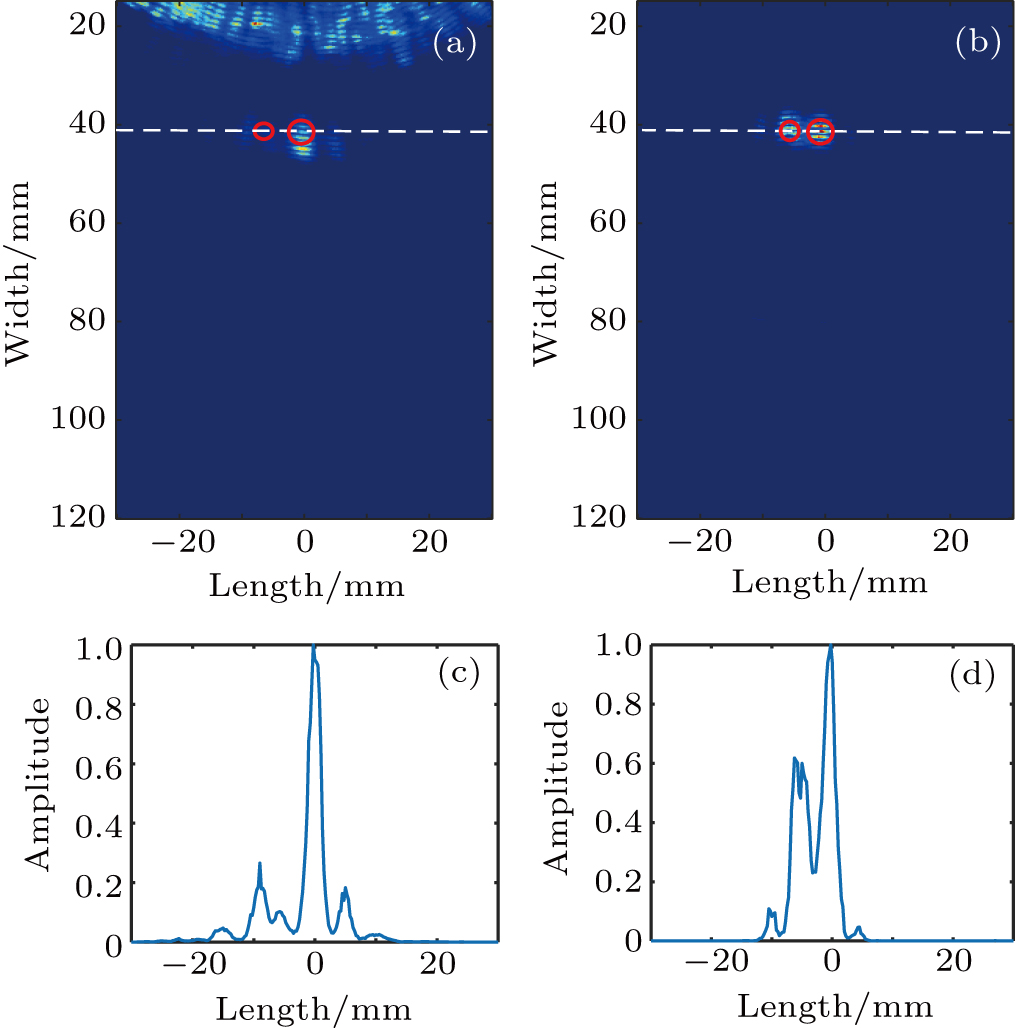
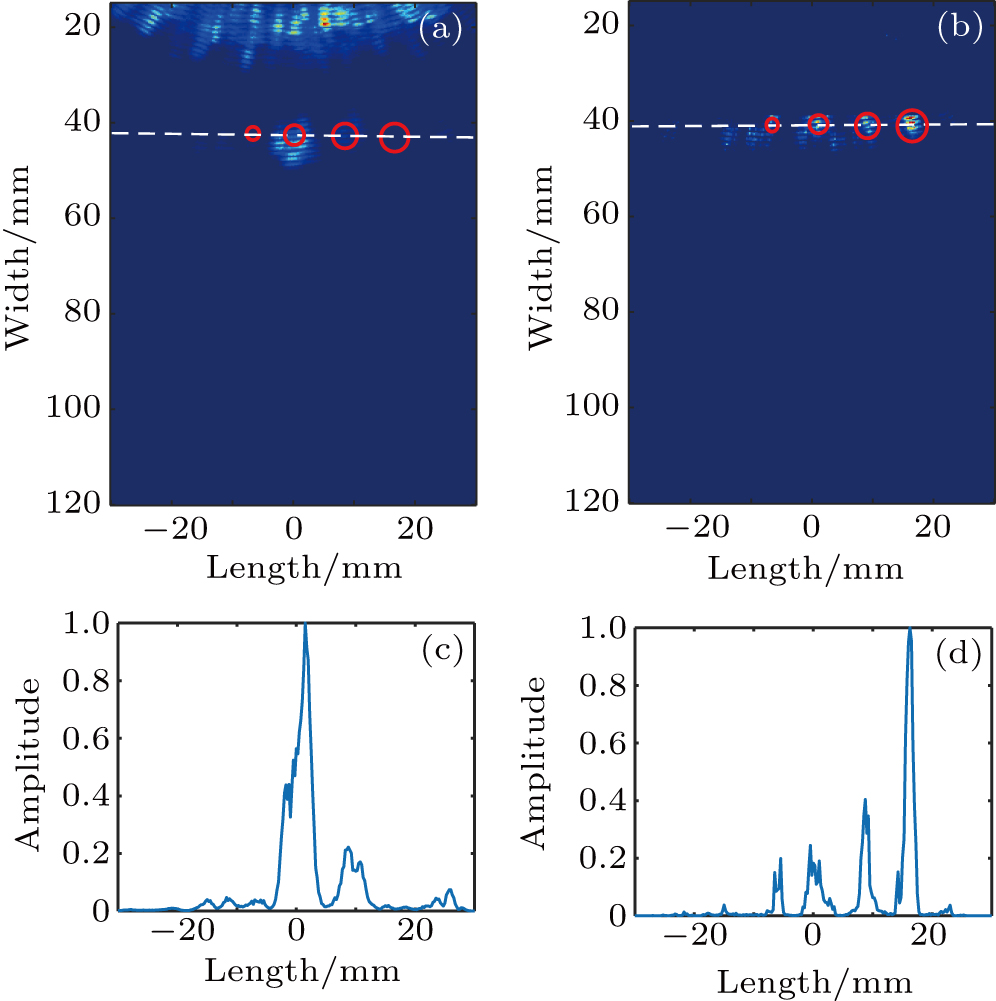
It has been observed that although the defects in aluminum plate A and B are different, the B-scan images of the two plates are visually similar, especially for Figs.
Topological images generated using directly captured and reconstructed full matrices for two inspected specimens are shown in Figs.
In this paper, we have applied the Green’s function retrieval theory and Lamb wave topological imaging method to discern near field defects in thin aluminum plates. Near field acoustic information is obscured by nonlinear effects of instrument acquisition system. The theory demonstrates that a full matrix can be reconstructed through cross-correlation of directly received ultrasonic signals between sensor pairs. The new matrix restores the near-field defect information without acquisition artefacts. Experiments are undertaken to detect both aluminum plates containing near filed defects with different sizes. Compared to the conventional directly captured full matrix, the SNR of the reconstructed full matrix is improved by more than 5 dB. Furthermore, topological imaging shows that the aliasing holes in a conventional directly captured topological image can be clearly resolved when using the reconstructed full matrix. The spatial resolution is equal to one wavelength of the selectively excited S0 mode and the identifiable defect is about one fifth of the wavelength. The results demonstrate that the method based on Green’s function reconstruction is effective for near field defect imaging from directly contact ultrasonic measurement.
To show the great potential of Green’s function retrieval and topological imaging of near field defects to inspect large plate-like structures, the results presented in this paper have been preliminarily limited to monomodal excitation and isotropic media. Since the presented method is in essence based on information processing and wave field computation, there is no theoretical obstacle in applying the method to anisotropic media, such as the detection of fatigue cracks and depressions in flying bodies or multimodal guided wave inspection. These new investigations are now in progress.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |