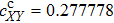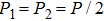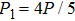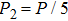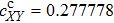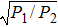The study of the propagations of optical beams in nonlocal nonlinear media has aroused a large amount of interest during recent years, both theoretically^[1–11] and experimentally.^[12,13] The nonlocality refers to that the response of the medium to the input light at a particular point is not solely determined by the optical intensity at that point but also depends on the intensity around it. According to the relative width of the response function and the optical beam, there are four categories of the nonlocality;^[3] that is, local, weakly nonlocal, generally nonlocal, and strongly nonlocal. In particular, the strong nonlocality is just the case when the characteristic nonlocal length is much larger than the beam width. For this special case, the evolutions of a spatial optical beam can be described by the Snyder–Mitchell model,^[1] which is a linear model and has an exact Gaussian-shaped stationary solution called as an accessible soliton. Various kinds of spatial solitons can be supported by nonlocal nonlinear media, such as Hermite–Gaussian solitons, Laguerre–Gaussian solitons,^[14,15] Ince–Gaussian solitons,^[16] dipole solitons,^[17] spiraling elliptic solitons,^[18,19] and spiraling elliptic Hermite–Gaussian solitons,^[20] just to name a few. Specifically, the spiraling elliptic solitons carry the orbital angular momentum (OAM) and can rotate in the transverse, which can form in the isotropic nonlinear media due to an effective anisotropic diffraction resulting from the OAM.^[18,19] It is shown that spiraling elliptic soliton is the lowest-order mode of spiraling elliptic Hermite–Gaussian soliton,^[20] and for the latter it exhibits n holes aligning along the direction of the principal axis of ellipse for the n-th order mode.

A vector soliton occurs when more than one field are involved.^[21,22] In general, the vector soliton is absent of any interference between the single components by using different polarizations or different wavelengths. Vector solitons can also exist in nonlocal nonlinear media.^[23–25] Very recently, we have shown that the polarized vector spiraling elliptic solitons can be supported by the nonlocality of nonlinear media.^[26] We demonstrate that a Gaussian beam can induce an equivalent refractive waveguide of the circular symmetry, in which a spiraling elliptic soliton forms, with no special requirement of the optical power for the latter. In this paper, we will investigate the spiraling elliptic Hermite–Gaussian soliton propagating in such an equivalent refractive index waveguide induced by the orthogonally polarized Gaussian beam. Furthermore, we will also discuss the nonlinear coupling effects in the weak nonlocality, where the refractive index waveguide loses its circular symmetry.

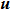
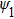
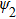
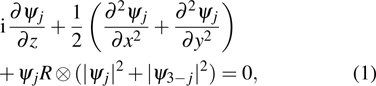The vector nonlocal nonlinear Schrödinger equation, which describes the propagation of the (1+2)-dimensional polarized vector beam in nonlocal nonlinear media, can be decomposed into two arbitrary orthogonal polarization components denoted as and ^[27,28]

The first component of the vector beams considered here is the spiraling elliptic Hermite–Gaussian beam^[20]

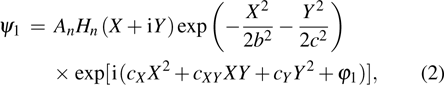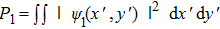
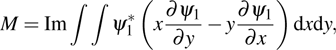If the response function is twice differentiable at x = 0, the nonlocal nonlinear Schrödinger equation (1), in the strong nonlocality case, can be simplified to the strongly nonlocal model

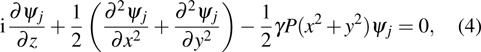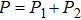
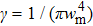
The Lagrangian density of Eq. (4) is expressed as^[30,31]

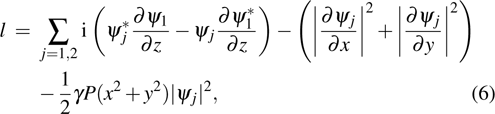The strongly nonlocal model in Eq. (4) shows that in strongly nonlocal case, the total power P of the vector beam contributes to the refractive index waveguide. This means that the two components of the vector beams experience the total power rather than their respective power. For the vector solitons, the requirement of yields the relations between two axes b and c of the spiraling elliptic Hermite–Gaussian soliton, and the beam width w of the Gaussian soliton is

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Evolutions of vector solitons during one period. The parameters are set as wm=15, b=1.5, c = 1, w=1.1767, , and the optical power P1 and P2 of two components are half of the total power P, that is, .

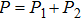
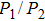
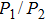
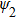
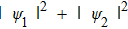
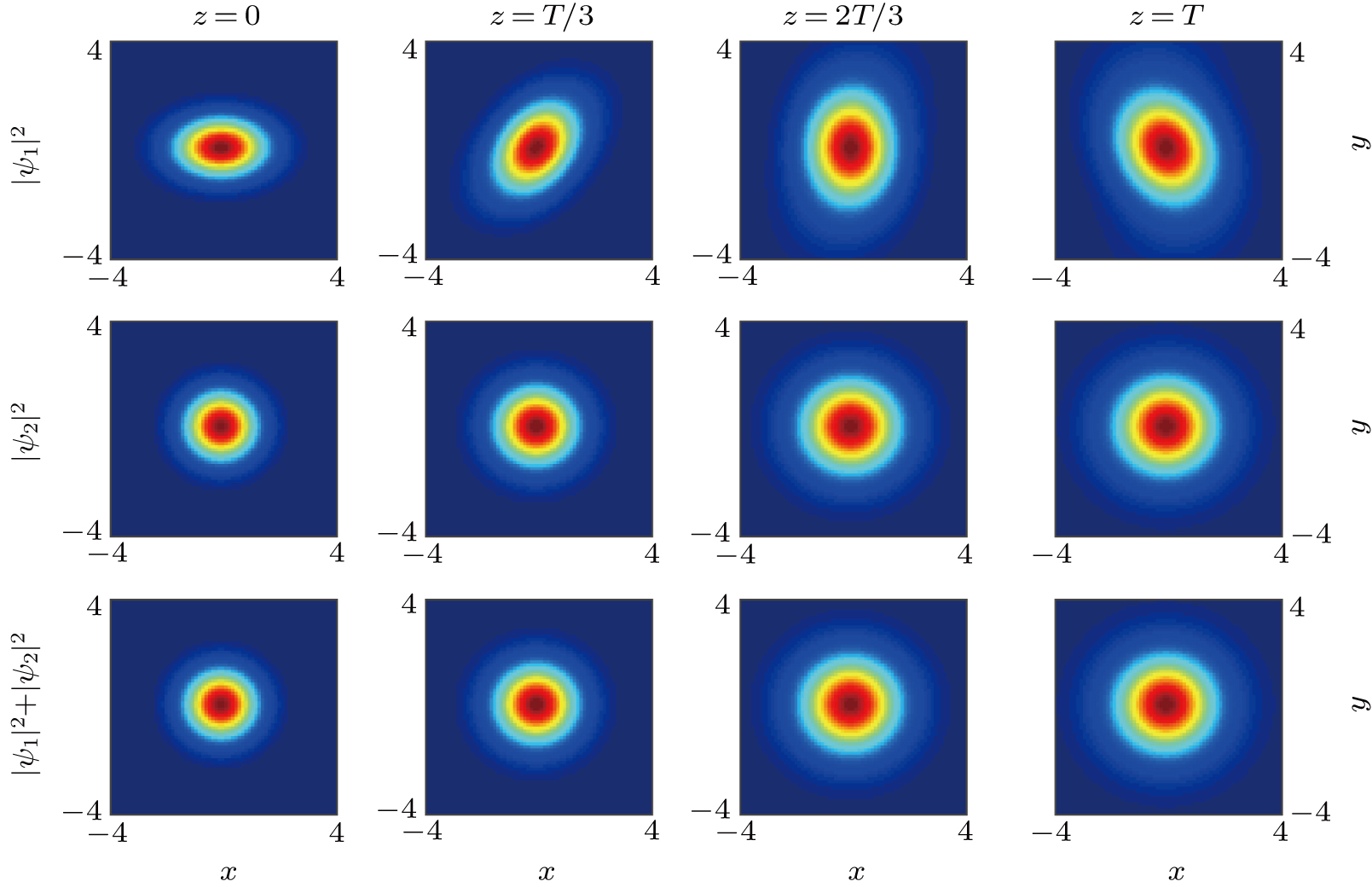
We should note that vector solitons form when is equal to the critical total power P_c, but regardless of the ratio of , which is set as 1 in Fig. 1, and 4 in Fig. 2. However, for different ratios of , both the spiraling elliptic Hermite–Gaussian beam and the fundamental Gaussian beam exhibit different intensity peaks, which results in different structures of the overall intensity , which can be found by comparing Fig. 1 with Fig. 2. The vector solitons comprising of the second-order spiraling elliptic Hermite–Gaussian soliton and the Gaussian soliton can also be supported by nonlocal nonlinearity, which is shown in Fig. 3.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Same as Fig. 1 except for and .

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Vector solitons of the second-order spiraling elliptic Hermite–Gaussian soliton and the Gaussian soliton. The parameters are set as wm = 30, b = 1.5, c = 1, w = 1.1767, , and the optical power P1 and P2 of two components are half of the total power P, that is, .

So far, we have discussed the strong nonlocality of the nonlocal nonlinear Schrödinger Eq. (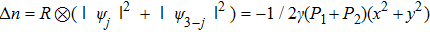1), and in this case the nonlinear coupling effects of the two constituent beams can be reflected by their contributions to the nonlinear refractive index in a linear manner; that is, . It is obvious that the nonlinear refractive index exhibits a circularly symmetrical profile in despite of the elliptic shapes for spiraling Hermite–Gaussian beams. Figure 4 shows the coupling effects by simulating the nonlinear propagation of the spiraling elliptic Hermite–Gaussian beam with and without the fundamental Gaussian beam.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Same as Fig. 1 except for and .

The cases for weak nonlocalities will be quite different, as shown later. Substitution of the spiraling Gaussian beams in Eq. (2) with n = 0 and the Gaussian beam in Eq. (4) into the convolution of the nonlinear refractive index yields

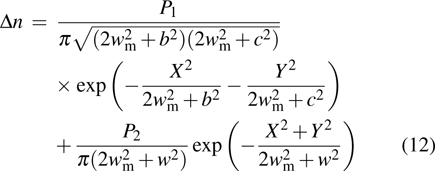The different contribution to the nonlinear refractive index from the fact that will be smoothed out when the degree of nonlocality σ increases, and be enhanced when σ decreases. Furthermore, the profiles of the nonlinear refractive in Eq. (12) do not depend on the ratio between two powers P₁ and P₂ for the strong nolocality limit that . However, when (σ decreases, the different power ratio will result in different profiles of the nonlinear refractive in Eq. (12). For the large ratio of , will tend to exhibit an elliptic profile, and a small ratio of will make more circularly symmetrical, as shown in Fig. 5.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Profiles of the nonlinear refractive along X (red curves) and Y (blue curves) directions for amplitude power ratio , that is, 50, 1, and 1/50 in the left, middle, and right panels. Other parameters are set as wm = 2, b = 2, c = 1, and w is given by Eq. (11).

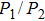
The discrepancy of along the X and Y directions can be made more obvious by increasing the difference between two semi-axes b and c of the elliptic beam and decreasing the value of w_m. Still, the nonlinear refractive lacking circular symmetry in weak nonlocality plays an important role on both components of the vector beam. First, the ellipse shaped refractive index “waveguide” forces the Gaussian beam in Eq. (4) to lose its initial circular symmetry as shown in Fig. 6, where the beam has a ratio defined by and .

Fig. 6.

	Figure Option ViewDownloadNew Window
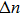
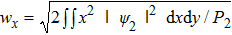
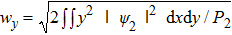
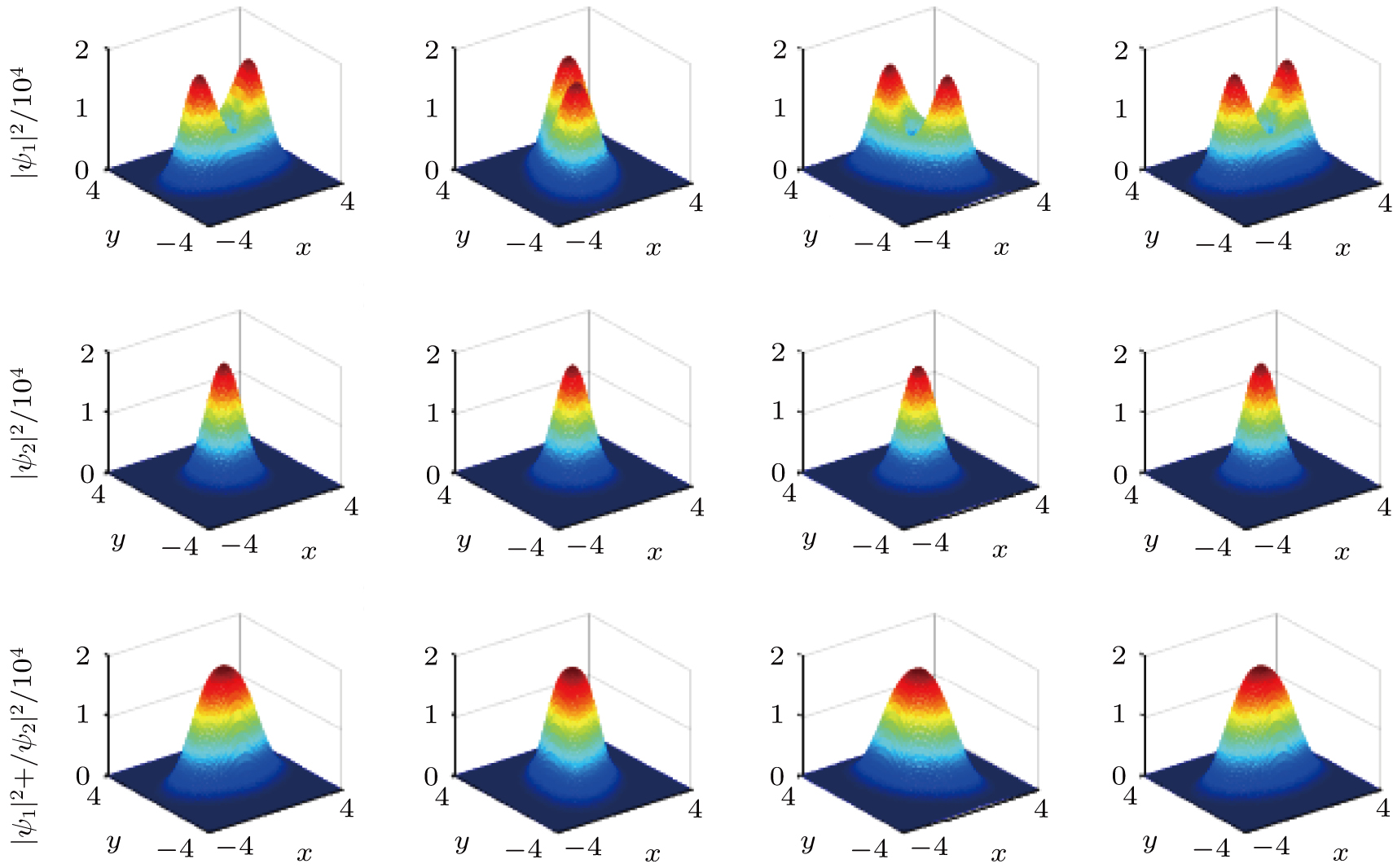
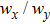
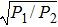
	Fig. 6. Evolution of beam with a ratio for the Gaussian beam in Eq. (4) for different amplitude ratios of . Other parameters are set as wm = 2, b = 1.5, c = 1, and w is given by Eq. (11).

As can be seen from Fig. 6, when the contribution to the nonlinear refractive in Eq. (12) from spiraling Gaussian beams in Eq. (2) dominates, the initial circular Gaussian will change to an elliptic Gaussian. Furthermore, it should be noted that the ellipse shaped refractive index “waveguide” described by Eq. (12) is expressed in rotating coordinate system XYZ, and rotates with the propagation distance in the xyz coordinate system. In the first stage, the refractive index aligns its major and minor axis along the x and y directions, respectively, which will cause the beam width w_x to exceed w_y for the Gaussian beam in Eq. (4). After the rotation of for some propagation distance, the major and minor axes will switch, and then w_y will become larger than w_x for the Gaussian beam. The different power ratio of also has an effect on the evolution of the spiraling Gaussian beams in Eq. (2), which is shown by the comparison between Figs. 7 and 8.

Fig. 7.

	Figure Option ViewDownloadNew Window
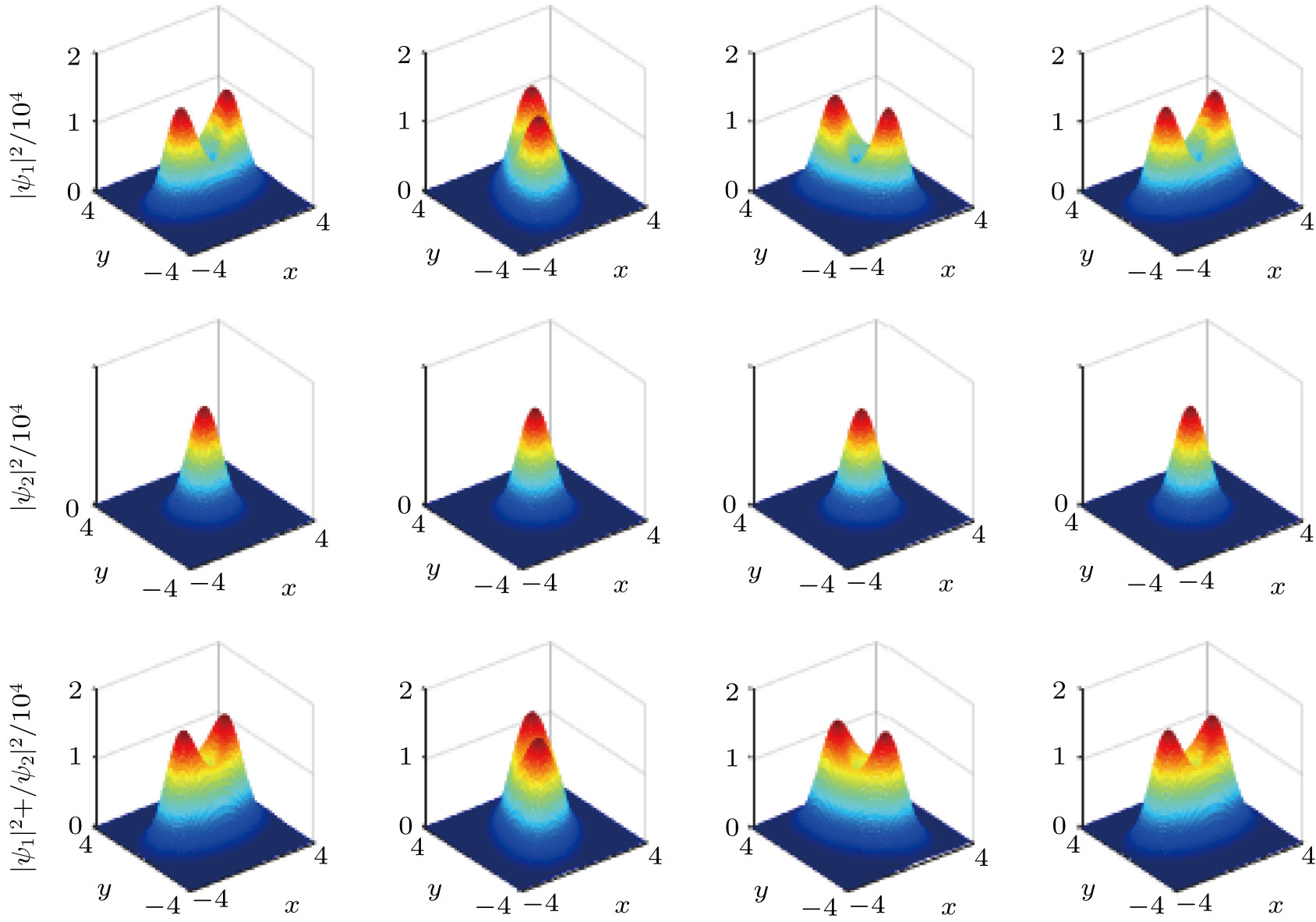
	Fig. 7. Evolutions of vector solitons in weak nonlocality when wm = 2. Other parameters are set as b = 1.5, c = 1, w = 1.1767, 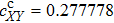, and the amplitude ratio is assumed to be 50.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Same as Fig. 6, and the amplitude ratio is assumed to be 1/50.

It can be found that in the weak nonlocality, the rotational speed is smaller compared with the strong nonlocal case. In one period , the spiraling beam can not recover its initial intensity profile. We can explain this damping rotation as follows. In the weak nonlocality case, the optical beam will radiate both its power and OAM.^[32] The reduction of OAM leads to the slow reduction of rotational speed of the transverse rotating profile. While the reduction of the optical power will break the balance between the linear diffraction and the nonlinear focusing. Therefore, an obvious beam expanding can be observed in the propagation shown in Figs. 7 and 8. In addition, when we decrease the proportion of the spiraling elliptic component of the vector beam while keeping the total power invariant, the radiation of the OAM will be suppressed and the rotation due to the OAM will increase a little bit, which is shown in the first rows in Figs. 7 and 8.

The propagations of incoherent beams with two orthogonal polarizations in nonlocal nonlinear media are analytically discussed by variational approach. The vector beam is composed of a fundamental Gaussian beam and a spiraling elliptic Hermite–Gaussian beam carrying the orbital angular momentum. We obtain the critical power and the critical OAM required for the vector spiraling elliptic Hermite–Gaussian solitons. We find that the critical power, the critical phase-cross-product-term coefficient, and the rotational velocity are the same for any-order spiraling elliptic Hermite–Gaussian soliton. By changing the relative power ratio of the two components of the vector beam, the total intensity structure can be controlled. In the weak nonlocality region, the nonlinear refractive index loses its circular symmetry, and the nonlinear coupling effect is observed. Due to the radiation of the OAM, the damping of the rotation is predicted and can be suppressed by decreasing the proportion of the spiraling elliptic component of the vector beam. An obvious beam expanding is found to result from the radiating power in the propagation.