† Corresponding author. E-mail:
Synchronization is a phenomenon that is ubiquitous in engineering and natural ecosystems. The study of explosive synchronization on a single-layer network gives the critical transition coupling strength that causes explosive synchronization. However, no significant findings have been made on multi-layer complex networks. This paper proposes a frequency-weighted Kuramoto model on a two-layer network and the critical coupling strength of explosive synchronization is obtained by both theoretical analysis and numerical validation. It is found that the critical value is affected by the interaction strength between layers and the number of network oscillators. The explosive synchronization will be hindered by enhancing the interaction and promoted by increasing the number of network oscillators. Our results have importance across a range of engineering and biological research fields.
In recent years, complex system science has become a popular area of scientific research. Many phenomena in complex systems can be abstracted into complex networks for research, such as the operation of organisms, the cascading failures of power grid, and the blocking of Internet.[1,2] However, the interactions between the constituent elements and dynamic behaviors of complex systems are complicated, especially when they involve biology, sociology, computer science, and statistical physics.[3–5] Synchronization is one of the important dynamic behaviors, and has attracted a great deal of attention, especially the mechanisms generating synchronization and the control methods have become a major focus of research.[6,7] At present, several oscillator models are proposed to study synchronization, such as Kuramoto model, FitzHugh–Nagumo model, and Lorenz oscillator model.[8–11] In particular, the Kuramoto model is a classical phase model composed of kuramoto oscillators, which plays an important role in investigating the synchronization behavior of networks. Therefore, the corresponding analysis methods have also been proposed, such as the mean field method,[12] self-consistent analysis,[13] Ott–Antonsen ansatz, etc.[14,15]
Many researchers have found that the phase transition process of synchronous is a continuous process to synchronization.[16–19] However, this phenomenon was challenged in the scale-free network composed of Kuramoto oscillators, where the phase transition process was proved to be a discontinuous process when the natural frequencies of the Kuramoto oscillators and the degrees of the nodes are positively correlated. This abrupt transition from an incoherent state to a synchronous state in the complex network is named explosive synchronization (ES),[20] and it has opened up a whole new field of research on synchronization. Li et al.[21] studied the influence of network topology on ES, and found that ES occurs when the degree of node is positively correlated with the natural frequency. Leyva et al.[22] researched the ES on the complex network model with weights. Recently, Zhang et al.[23] proposed a single-layer frequency-weighted model of Kuramoto oscillators and observed the ES in general complex networks. They obtained the critical coupling strength 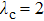
Although many related works on ES have been published, these works are all based on single-layer networks. In recent years, the research of synchronization on complex network has gradually shifted from the single-layer network to the multi-layer network. The interaction between layers should be considered because one network always interacts with other networks, such as the interdependence of client system and server system in computer network;[29] and the interaction control of communication network and power grid in electric power infrastructure.[30] Some related works of synchronization in multi-layer networks have been reported.[31–35] Among them, Su et al.[32] found that the strength of the inter-layer affects ES in the two-layer co-evolutionary networks. Zhang et al.[33] observed the phenomenon that the synchronous process changes from the first order phase transition to the second order phase transition in multi-layer networks. However, these works on ES in multi-layer networks are mainly investigated through numerical verification, while no rigorous theoretical analysis has been given. Therefore, the theoretical research of ES is challenged in multi-layer networks of Kuramoto oscillators, and how to build an appropriate Kuramoto model is a significant topic. In this work, we present a multi-layer frequency-weighted coupled Kuramoto model based on two-layer networks, in which two subnetworks are connected one-to-one. A rigorous theoretical analysis by mean field method and self-consistent theory is provided to obtain the critical coupling strength of ES in the two-layer networks. We analyze the influence of ES between layers and verify the theoretical results by numerical simulation.
This paper is organized as follows. In Section
For a frequency-weighted model of N Kuramoto phase oscillators on a single layer network, the evolution of each oscillator follows[23]
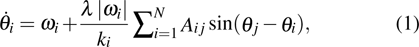 |
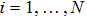
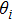
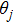
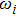
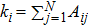
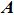
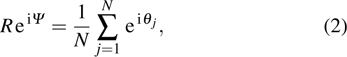 |
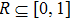
We consider a frequency-weighted Kuramoto model on a two-layer one-to-one connected complex system, as shown in Fig. 
 |
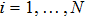
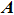
 |
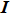
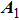

To simplify the research, we consider the multi-layer networks composed of the globally connected networks, and the natural frequency distributions of the two-layer network oscillators are the same symmetric bell curve distribution 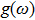
 |
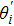

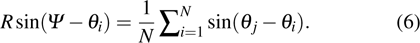 |
 |
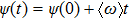
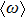
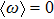
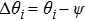
 |
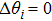
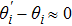
 |
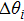
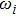
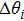
 |
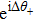
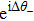
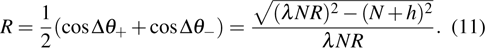 |
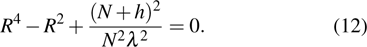 |
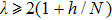
 |
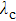
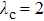
 |
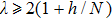

To verify the correctness of the theoretical results, we simulate the synchronization behavior of the two-layer frequency-weighted coupled complex system. The two-layer complex network is composed of the globally connected networks, and the natural frequency distribution follows the Lorentzian distribution 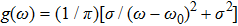


 |
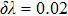
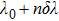
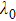

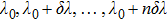
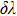
Figure 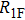

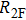


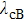
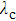
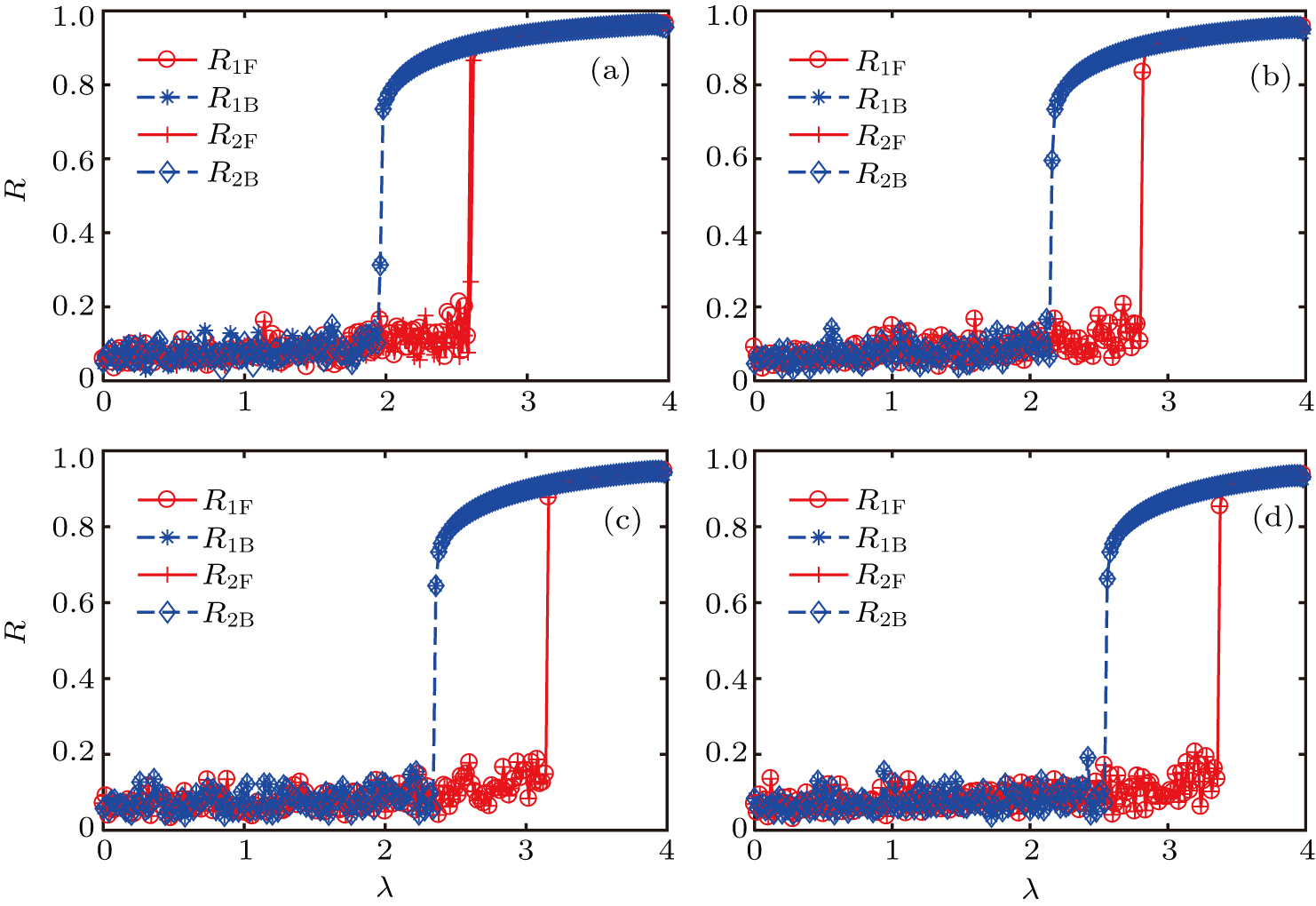 | Fig. 2. Synchronous phase transition diagrams of order parameters for different inter-layer interaction strengths ((a) h = 0, (b) h = 20, (c) h = 30, (d) h = 60) when N = 200. |
To emphasize the theoretical results, we show the relationship between the critical coupling strength 



 | Fig. 3. Comparison of theoretical results and numerical simulations of critical coupling strength variation with inter-layer interaction strength. |
| Table 1.
Error γ between the theoretical |
Through the previous theoretical analysis, we can also find that the critical coupling strength is affected by the number of network oscillators N. To further analyze the evolution of the oscillator’s collective behavior, we compute the oscillator’s effective frequency of one layer along the backward process as 

In Figs. 

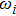



Similarly, to verify that the simulation results are consistent with the theoretical results, we give the relationship between 
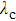
 | Fig. 5. Comparison of theoretical results and numerical simulations of critical coupling strength variation with network oscillator number. |
| Table 2.
Error γ between the theoretical |
Critical coupling strength is one of the key parameters that determinate the ES in multi-layer complex networks where the interaction between layers plays an important role. In this paper, we propose a frequency-weighted coupled model of Kuramoto oscillators and investigate the ES in the multi-layer networks. Through mean field method and rigorous self-consistent theoretical analysis, a critical coupling strength that ES appears on the multi-layer networks has been given. It is demonstrated that the critical coupling strength is determined by the inter-layer interaction strength and the number of network oscillators. Enhancing the interaction strength between layers will hinder the generation of ES and increasing the number of network oscillators will promote it. These conclusions are supported by both theoretical analysis and the matching numerical simulation results. It is a very significant research and has impacted on the generation and control of multi-layer complex systems in the real-world.
In this paper, we only analyze the multi-layer networks composed of fully connected networks. What happens if the topology of networks is non-fully connected, and what is the influence of node degree on the ES are left as open questions. Given that the impact of node degree and topology on ES in multi-layer networks remain unsolved, we will study them in our further work.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] |