Recently, event-based online social services, such as Plancast and Eventbrite, have experienced rapid growth. From these services, researchers observe a new type of social network, which makes it possible to combine virtual and physical social interactions. Figure 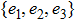1 depicts the constructing principle of EBSN based on the online social services data. In Fig. 1, A, B, C, and D represent four users of Plancast services, and are the events that these users participate in. The social relationships between users in Plancast service in Fig. 1(a), forming the online network of the Plancast EBSN, are mapped to green links of Fig. 1(b). Meanwhile, the same events that users co-participate in Plancast service in Fig. 1(a), deriving their offline social connections, collectively form an offline social network in the Plancast EBSN, denoted as blue edges in Fig. 1(b).

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. An example of event-based social service and its corresponding EBSN: (a) the Plancast service, and (b) its corresponding Plancast EBSN.

In this study a multi-layer network is constructed by utilizing the Plancast data, and the constructing principle is shown in Fig. 2. In Fig. 2(a), every user can participate in many different events, while one event can be participated by multiple users. For example, are the events that user A participates in, and e₁ is also participated by user B. A toy model of the special multi-layer network is shown in Fig. 2(b). The Plancast is divided into the online and offline layers. In the online layer, A, B, C, D, and E represent five users. If two users are friends, then there is an edge between them. The offline layer is composed of user events, while the dotted line indicates the corresponding relationship between online users and their event chains.^[28–30]

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. A schematic illustration of a multi-layer network: (a) the relationship between users and their events in Plancast service, and (b) its corresponding toy model of a special multi-layer network. The online layer represents the social relationship between friends, and the offline layer indicates the chain of events that they participate in.

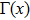
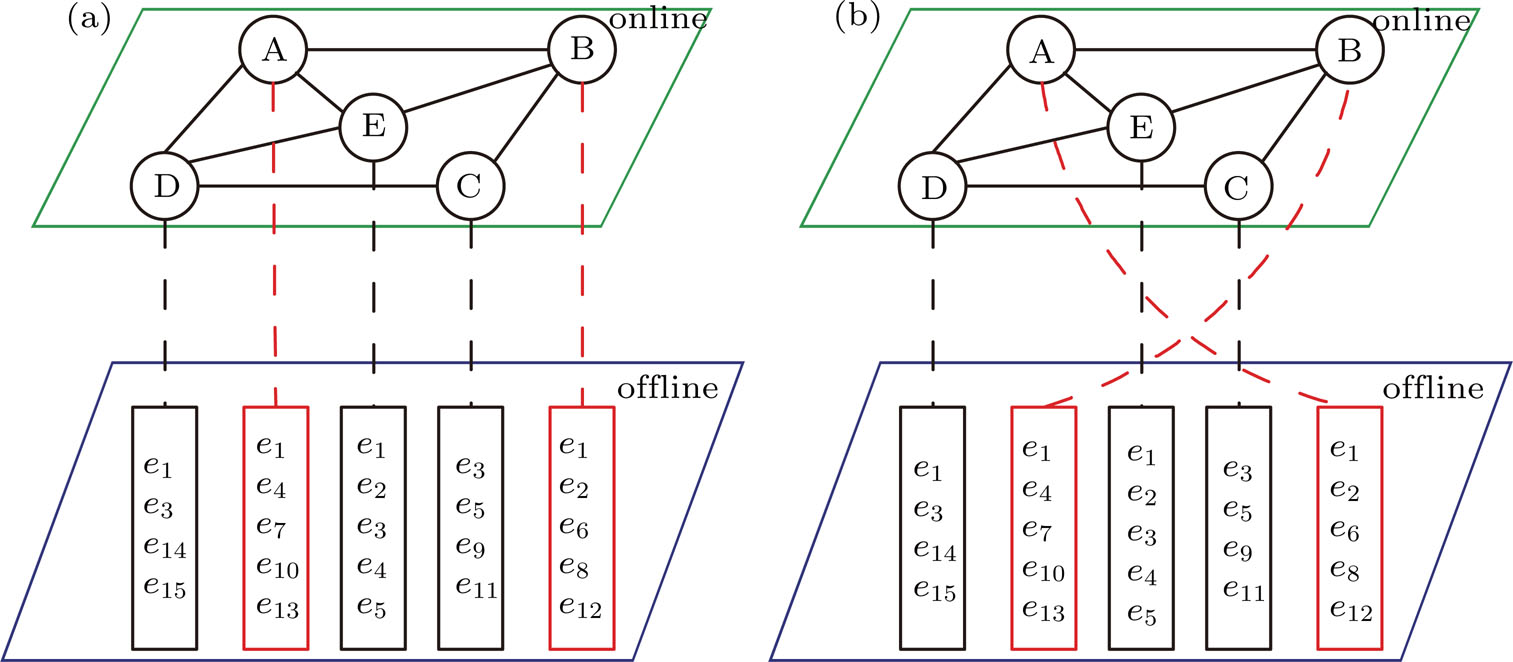
If two users are involved in more events together, then they will be considered to be more similar. In recent years, researchers have developed a number of indexes to measure similarity, such as Jaccard index, Hub Depressed Index (HDI), and Hub Promoted Index (HPI).^[26,27] These are common indexes in analyzing user similarity. For a node x, let k_x represent the degree of x and denote the set of neighbors of x. The definition of Jaccard, HDI, and HPI are as follows: 1 2 3

Like conventional online social networks, EBSNs provide an online virtual world where users exchange thoughts and share experiences. What distinguishes EBSNs from conventional social networks is that EBSNs also capture the effect of face-to-face social interactions in participating events in the offline physical world. To study the relationship between online social proximity and offline event similarity, we introduce two kinds of null models, which can not only change offline event chains but also maintain the social relationship in online social networks.

The construction of the null model of exchanging trajectory is shown in Fig. 3. Two users from all users are randomly selected. Then, the two event chains of users are obtained. Finally, the offline event marked by them is interchanged. For example, we randomly select two users A and B, and obtain their events in Fig. 3(a), and then we interchange the event chain marked by them. The result of the reconnection is shown in Fig. 3(b), in which the events of A are changed to , e₂, e₆, e₈, and the events of B are changed to , e₄, e₇, e₁₀, . The process of randomly rewiring should be repeated until a completely randomized null network is gained.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Constructing the null model of exchanging trajectory: (a) the original toy model, and (b) its corresponding null model of exchanging trajectory.

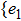
The construction of the null model of exchanging user events is shown in Fig. 4. The first step is the same as the null model of exchanging trajectory. Then, we obtain the event chains of two users and the number of events that users participate in, respectively. Finally, we randomly select events which have the same number as the original two users from all the events to them respectively. For example, two users A and B are randomly selected, and then we obtain that A has five events , e₄, e₇, e₁₀, and B has five events , e₂, e₆, e₈, , and all of the event information contain 9 events. Finally, we randomly select five events from all the events to A and randomly select five events to B. The result of the reconnection is shown in Fig. 4(b), and three events , e₆, of A and four events , e₇, e₁₀, of B are different from their original events. The process of randomly rewiring should be repeated until a completely randomized null network is obtained.

Fig. 4.

	Figure Option ViewDownloadNew Window
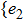
	Fig. 4. Constructing the null model of exchanging user events: (a) the original toy model, and (b) its corresponding null model of exchanging user events.

The null model of exchanging trajectory does not change the order of the event sequence but shuffles the ownership of the whole trajectory for each user. The null model of exchanging user events not only changes the ownership of a whole trajectory but also shuffles the set of events belong to each user. Both null models can change the offline event characteristics, and detect the correlation between offline events similarity and online social proximity. This correlation plays an important role in coordinating online and offline resources, such as recommending offline events based on online relationships.

In this study, the indexes above-mentioned (Jaccard, HDI, and HPI) have been applied and the results are similar. HPI is more observable, so the result of event similarity is shown by HPI in this study. The HPI distribution of the original network and its null models of exchanging trajectory are shown in Fig. 5(a). The blue-dotted line representsthe HPI distribution of the original network, and the grey lines indicate the results of 100 null models of exchanging trajectory. To demonstrate the experimental results more clearly, we compute the average HPI value of 100 null models and expressedthe HPI distribution with the square line. All ofthe HPI distribution of null models are less than that of the original network because this type of null model changes the belongingness of the original event chains. The results indicate that there is a strong correlation between online social relationship and offline event similarity. The same method is used to get the HPI distribution of the original network and null models of exchanging user events, which is shown in Fig. 5(b). We obtained the same conclusion as the null models of exchanging trajectory.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (a) HPI distribution of null models of exchanging trajectory and (b) HPI distribution of null models of exchanging user events. The x coordinate represents HPI values, and the y coordinate represents the probability of HPI values.

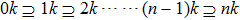
The 0k null network is the simplest and most randomized null model, which only possesses the same number of nodes and the average degree as a given graph . Here, V represents the set of nodes, and E represents the set of edges. The average degree refers to the average value of all the nodes’ degrees. Suppose n ( ) as the number of nodes and m ( ) as the number of edges, and the definition of the average degree is as follows: 4 While constructing the 0k null network for EBSN, the links in the offline network remain unchanged while those in the online network should be shuffled. For example, we randomly select a link C–D in the original network and disconnect it as shown in Fig. 6(a). We then randomly select two nodes C and E. If the two nodes are not connected, we then connect them. The result of the reconnection is shown in Fig. 6(b). The process of randomly rewiring should be repeated until a completely randomized null network is achieved.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. The constructing process of the 0k null network. We remove link C–D, then add link C–E in the online network: (a) the original toy model, and (b) its corresponding 0k null network.

The 1k null network possesses the same degree distribution (or sequence) as the original network. The degree distribution refers to the probability of nodes’ degree in the original network. If 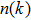is the number of nodes with degree k, then the degree distribution is defined as 5 While constructing the 1k null network of EBSN, links in the offline network remain unchanged while those in the online network should be shuffled. For example, referring to the constraints of generating 1k null network, we randomly select two links A–D and C–E in the online network and disconnect the links as shown in Fig. 7(a), and then we connect A–E and C–D. The result of the reconnection is shown in Fig. 7(b). The process of random rewiring should be repeated until a completely randomized null network is obtained.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. The construction process of the 1k null network. We remove links A–D and C–E, and then add links A–E and C–D: (a) the original toy model, and (b) its corresponding 1k null network.

The 2k null network possesses the same joint degree distribution as the original network. The joint degree distribution refers to the number of degree values (probability) of the nodes connected at both ends of each edge. Suppose that k represents the degree of a node and that is the total number of edges of the nodes whose degrees between k₁ and k₂. If , otherwise, . The joint degree distribution is 6 While constructing the 2k null network of EBSN, links in the offline network remain unchanged while those in the online network should be shuffled. The steps of the 2k null network are the same as those of the 1k method, except that the degree value of four nodes which are connected by the two edges is required to remain the same before and after shuffling. For example, as shown in Fig. 8(a), only when nodes D and E have the same degree value can the edge exchanging be carried out to ensure that the joint degree distribution of the whole network remains unchanged. We disconnect two links A–E and C–D, and we then connect A–D and C–E. The result of the reconnection is shown in Fig. 8(b). The process of randomly rewiring should be repeated until a completely randomized null network is achieved.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. The construction process of the 2k null network. We remove links A–E and C–D, and then add links A–D and C–E: (a) the original toy model, and (b) its corresponding 2k null network.

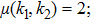
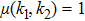
The 3k null network possesses the same joint edge-degree distribution as that of the original network, which means the same number of open triangle and close triangle exists between the original network and its 3k null network. The joint edge-degree distribution takes into account the interconnectivity between three nodes, mainly in two cases: the first is an open triangle where three nodes are connected by two edges, which is called the second is a closed triangle where three nodes form a ring, which is called .

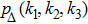
While constructing the 3k null networks, links in the offline network remain unchanged while those in online network should be shuffled. Two edges are randomly select in the original network to ensure that the joint degree distribution remains the same; that is, the basic properties of the 2k characteristics remain the same. The number of open triangle and close triangle for each node on both ends of two links and its neighbor nodes are then calculated before and after shuffling, respectively. If the numbers are the same, then we can conclude that the shuffling is successful. For example, referring to the constraints of generating the 3k null network, we disconnect two edges A–B and C–D. If the pairs of nodes A–D and B–C are not connected, then we connect them. The result of the reconnection is shown in Fig. 9(b). The process of randomly rewiring should be repeated until a completely randomized null network is obtained.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. The construction process of the 3k null network. We remove links A–B and C–D, and then add links A–D and B–C: (a) the original toy model, and (b) its corresponding 3k null network.

The HPI distribution of the Plancast network and its 0k–3k null networks are shown in Fig. 10. The red quadrilateral line represents the HPI distribution of the original network, and the grey lines denote the results of 100 null networks. To make the experimental results more clear, the average HPI values of the 100 null networks is computed and we give the HPI distribution in the black-star line.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. The impact of online social micro-structures on offline event similarity. The HPI distribution of (a) 0k null networks, (b) 1k null networks, (c) 2k null networks, and (d) 3k null networks.

We find that the HPI distribution of 0k and 1k null network are less than that of the original network. Compared with 0k and 1k null networks, the HPI distribution of 2k null networks are very close to the original network because they maintain more micro-scale structure characteristics of the original (i.e., assortativity). Furthermore, the HPI distribution of 3k null networks are more similar to that of the original network because 3k null networks keep the clustering characteristic of the original. These results suggest that the average degree (0k characteristic) and degree distribution (1k characteristic) are not enough to maintain event similarity between friends,but assortativity (2k characteristic) and clustering coefficient (3k characteristic) are significant micro-scale structures to maintain event similarity between friends.

Studies on network structure characteristics can help us to reveal the nature of complex systems, and the relationship between network structure and its function. Therefore, more researchers are devoting themselves to study the diversity of network structures.^[25,31] Actually, the number and subgraph structure of common neighbors are the important indexes to reflect the structural characteristics of social networks.^[24] However, these two factors have different effects on real networks in existing studies. For example, the researchers in ^[31] have shown that the number of common neighbors has greater impact on the similarity of network structure. In contrast, it is found in ^[25] that the number of common neighbors has no influence on social networks while the subgraph structure of common neighbors has a positive influence. In this chapter, we study the influence of these two factors on offline event similarity between friends.

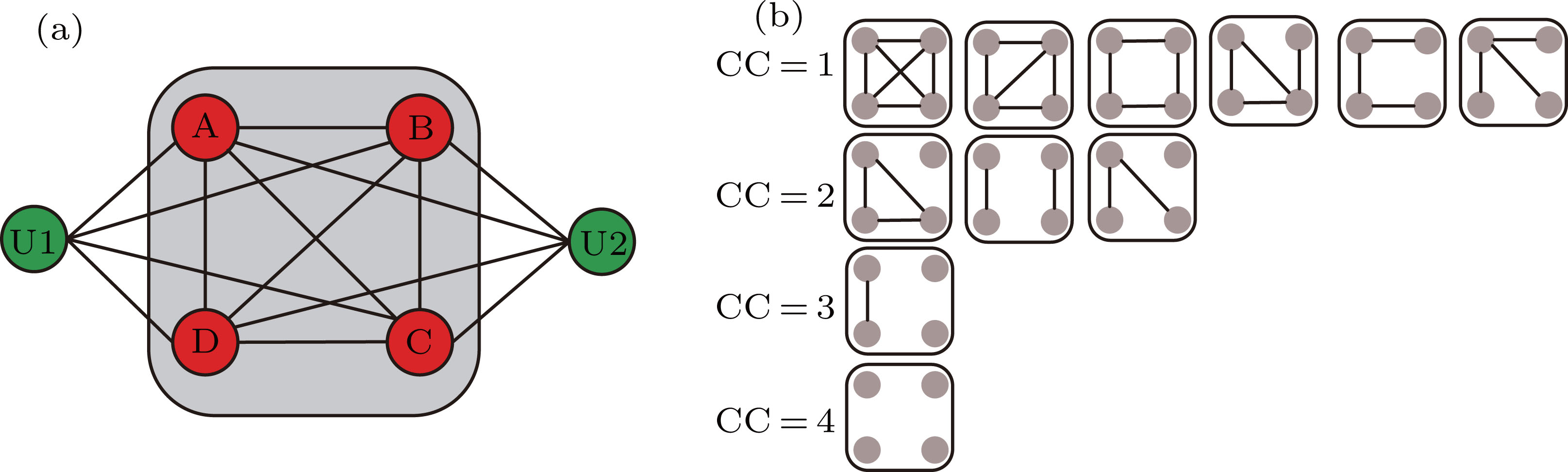
Common Neighbors (CN) index is a common indicator to explore the structural similarity of two users in social networks. The definition of CN is 7 where denotes the set of neighbors of node x. The higher CN is, the more similar two users are.

The other index that can explore the structural diversity is the subgraph structure of common neighbors. We measure this index by the Number of small Connected Components (NCC) in the induced subgraph of common neighbors. For example, in Fig. 11(a) the nodes A, B, C, and D are common neighbors of the nodes U₁ and U₂ and they are wholly connected. Therefore, these four common neighbors are separated into one component. Figure 11(b) shows all of the possible scenarios that four common neighbors may cluster into one, two, three or four connected components with different formations.^[25] A higher NCC indicates more groups and higher structural diversity.^[32]

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. An illustration of the subgraph structures of common neighbors: (a) the topology of two users and their common four neighbors and (b) an illustration of the subgraph structures of four common neighbors.

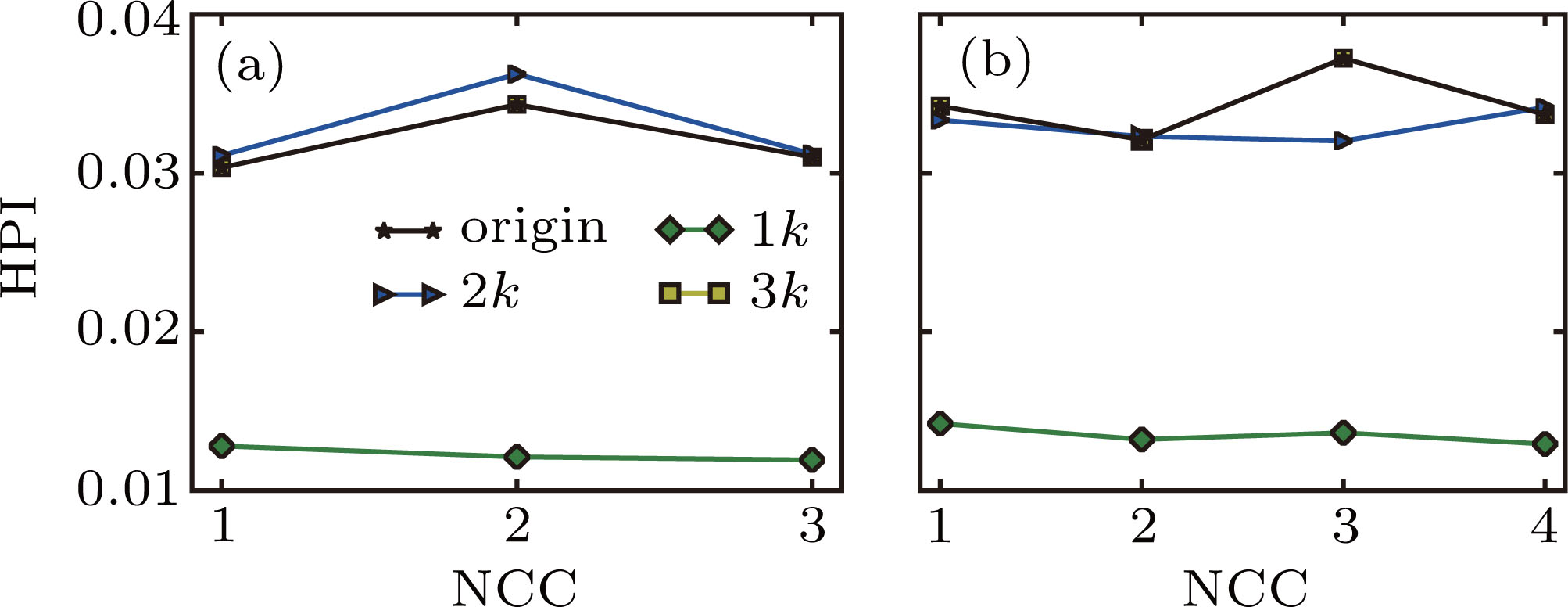
We calculate the number of common neighbors in the original network and its corresponding 1k–3k null networks respectively to study event similarity between friends, and the corresponding HPI results are shown in Fig. 12. Here, simulations have been repeated 100 times independently for null models to achieve the average result. We use different types of lines to represent the original network and its corresponding 1k–3k null networks. The original network and its corresponding null networks show a similar tendency; that is, the HPI values increase gradually as the number of CN increases. In addition, the HPI values of users without common neighbors are less than those with common neighbors. The results indicate that there is a strong correlation between online social proximity and offline event similarity, while the number of CNs has a positive impact on the event similarity between friends.

Fig. 12.

	Figure Option ViewDownloadNew Window
	Fig. 12. The event similarity for different number of common neighbors. The x coordinate represents the CN values, and the y coordinate represents HPI values.

The results in Fig. 12 inspire us to study event similarity from the perspective of the subgraph structure of common neighbors.

In Fig. 13(a), in the case of CN = 3, we calculate the HPI values of different NCC of the original network and its corresponding 1k–3k null networks, and find that not only the original network HPI values but also null models do not show any regularity. It is indicated that the subgraph structure of common neighbors (motif diversity) has no positive impact on offline event similarity. The same method is used to get the results of the case of CN = 4, which is shown in Fig. 13(b). We can gain the same conclusion as the case of CN = 3.

Fig. 13.

	Figure Option ViewDownloadNew Window
	Fig. 13. Event similarity for the different NCC in the induced subgraph of common neighbors: (a) the HPI of NCC of three common neighbors, and (b) the HPI of NCC of four common neighbors. The x coordinate represents the NCC values, and the y coordinate represents HPI values.

Figure 12 and 13 show that the subgraph structure of the CN has no positive impact on offline event similarity while the number of CNs plays a key role. This is different from the results in ^[25]. From our point of view, the reason for this result may be due to social influence.^[31]

The event data bring not only huge benefits to people but also the harm of personal information leakage.^[33] This happens because event data not only directly contains user privacy information but also implies personality habits, health status, social status, and other sensitive information about the users. Once event data are improperly used, all aspects of users’ privacy will be seriously threatened. Actually, the randomness of different null networks corresponds to the degree of information available for privacy protection. We calculate the HPI values of six null models, and the results are shown in Fig. 14. Experimental results show that the HPI values of online null networks are higher than those of offline null networks, indicating that the randomness of online null networks is less than that of offline null models. We also find that the HPI values of online null networks go down as the order decreases, and the randomness of online null networks goes down as the order increases. When the construction method combines online and offline networks, the HPI values are closer to those of the offline. This indicates that the offline characteristic has a greater impact on event similarity than online network structures.

Fig. 14.

Figure Option ViewDownloadNew Window

Fig. 14. The influence degree of online social factors and offline event factors. The x coordinate represents the random method, and the y coordinate represents the HPI values. ET denotes the null networks of exchanging trajectory, and EU represents the null networks of exchanging user events. 0kET represents the null networks combining 0k and exchanging trajectory, and 0kEU represents the null networks combining 0k and exchanging user events.