† Corresponding author. E-mail:
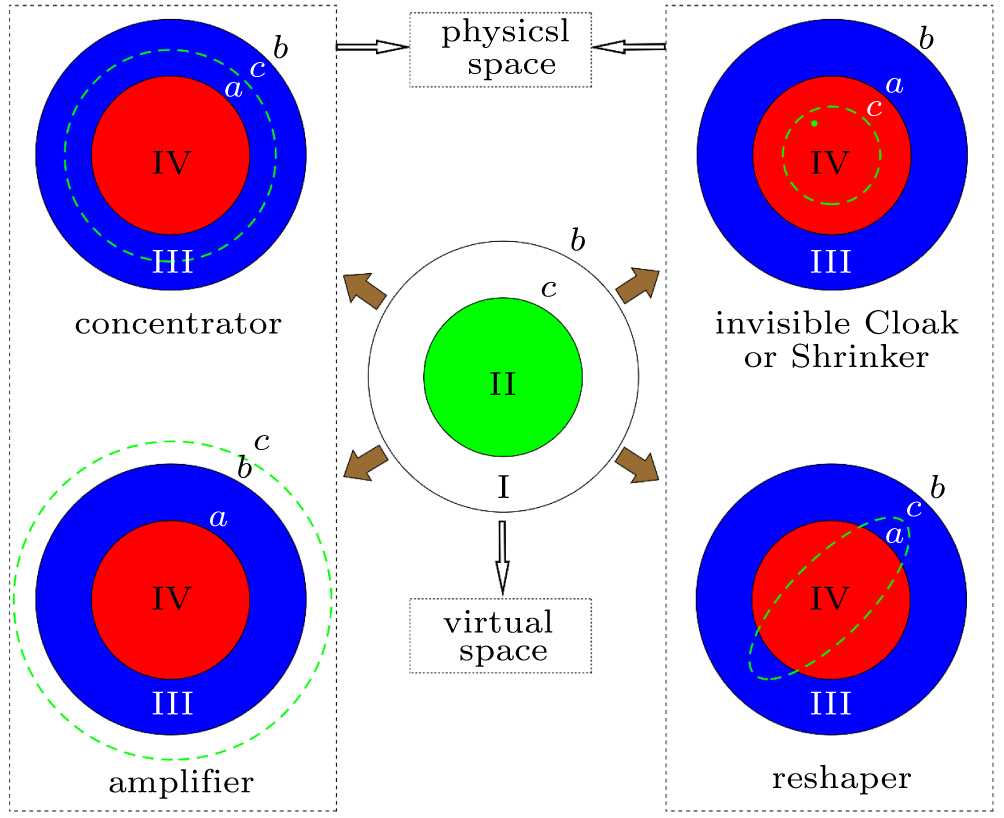
Since the concept of invisible cloak was proposed by Pendry and Leonhardt in 2006, many researchers have applied the theory of coordinate transformation to thermodynamics and overcome the complexity of inhomogeneous and anisotropic of material parameters. However, only two-dimensional (2D) thermal illusion devices are researched recently. According to this situation, our study focuses on three-dimensional (3D) thermal illusion devices including shrinker (or invisible cloak), concentrator, amplifier, reshaper, and rotator with arbitrary shape in a general way. In this paper, the corresponding material parameters of thermal illusion devices mentioned above are derived based on the theory of transformation thermodynamics and the simulated results agree well with the theoretical derivations. In addition, the conventional invisible cloak just controls the temperature gradient rather than the temperature value which is more concerned in physical applications. Here, we find that the temperature value of the cloaked object can be controlled by adjusting the location of the original point of the coordinate system.
Heat energy which is full of mystery attracts researchers to explore the method of manipulating heat flux. According to the second law of thermodynamics, heat always flows from the hotter body to the colder one, which results in colossal difficulties for us to control heat flux. The hope is rooted in the concept of coordinate transformation that Pendry proposed in 2006 to design a device which makes object invisible towards electromagnetic waves.[1] The form-invariance of the corresponding physical equations[2,3] becomes the basic condition of coordinate transformation. Fortunately, many control equations have been proved to be form-invariant, which makes it possible to introduce coordinate transformation into other physical fields, such as microwave,[4] acoustics,[5,6] elastic waves,[7] mater waves,[8] and heat flux,[9] to design corresponding metastructures with fantastic functionalities. Based on the previous study, experts began to design thermal metastructures to control heat transfer in 2008. References [10] and [11] firstly proposed the idea of thermal invisible cloak and constructed the theory of transformation thermotics in steady state. With time passing by, Guenneau et al.[12] extended transformation thermotics from steady state to transient state in 2012 (named transformation thermodynamics), which made scientific community put more and more attention into the interesting issue. From then on, a series of novel thermal devices have been theoretically designed and experimentally realized,[13–31] such as thermal cloaks and thermal camouflages,[20,21] thermal concentrators,[9,18] thermal rotators,[9] and macroscopic thermal diodes,[15] etc., which open a fascinating door to control heat flux efficiently. In the process of fabricating metastructures, a sequence of approaches have been proposed to eliminate the inhomogeneity and singularities of the materials, including multilayered thermal devices based on effective medium theory[14,28] and a bilayer thermal cloak[13] based on scattering cancellation (or neutral inclusion theory.[20,22]) Meanwhile, a series of novel thermal illusion devices have been proposed in recent years. Reference [21] designed a thermal illusion device which could transform the thermal scattering signature of an arbitrary object to multiple isolated objects, and reference [32] realized a thermal illusion device which could transform a good thermal conductor to a poor one through the method of separation variables. References [33] and [34] designed thermal illusion devices based on the equation of heat conduction. At the process of designing thermal illusion devices, the method of coordinate transformation has played an important role. Based on coordinate transformation, references [35]–[38] reported a series of thermal illusion devices which could change the signature of heat source, including the position, the shape, or the quantity of heat source. Reference [27] designed a structure based on transformation thermotics which aimed at thermal radiation and was applicable to complex unknown environments.
However, the preceding studies mainly concentrate on the research of two-dimensional (2D) thermal illusion devices with arbitrary shape[30] and seldom discuss three-dimensional (3D) cases except Ref. [29] (a spherical thermal cloak was proposed). It is necessary to extend thermal illusion devices from 2D to 3D random shape for the practical application of thermal metastructures. Therefore, this paper gives a general method to design 3D thermal illusion devices based on coordinate transformation, including thermal shrinker (or invisible cloak), concentrator, amplifier, reshaper and rotator theoretically and verifies the theoretical derivations through simulations.
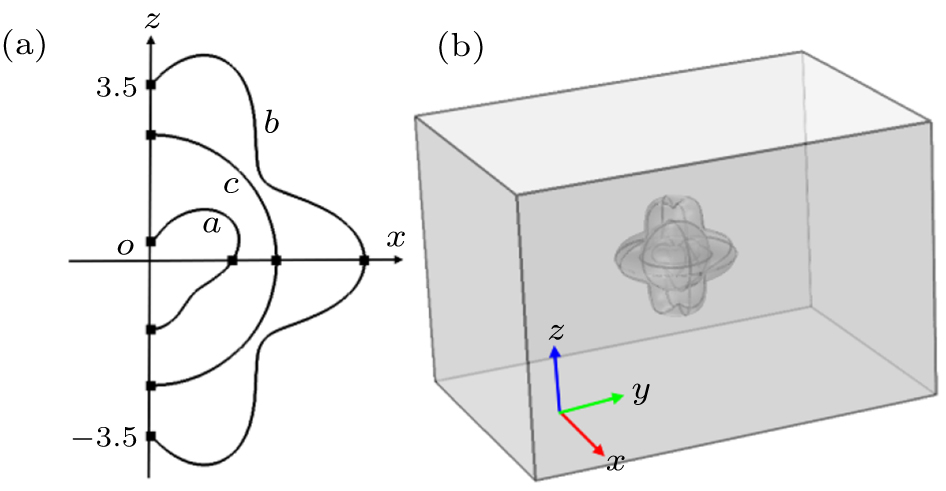
To construct the model of 3D thermal illusion devices with arbitrary shape in spherical coordinate, the inner and outer boundaries of the thermal illusion devices can be parameterized by varying radii[31]
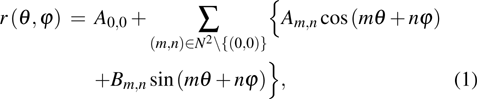 |
According to Fourierʼs law, the heat conduction equation without heat source is described by
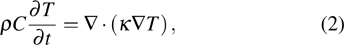 |
A series of thermal devices can be designed through transforming 
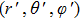
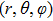

In Fig. 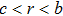
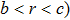
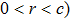
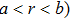
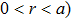
Keeping θ and φ invariant and transforming r to 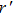
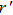
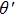
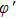
 |
 |
According to Eqs. (
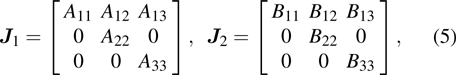 |
 |
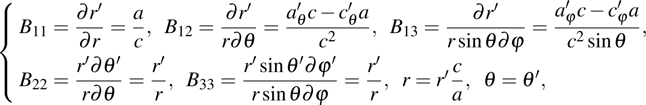 |
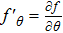
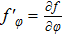
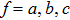
According to Ref. [31] and Eq. (
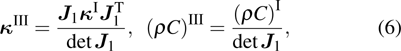 |
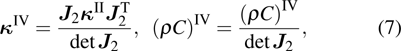 |
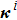
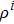
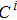
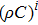
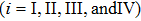
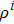
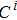
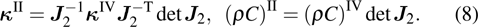 |
Equations (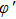
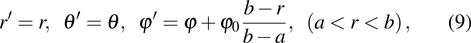 |
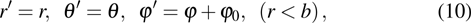 |
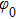
For facility of simulations based on the finite element method, the material parameters in the Cartesian coordinate system are derived by the following Jacobian matrix:
 |
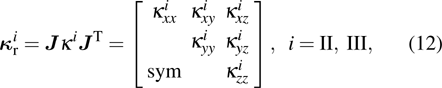 |
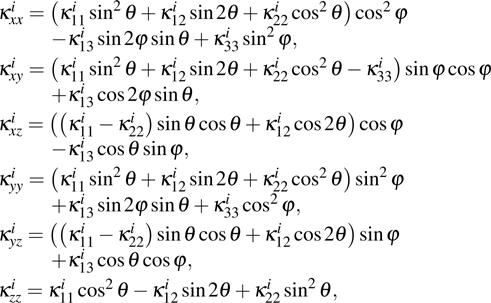 |
Since the necessary material parameters for designing the thermal illusion devices have been given above, the simulations conducted in the finite element software COMSOL Multiphysics will be introduced hereafter to display and verify the theoretical results mentioned above. To decrease the load of calculation and without loss of generality, it is enough to analyze arbitrary thermal illusion devices built with surfaces of revolution, i.e., generated by rotating a curve about the z-axis. In this paper, we discuss the design of axially invariant 3D devices with an arbitrary cross-section described by variable radii r(θ) that gives an angle dependent distance from the origin. According to Eq. (
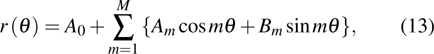 |
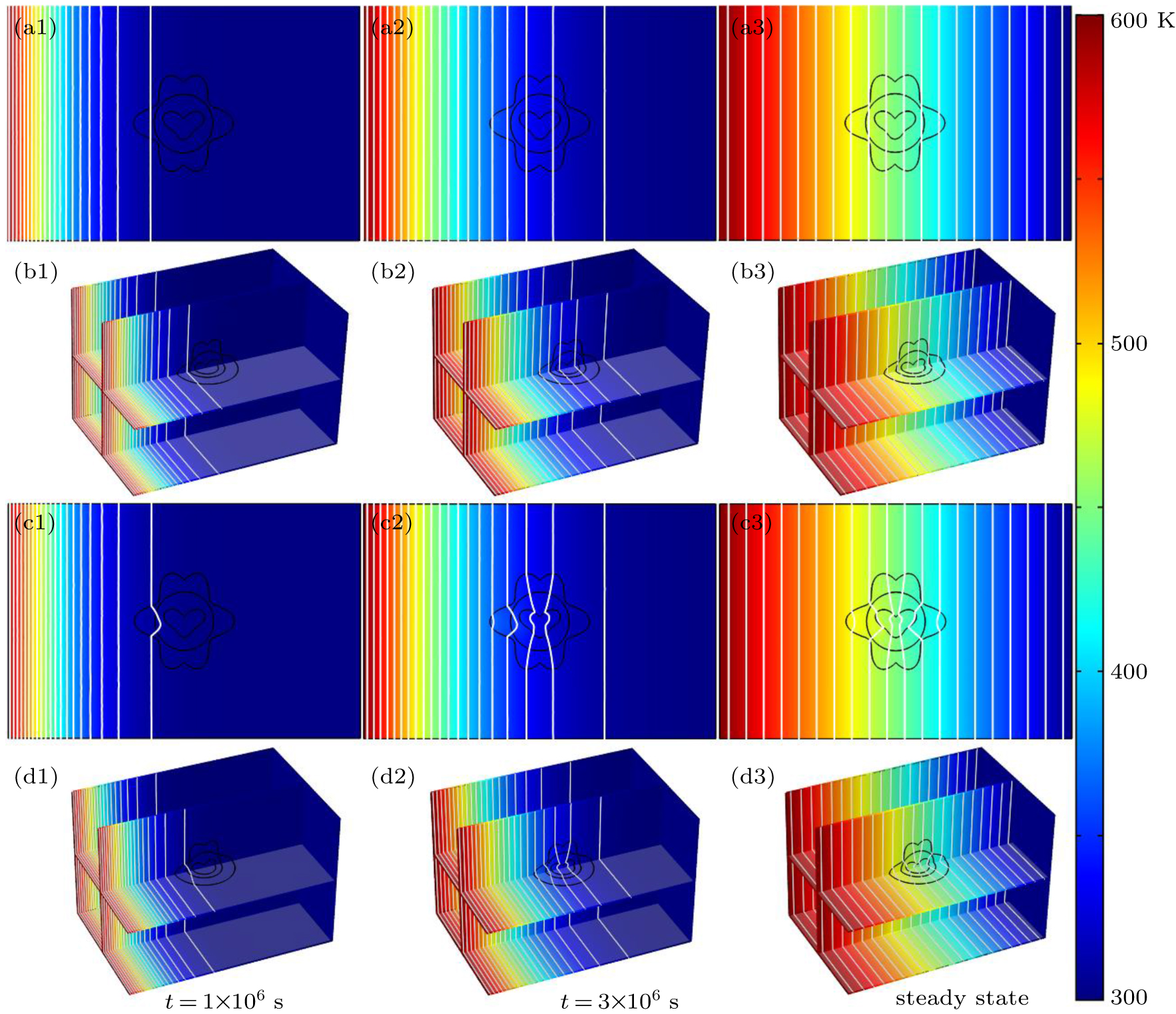
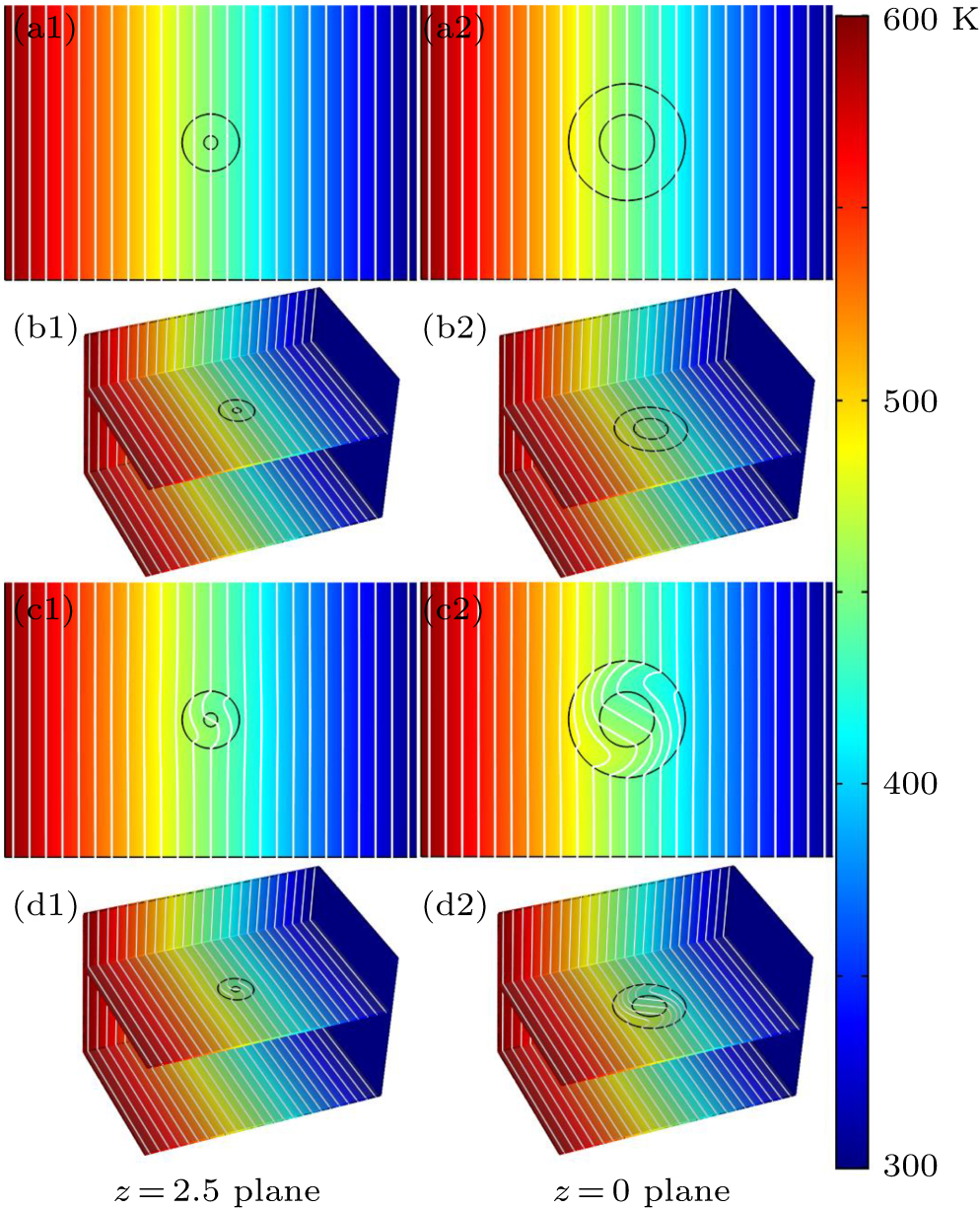
In the process of simulation, the background region is a cuboid, the left and right boundary conditions of the cuboid are 600 K and 300 K, respectively, the other boundary conditions are insulation, and the isothermal lines are denoted by the white lines in the simulation results. For the cases of thermal invisible cloak, concentrator, and rotator, the parameters have been set as 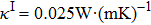
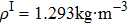
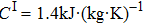
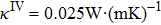
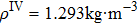
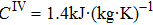
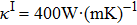
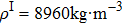
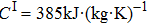
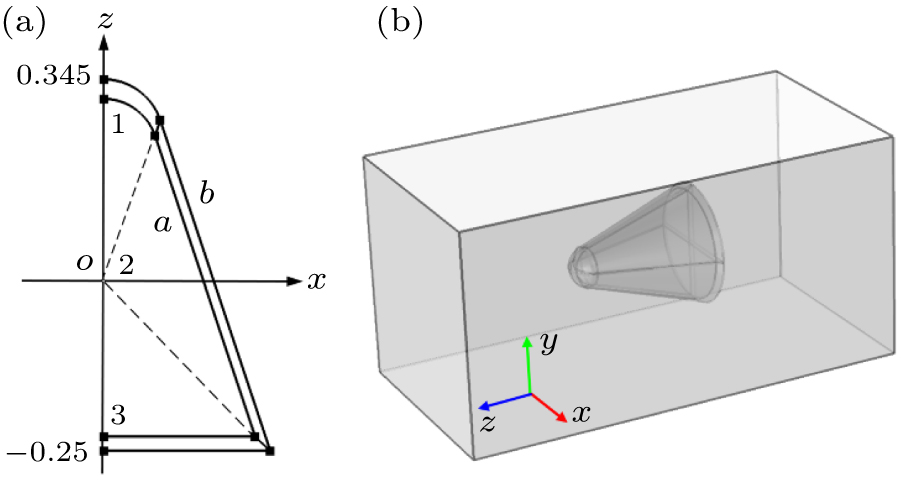
The shape of the simulated thermal invisible cloak is displayed in Fig.
Without loss of generality, a rotational solid similar to the top of a missile has been embedded into an isotropic homogeneous cuboid background material. Parameters of the cloak (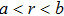
In addition, another interesting phenomenon shows that the temperature of the cloaked object will vary with the location of the original point of the coordinate system and the temperature value in the core is equal to the temperature value in the z = 0 plane. In order to explore the problem of controlling the temperature value rather than the thermal gradient, the location of the original point in Fig.
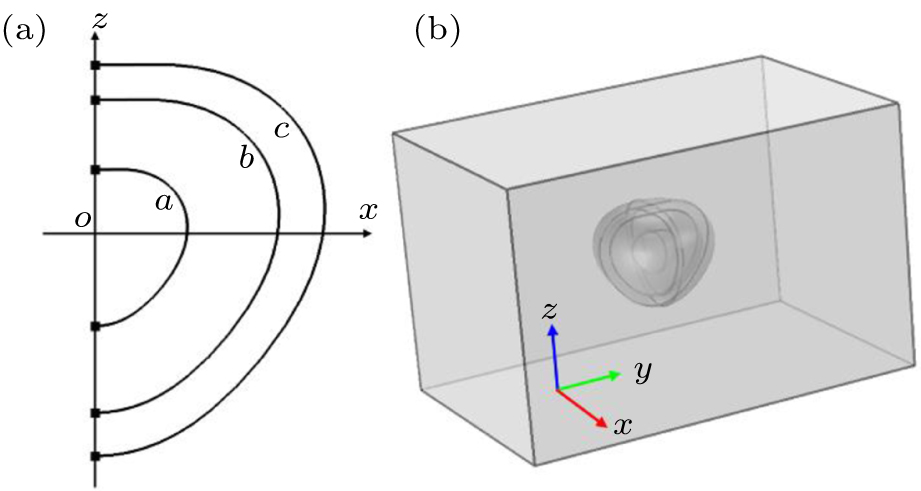
To further demonstrate the validity and generality of the derivations in this paper, the simulation of a thermal concentrator (with boundaries a, b, and c) has been carried out as well. The simulated configuration and results of the thermal concentrator are illustrated in Figs. 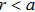

 | Fig. 5. The simulated configuration of a concentrator. Panel (a) is the basic profile of the concentrator. Panel (b) is the schematic illustration of the simulated sample. |
Meanwhile, a thermal amplifier has been constructed by the same method. The basic simulation model and results are illustrated in Figs. 

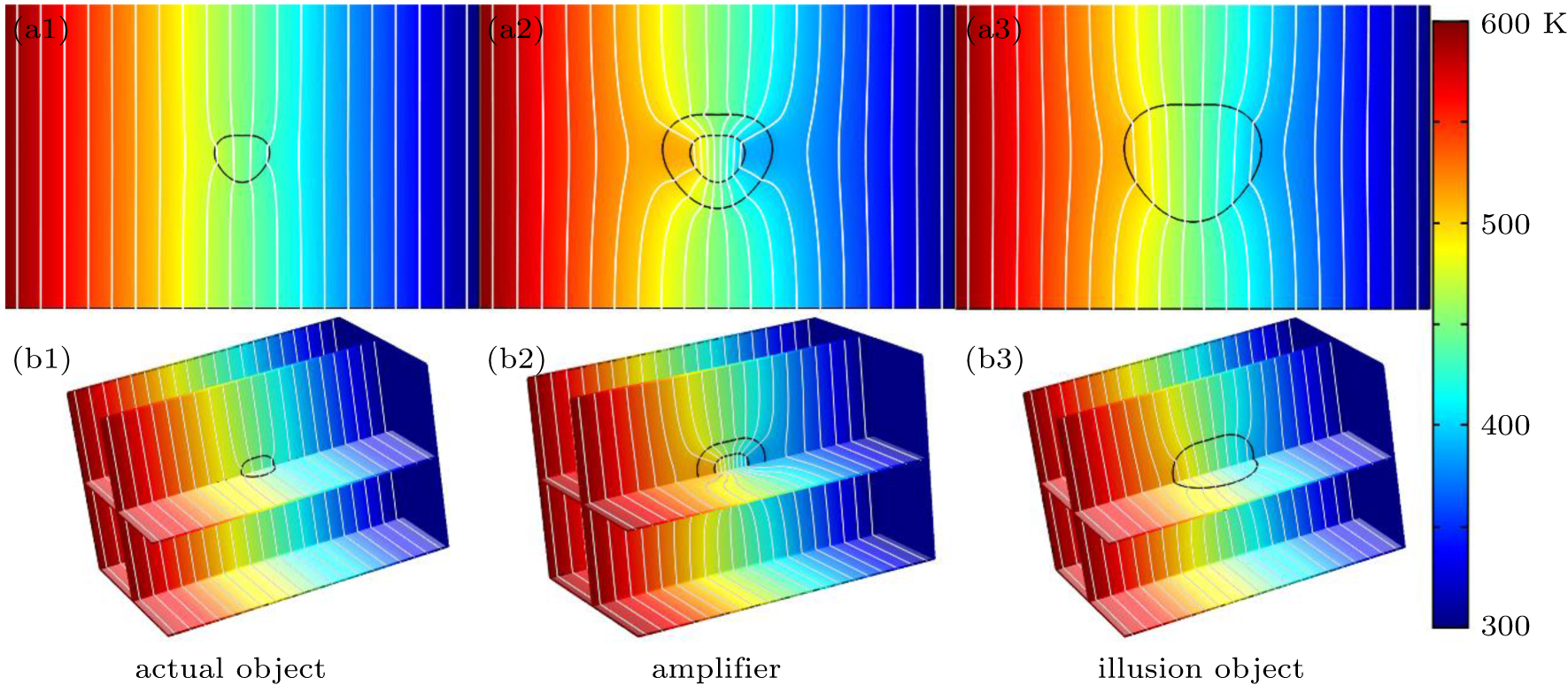 | Fig. 8. The simulation results of a thermal amplifier. Panels (a1)–(a3) are the 2D simulation results in the yz plane (x = 0), and panels (b1)–(b3) are the 3D simulation results. |
Furthermore, a thermal reshaper constructed by Eqs. (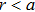
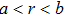
 | Fig. 9. The simulated configuration of a reshaper. Panel (a) is the basic profile of the cross section of the reshaper. Panel (b) is the reshaper that has been placed into a cuboid. |
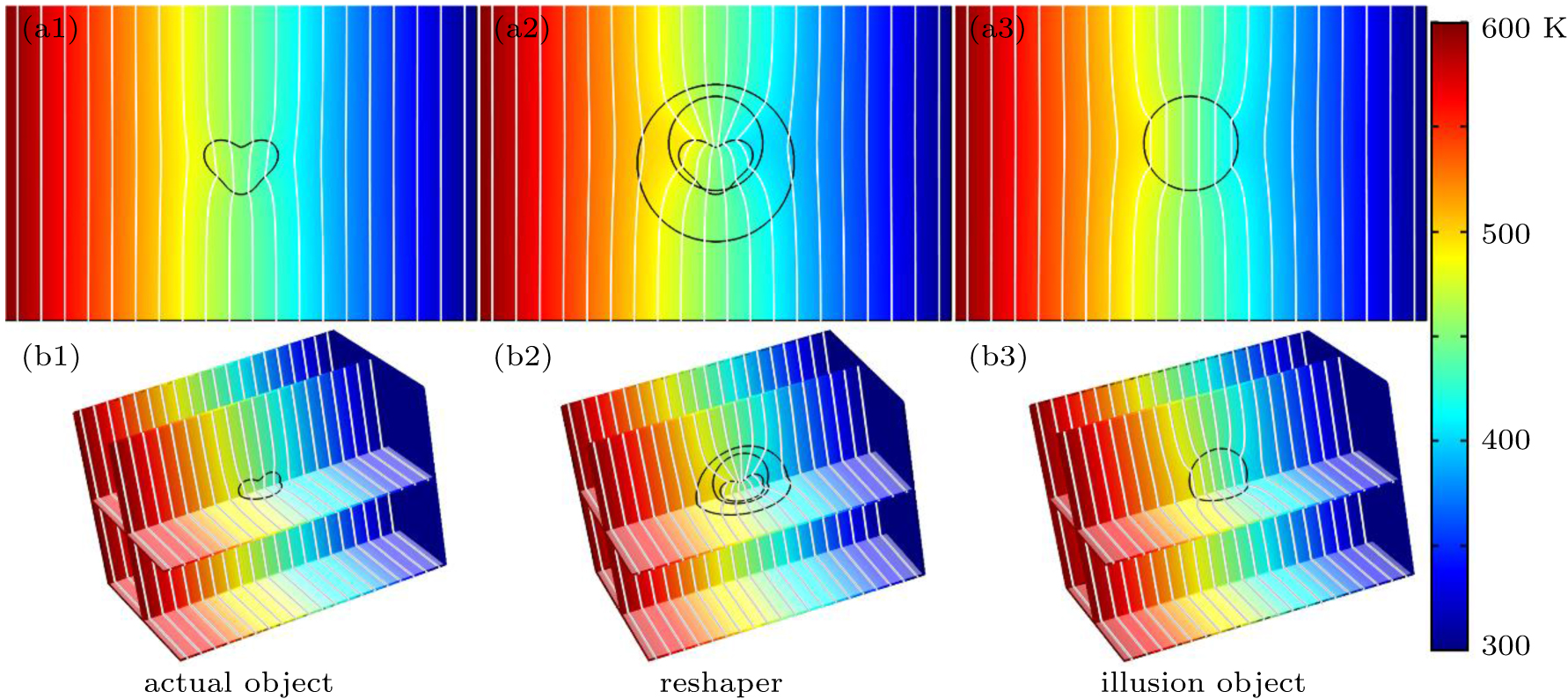 | Fig. 10. The simulation results of thermal reshaper. Panels (a1)–(a3) and (b1)–(b3) are the 2D and 3D simulation results in the xz plane (y = 0), respectively. |
At last, a thermal rotator (with boundaries a and b) can be designed by the general method mentioned above through the transformation Eqs. (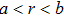

 | Fig. 11. The simulated configuration of a rotator. Panel (a) is the basic profile of the cross section of the rotator. Panel (b) is the schematic illustration of the simulated sample. |
This paper proposes a general way to fabricate 3D thermal illusion devices with arbitrary cross section including thermal shrinker (or invisible cloak), concentrator, amplifier, reshaper, and rotator based on the theory of transformation thermodynamics. All the thermal illusion devices motioned above have been successfully simulated to verify the validity and efficiency of the theoretical derivations by finite element method. Simultaneously, the influence of the location of the coordinate origin on the temperature value of the cloaked object has been discussed. It is found that the temperature value of the cloaked object can be manipulated by adjusting the location of the origin point, and this phenomenon should be used to design the metamaterials with the function of guiding heat flux from higher temperature (or lower temperature) to lower temperature (or higher temperature) autonomously without forcing energy source on the cloak. This phenomenon is not only limited to the thermodynamics, but also it can be generalized into other physical fields, which can be used to control the internal signal rather than eliminating the external disturbance only.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] |