† Corresponding author. E-mail:
The uniformity principle of temperature difference field is very useful in heat exchanger analyses and optimizations. In this paper, we analyze some other heat transfer optimization problems in the thermal management system of spacecrafts, including the cooling of thermal components, the one-stream series-wound heat exchanger network, the volume-to-point heat conduction problem, and the radiative heat transfer optimization problem, and have found that the uniformity principle of temperature difference field also holds. When the design objectives under the given constraints are achieved, the distributions of the temperature difference fields are uniform. The principle reflects the characteristic of the distribution of potential in the heat transfer optimization problems. It is also shown that the principle is consistent with the entransy theory. Therefore, although the principle is intuitive and phenomenological, the entransy theory can be the physical basis of the principle.
Heat exchangers are very important and widely used in thermal engineering. For the analyses and design of heat exchangers, Guo et al.[1,2] proposed a parameter, the uniformity factor of temperature difference field. For a two-stream heat exchanger, its definition is[1–3]



The principle finds many applications in engineering because it is very convenient for designing and optimizing heat exchangers. For instance, if some local temperature differences in one heat exchanger are obviously higher than other places, the principle tells us that our technical design should decrease the local temperature differences to increase the heat exchanger effectiveness. However, it should be pointed out that the principle is not from the viewpoint of the irreversibility of heat transfer, but is intuitive and phenomenological. Therefore, the physical basis of the principle should be investigated. In the entransy theory,[9] it has been proved that the concept of entransy dissipation can describe the irreversibility of heat transfer.[10,11] With this theory, Song et al.[6] analyzed one-dimensional two-stream and three-stream heat exchangers and proved that the principle holds when the heat transfer rate or the entransy dissipation rate is fixed. In the analyses of two-stream heat exchangers, Cheng et al.[4] set up the mathematical relationship between the uniformity factor of temperature difference field and the heat exchanger effectiveness with the help of the entransy theory, and found that larger uniformity factor of temperature difference field always corresponds to smaller entransy-dissipation-based thermal resistance. Therefore, larger uniformity factor of temperature difference field means better heat transfer, and the entransy theory can be the physical basis of the intuitive and phenomenological principle.
Furthermore, it is obvious that the application scope of the principle is limited because it can only be used to analyze and optimize heat exchangers. In this paper, we try to extend the application scope of the principle, and analyze the applicability of the principle to the heat transfer processes in the thermal management system of spacecrafts. The cooling problem of thermal components, the one-stream heat exchanger networks, the volume-to-point heat conduction optimization for cooling electronic devices, and the radiative heat transfer optimization are analyzed. The physical basis of the principle in the new application cases is also discussed.
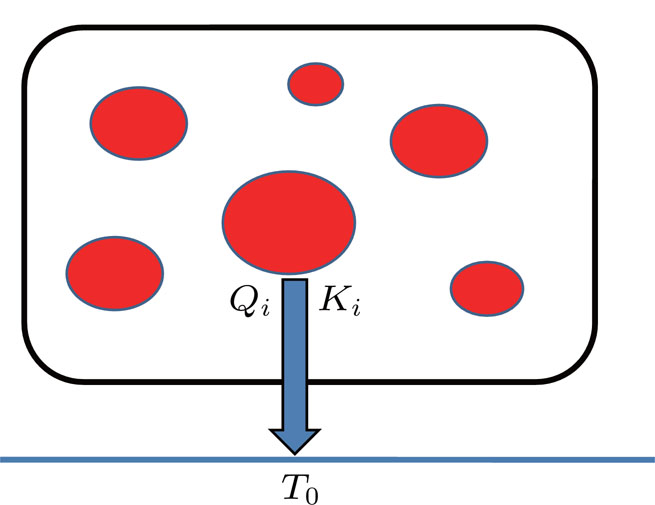
In the thermal management system of spacecrafts, the cooling of thermal components may be simplified to the steady heat transfer system shown in Fig.

With Eq. (
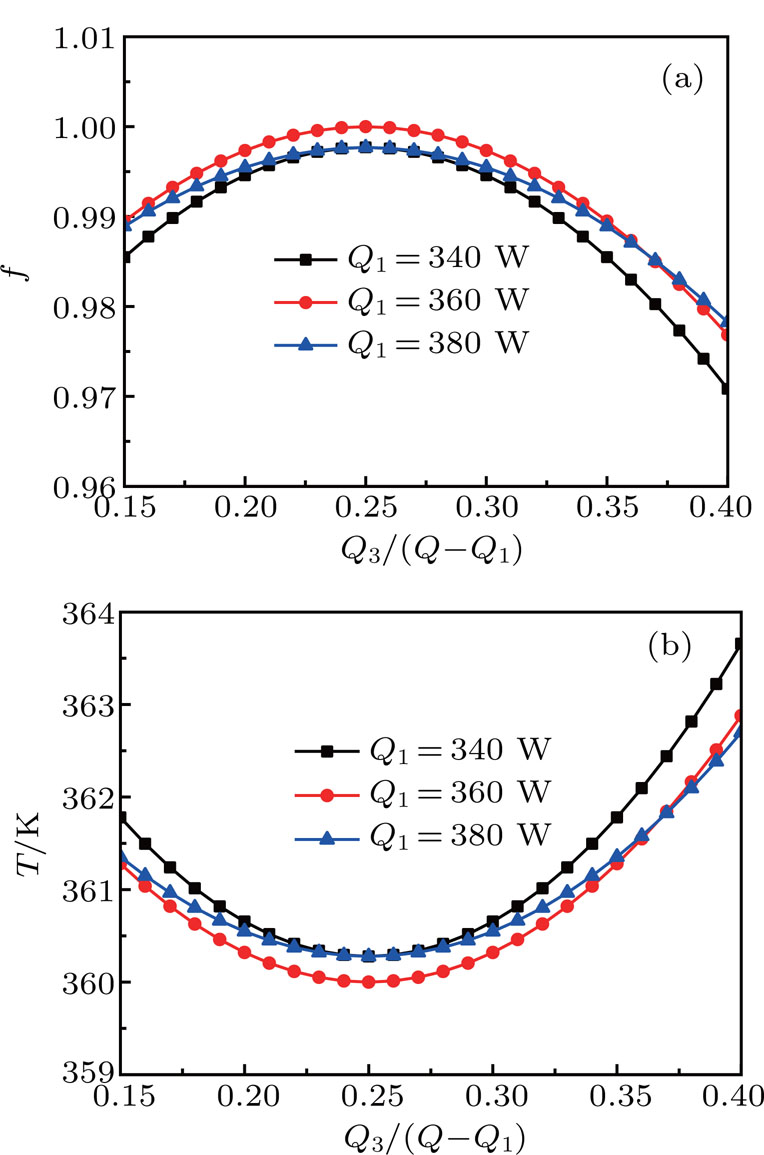
As below, a numerical example is presented. Assume that there are three thermal components in the system, the heat transfer rates Q1 = 300 W, Q2 = 150 W, and Q3 = 50 W, the total thermal conductance K = 20 W/K and the temperature T0 = 300 K. For the system, the uniformity factor of temperature difference field can be defined as
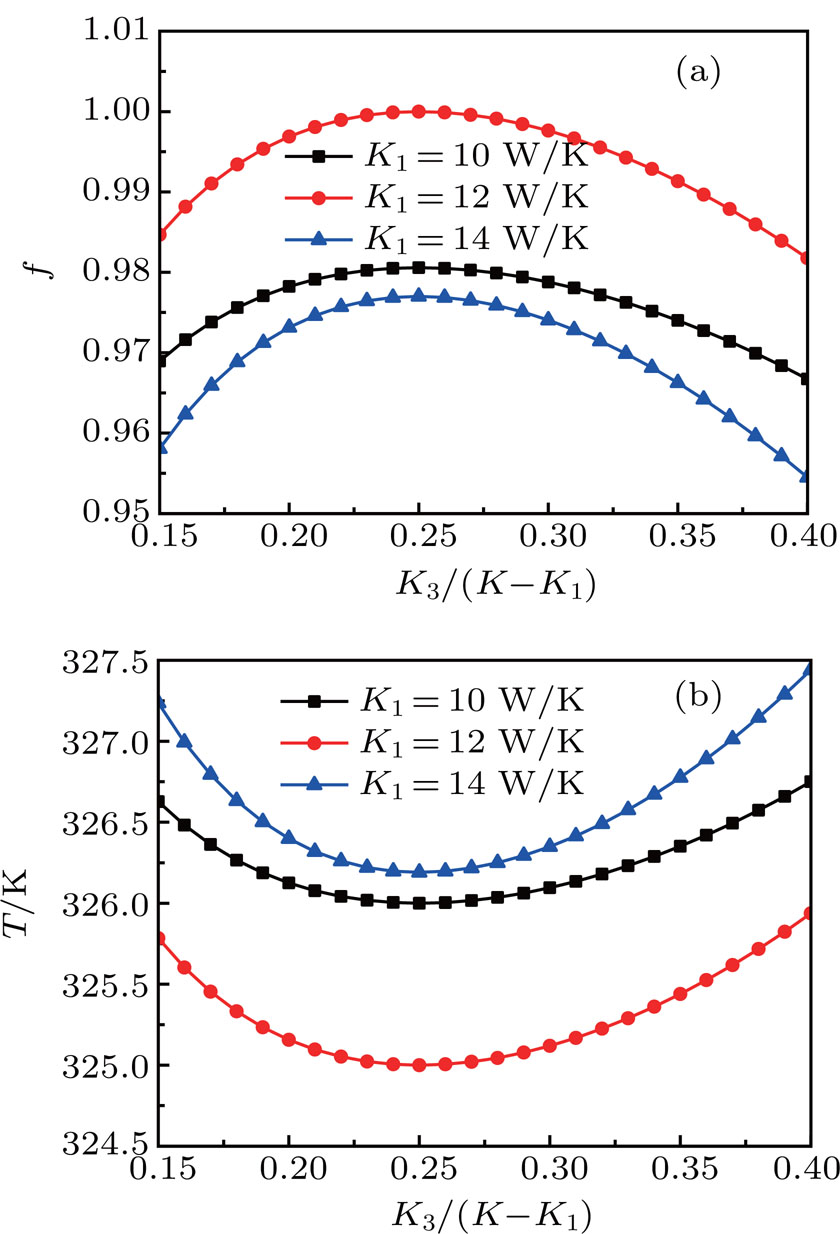
Second, we can assume that the thermal conductance of each thermal component is given, and the limiting condition is

With Eq. (
As below, a numerical example can also be presented. We can also assume that there are three thermal components, the thermal conductance K1 = 6 W/K, K2 = 3 W/K, and K3 = 1 W/K, the total heat transfer rate Q = 600 W, and the temperature T0 = 300 K. In this case, the variations of the average temperature of the thermal components weighted by released heat flow rate and the uniformity factor of temperature difference field with the distribution of the total released heat flow rate are calculated and shown in Fig.
It can be seen that the theoretical and numerical optimization results of the cases above all lead to uniform heat transfer temperature difference fields. Therefore, the uniformity principle of temperature difference field holds in these heat transfer optimization problems.
Heat exchanger networks are widely used in the thermal management system of spacecrafts. As shown in Fig.
 | Fig. 4. A one-stream series-wound heat exchanger network.[13] |
For the i-th thermal component, we can assume that[12,13]

Based on the entransy theory,[9] we have proved that the minimization of Eq. (

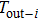

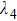
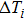
Here, a numerical example can also be presented. Assume that there are three thermal components, the heat capacity flow rate cm = 100 W/K, the heat transfer coefficient k, the mass flow rate m and the heat capacity c satisfy 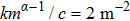
In the thermal management system of spacecrafts, there are many electronic devices that should be cooled, and the cooling problem may be simplified to be the volume-to-point heat conduction problem. As shown in Fig.
The limiting condition of the problem is
With the entransy theory,[9] we can find that the entransy balance of the system is
In heat conduction, the entransy dissipation rate can be expressed as[9,14]
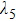
The optimization analyses of radiative heat transfer processes also widely exist in the thermal management system of spacecrafts. Assume that there are n thermal components on a flat plate, and the thermal components release heat flow into the environment at temperature T0 only through radiative heat transfer. For the i-th thermal component, the temperature is Ti, the released heat flow rate is Qi, the heat transfer area is Ai, and the thermal emissivity is 
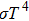
First, we assume that the limiting condition is


Furthermore, we can analyze a case in which the values of Ei are fixed, and the limiting condition is expressed by Eq. (

For the two optimization problems discussed above, it can be seen that the mathematical expressions are very similar to those in Section
From the analyses above, it can be seen that the derivations are related to the entransy theory. As below, the consistence between the uniformity principle of temperature difference field and the entransy theory is analyzed and discussed.
In the analyses of one-dimensional two-stream and three-stream heat exchangers, Song et al.[6] proved that a uniform temperature difference field would lead to the maximum heat transfer rate with the prescribed entransy dissipation rate and the minimum entransy dissipation rate with the prescribed heat transfer rate, respectively. For two-stream heat exchangers, Cheng et al.[4] proved that
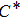
In the analyses from Section
For the system shown in Fig.
It is clear that the uniformity principle of temperature difference field works for the application cases in the thermal management system of spacecrafts in this paper, and a more uniform temperature difference field leads to better heat transfer. The principle is also very intuitive and phenomenological. Therefore, in the design of the thermal management system in spacecrafts, if we find that the temperature difference field is not uniform, we can intuitively conclude that the heat transfer is not optimal, and then we can change the relevant parameters to increase the uniformity of the temperature difference field. Correspondingly, the heat transfer performance of the system can be improved. Hence, the uniformity principle of temperature difference field can be very useful in engineering. Furthermore, as the principle is consistent with the entransy theory, which profoundly reveals the physical nature of heat transfer and is widely used in many thermal systems,[9–43] the entransy theory can work as the physical basis of the principle and provide the corresponding explanations of the physical mechanisms.
In nature, flows are driven by the corresponding potentials. For instance, the potentials of fluid flow, electrical current, conductive heat transfer, and radiative heat transfer are pressure, voltage, temperature, and radiative thermal potential, respectively. In the optimizations of these flows, the distributions of the corresponding potentials are also adjusted to achieve the optimization objectives. As below, the uniformity principle of temperature difference field in heat transfer optimization is discussed from this viewpoint.
From a certain point of view, we can say that a heat transfer system is composed of many subsystems which are located at different positions of the whole system. With specific constraints, the change of the heat transfer process in any subsystem can not only affect the heat transfer performance of the heat transfer process itself, but also affect the performance of the whole system. Therefore, the heat transfer optimization under given constraints and objectives can be treated as a result of competing and balancing the heat transfer processes of the subsystems. At the same time, the competition and balance of the heat transfer processes in the subsystems can obviously lead to the change of the distribution of the driving potential. Here, the uniformity principle of temperature difference field just reflects the equipartition of potential in heat transfer.
In two-stream heat exchangers, if the heat exchanger is divided into many parts along the direction of fluid flow, it can be seen that the heat transfer processes of the parts are connected in series, and the heat flows are transferred into the fluid at different potentials. In this case, the competing and balancing of the heat transfer processes lead to a uniform potential difference field. In the one-stream series-wound heat exchanger network, the thermal components are also connected in series, and the results also show that the potential differences are uniform.
On the other hand, in the systems analyzed in sections
For the i-th thermal component, there is
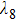


In heat transfer optimization, when the constraints, the objectives, or the analyzed system change, maybe the distribution of potential can show some other characteristics, and the uniformity principle of temperature difference field may not hold any more. We should not assume that any theory is omnipotent and always correct.[38] However, when we pay attention to the distribution of potential with the consideration of the competing and balancing of the local heat transfer processes in the subsystems, the uniformity principle of temperature difference field can be obtained in some cases. This is still important and interesting. It is advised that we can analyze the characteristics of the distribution of potential in other heat transfer optimization problems.
In this paper, it is found that the uniformity principle of temperature difference field holds not only for heat exchanger optimization, but also for some other heat transfer optimization problems in the thermal management system of spacecrafts, including the cooling of thermal components, the optimization of a one-stream series-wound heat exchanger network, the volume-to-point heat conduction optimization problem, and the radiative heat transfer optimization. Numerical examples are also presented, and the results have verified the theoretical analyses.
The uniformity principle of temperature difference field is intuitive and phenomenological, and reflects the characteristic of the distribution of potential in the heat transfer optimization cases with specific constraints and design objectives. However, it is shown that the uniformity principle of temperature difference field is consistent with the entransy theory. Therefore, the entransy theory can work as the physical basis of the principle and provide the corresponding explanations of the physical mechanisms.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] |