† Corresponding author. E-mail:
A comprehensive study on the requirements for the highly efficient third harmonic generation (THG) and its inverse process, one-third harmonic generation (OTHG), in lossy waveguides is proposed. The field intensity restrictions for both THG and OTHG caused by loss are demonstrated. The effective relative phase ranges, supporting the positive growth of signal fields of THG and OTHG are shrunken by the loss. Furthermore, it turns out that the effective relative phase ranges depend on the intensities of the interacting fields. At last, a modified definition of coherent length in loss situation, which evaluates the phase matching degree more precisely, is proposed by incorporating the shrunken relative phase range and the nonlinear phase mismatch. These theoretical analysis are valuable for guiding the experimental designs for highly efficient THG and OTHG.
Nonlinear optical processes in optical microfibers have attracted significant interest because of the unique environment, including a tight confinement of light, long interaction lengths, and large manageable waveguide dispersion.[1–3] With a relatively low optical power, many enhanced nonlinear effects, such as supercontinuum generation,[4,5] bistability,[6,7] two-photon absorption,[8,9] third-harmonic generation,[10–13] and one-third harmonic generation,[13–17] have been demonstrated.
In this work, we focus on third-harmonic generation (THG) and one-third harmonic generation (OTHG) in optical microfibers, which are a pair of inverse processes and share the same phase matching condition that can be realized by engineering the waveguide dispersion in optical microfibers. The THG is widely used to produce novel wavelengths, which are attractive to optical logic unit,[18] material processing,[19] and so on. The OTHG, on the other hand, is a potential way to generate the triple photon states with possible applications in quantum cryptography, quantum information processing, and general experiments investigating the fundamental nature of quantum entanglement. The theoretical framework behind THG and OTHG in optical microfibers was developed initially by Grubsky and Savchenko in 2005.[10] Following, laser power and waveguide design parameters for high THG and OTHG efficiency were analyzed with the lossless approximation.[13,15] However, the optical attenuation is unneglectable and influences the nonlinear conversion in real experiments. Several theoretical researches on THG[20–22] and OTHG[14,17,20] have included the optical losses in their numerical calculations, but mainly aim at improving the corresponding conversion efficiency by designing the waveguide parameters. The influences of losses on the optical parameters, including power and phases, have not been systematically investigated for both THG and OTHG processes in microfibers.
Here, a general analysis on THG and OTHG in lossy waveguides is made to get a guideline for the experimental designs to achieve the high efficiencies. The required optical field conditions for THG and OTHG conversions in loss waveguides are deduced from the coupled mode equations. The requirements are quite different from those in the lossless situation. Accordingly, a modified definition of coherent length is proposed to evaluate the phase matching degree in loss situation more precisely. At last, some suggestions for improving the conversion efficiencies of THG and OTHG in lossy waveguides are made based on the analysis.
The fields at 



The coefficients J1, J2, J3, and J5 are the modal overlap integrals, which respectively correspond to the self-phase modulation (SPM) of field at 

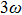





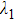



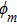

Equations (


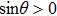
As mentioned above, the field at 

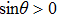

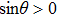
Equation (
With the optimal relative phase value, equation (
This expression indicates that the efficient THG conversion needs the signal field to be lower than a maximum amplitude, which is directly proportional to the material nonlinearity 

If the signal field just results from the THG conversion, rather than from the initial field, there is a maximum limit for the corresponding conversion efficiency with the definition of 

Even though the interacting fields satisfy the amplitude condition of Eq. (

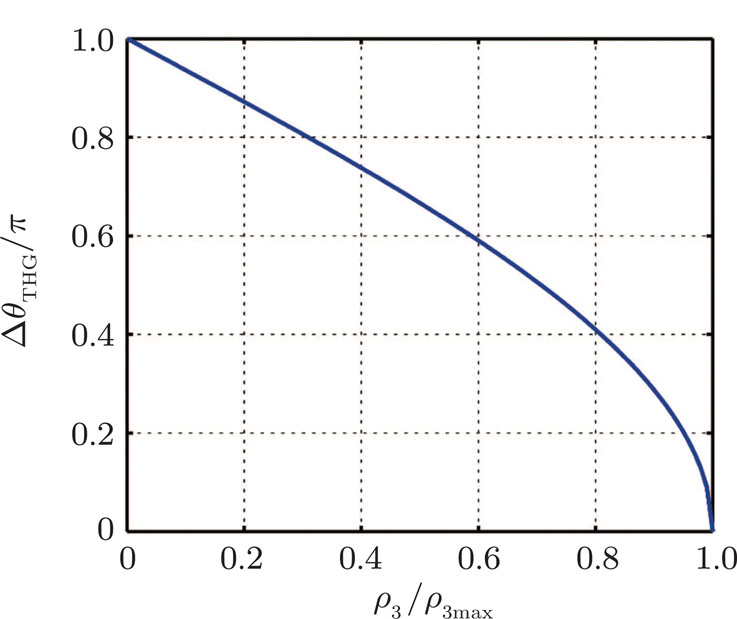 | Fig. 1. Dependence of effective relative phase range of the THG process on the normalized signal amplitude. |
For any given signal maximum amplitude, the effective phase range decreases with the increase of the signal amplitude. On the other hand, the effective phase range increases with the increase of signal maximum amplitude that is proportional to the third power of pump field amplitude, for any given signal amplitude. Thus, the effective phase range can be controlled by adjusting the intensities of the interacting fields.
The OTHG signal field evolution along the propagation path is described by Eq. (



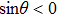
At any location on the propagation path, the effective increase of the OTHG signal field requires the nonlinear transfer term to be larger than the loss term, which can be expressed as:
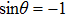

Equation (
The second limit caused by loss effect is the shrinkage of the effective relative phase range. In lossless situation, the relative phase for the OTHG conversion ranges from 

 | Fig. 2. Dependence of effective relative phase range for the OTHG process on the normalized amplitude product. |
The effective relative phase range increases with the increase of the amplitude product larger than threshold, which can be realized by increasing either the pump field or the signal field, or both the two fields. It is different that the increase of the signal amplitude narrows rather than extends the effective range of the relative phase required by efficient THG conversion. The reason of this difference is that the THG is a spontaneous process, while the OTHG is a stimulated process.
The above analysis figures out the requirements of amplitude and relative phase to support the signal positive growth rate of the THG and OTHG processes, respectively. However, it is just one part of what makes for high conversion efficiency. The other part to acquire the efficient gain is a long effective propagation length in which the positive growth rate is maintained, as the final signal increases are the path integral of the amplitude growth rate governed by Eqs. (
Commonly, the effective propagation lengths are mainly restricted by the relative phase variation. It is easy to make the signal field amplitude far below the maximum value for THG process or to make the amplitude product larger than the threshold for OTHG process, while to keep the relative phase within the respective effective ranges are difficult because that the perfect phase matching is critical to be realized. The perfect phase matching can make the relative phase between the two interacting fields as a constant along the propagation path. But this situation occurs only when the modal dispersion fully compensates the nonlinear dispersion caused by optical Kerr effects, as shown by Eq. (
A common parameter to quantitatively describe the phase mismatch is the coherent length, over which the relative phase is kept within the range for THG or OTHG process. In lossless situation, the definition of coherent length is the ratio of the relative phase range 


Consequently, a modified definition of coherent length is proposed as:
As expounded above, the perfect phase matching is hard to be maintained along the propagation path. Therefore, for a given total phase mismatch, the coherent length can be extended by enlarging the effective relative phase ranges. For the THG process, the effective relative phase range can be enlarged by reducing the normalized signal amplitude, as shown by Fig.
In conclusion, we have analyzed the optical field conditions supporting the THG and OTHG signal growth in lossy waveguides. The attenuation sets an upper limit for the THG signal field with the given pump field, and requires the amplitude product of interacting fields of the OTHG process to be larger than a threshold value. With the loss effects considered, the effective relative phase ranges for both THG and OTHG process are related to the strengths of the interacting fields. Based on our analysis, we proposed a modified definition of coherent length and pointed out that the phase matching condition also depends on the strengths of the interacting fields. Even with the severe phase mismatch, the signal increase for THG and OTHG can still be improved by enlarging the effective relative phase ranges. The work presented in this paper can offer a cogent theoretical explanation for the experimental research of THG and OTHG.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] |

