† Corresponding author. E-mail:
The single-pixel imaging (SPI) technique is able to capture two-dimensional (2D) images without conventional array sensors by using a photodiode. As a novel scheme, Fourier single-pixel imaging (FSI) has been proven capable of reconstructing high-quality images. Due to the fact that the Fourier basis patterns (also known as grayscale sinusoidal patterns) cannot be well displayed on the digital micromirror device (DMD), a fast FSI system is proposed to solve this problem by binarizing Fourier pattern through a dithering algorithm. However, the traditional dithering algorithm leads to low quality as the extra noise is inevitably induced in the reconstructed images. In this paper, we report a better dithering algorithm to binarize Fourier pattern, which utilizes the Sierra–Lite kernel function by a serpentine scanning method. Numerical simulation and experiment demonstrate that the proposed algorithm is able to achieve higher quality under different sampling ratios.
In conventional imaging systems, a sensor array is generally required to capture a two-dimensional (2D) image of a scene by collecting light focused through an optical lens. An innovative approach, known as single-pixel imaging (SPI), replaces the multi-pixel sensor with a single photosensitive detector as the imaging device by utilizing a spatial light modulator (SLM) or digital micromirror device (DMD) to provide either time-varying, structured detection of the scene or time-varying, structured illumination onto the scene. The final image is retrieved by correlating the recorded intensity signal with the corresponding structured illumination. The SPI shares the same scheme to ghost imaging (GI),[1–6] and it is often considered to originate from GI.
By capturing 2D images using a single-pixel detector (usually a photodiode), SPI has huge advantages, such as robustness to light scattering, flexible system configuration,[7,8] and low cost, and has been widely applied to three-dimensional (3D) imaging,[9–11] multi-spectral imaging,[12,13] optical encryption, etc. However, low image quality and speed still restrict the development of single-pixel imaging. In recent years, Fourier single-pixel imaging (FSI) technique[12–22] has attracted much attention because it can reconstruct high-quality images by using Fourier basis patterns (also known as grayscale sinusoidal patterns) for illumination. Each four π/2 phase-shifted sinusoidal patterns owning the same single spatial frequency and yielding the scene Fourier coefficient at the spatial spectrum of the scene can be obtained. Then, inverse Fourier transform is applied to reconstruct the scene. Concerning experimental results, this technique has been proven capable of achieving sub-millimetric depth accuracy in multi-modality 3D imaging,[10] imaging,[13] shadow-free imaging,[22] etc. But, from a practical point of view, the grayscale illuminating patterns cannot fully take the advantages of DMD high frame rate binary modulation, which is the key component to achieve the real-time imaging. Therefore, fast FSI system[16] is proposed to solve this problem by using binary Fourier pattern through dithering algorithm, while the dithered pattern would inevitably lead to extra noise in the reconstructed image and the image quality cannot reach the requirement for practical application.
In this paper, the principle of the dithering algorithm is investigated. From the theoretical analysis, we report a better dithering algorithm to binarize Fourier pattern, which utilizes the Sierra–Lite kernel function by a serpentine scanning method. This allows us to achieve higher image quality under the same sampling ratio through the numerical simulation and optical experiment. Consequently, the reported method raises the accuracy of grayscale pattern generation of DMD-based FSI in binary mode and provides an alternative approach to improve FSI image quality.
In contrast from the original single-pixel imaging system directly using binary illuminating patterns, FSI uses Fourier basis patterns for illumination, and each basis pattern 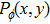
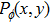
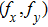
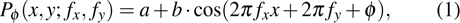 |
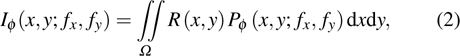 |
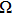
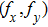
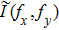
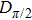
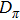
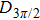
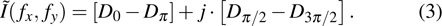 |
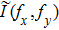
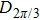
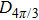
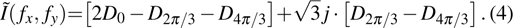 |
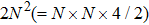
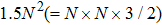
Since most of the illuminating patterns are binary modulated, the original single-pixel imaging system lends itself well to the DMD-based device by using its binary modulation (each DMD mirror has only two states ‘ON’ and ‘OFF’) at its maximum rate (∼22 kHz). However, DMD cannot generate grayscale patterns directly but only displays ∼290 Hz at its 8-bit mode. Therefore, the grayscale FSI is challenging to apply to high-speed real-time imaging by using a digital projector.
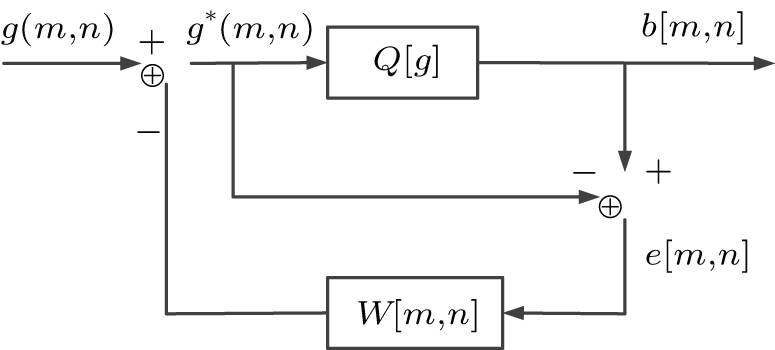
To overcome the weakness for low-rate pattern generation of FSI, Zhang et al.[12] proposed to use a dithering algorithm to convert grayscale sinusoidal patterns to binary sinusoidal patterns based on the idea of error diffusion. The basic idea of the error diffusion method is to compare the current pixel value of the grayscale image with a threshold value to obtain a binary output, and then spread the pixel difference between the input and the output to the several adjacent unprocessed regions by a certain percentage.
The principle of error diffusion can be expressed as
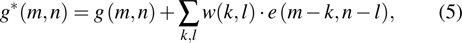 |
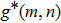
According to the threshold T, the pixel value at 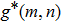
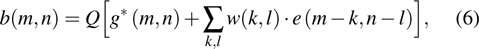 |
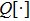
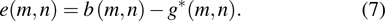 |
To facilitate the analysis of the algorithm, the quantization error e(m,n) can also be written as
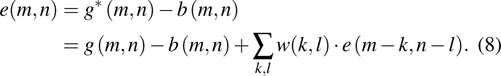 |
The kernel function w(k,l) is the most critical parameter in the error diffusion method and the dithering algorithm will be different with different kernel functions. Usually, the kernel function for traditional dithering algorithm can be expressed as
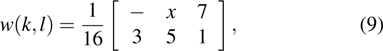 |
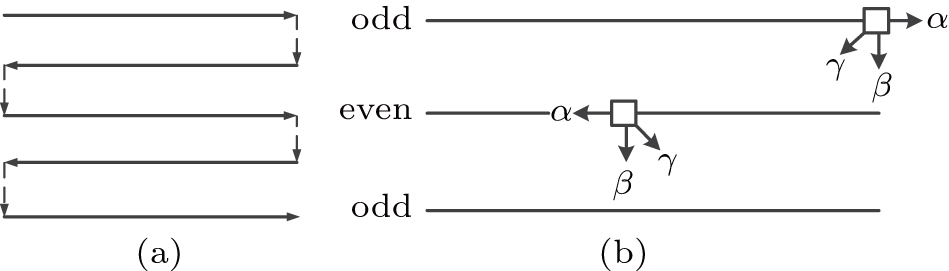
Usually, the traditional algorithm can result in partial structural texture between bright and dark tones, and the boundary processing effect is not ideal in some parts. Simultaneously, the error will cause the water impact of flow and lead to the decrease of the image quality by using sequential scanning method calculating from the left-hand pixel to the right-hand pixel, and then from the top pixel to the bottom pixel. To obtain a smaller quantization error for binary Fourier patterns and better structural similarity with the grayscale Fourier patterns, we report an improved dithering algorithm by utilizing Sierra–Lite kernel function and applying serpentine scanning method; namely, the error is obtained from the left pixel to the right pixel in odd rows, and then from the right pixel to the left pixel in even rows.
Therefore, the kernel function of odd rows can be expressed as
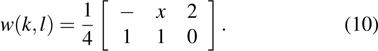 |
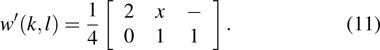 |
The feasibility of the improved dithering algorithm by utilizing the serpentine scanning method is validated by the numerical simulation and optical experiment in the subsection. We use the three-step phase-shifting algorithm, where ϕ is set to 0, 2π/3, and 4π/3, respectively.
In the numerical simulation, we first directly observe the binary sinusoidal patterns generated by the two dithering algorithms. Figure
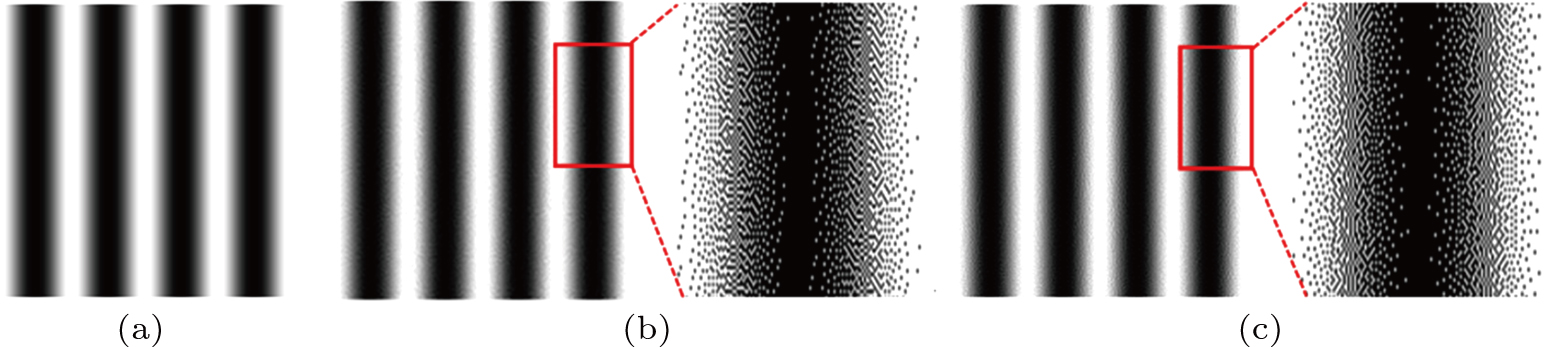 | Fig. 3 Comparison of dithered patterns by intuition. (a) Grayscale pattern; (b) Floyd–Steinberg dithered pattern; (c) Sierra–Lite dithered pattern by a serpentine scanning method. |
From Fig.
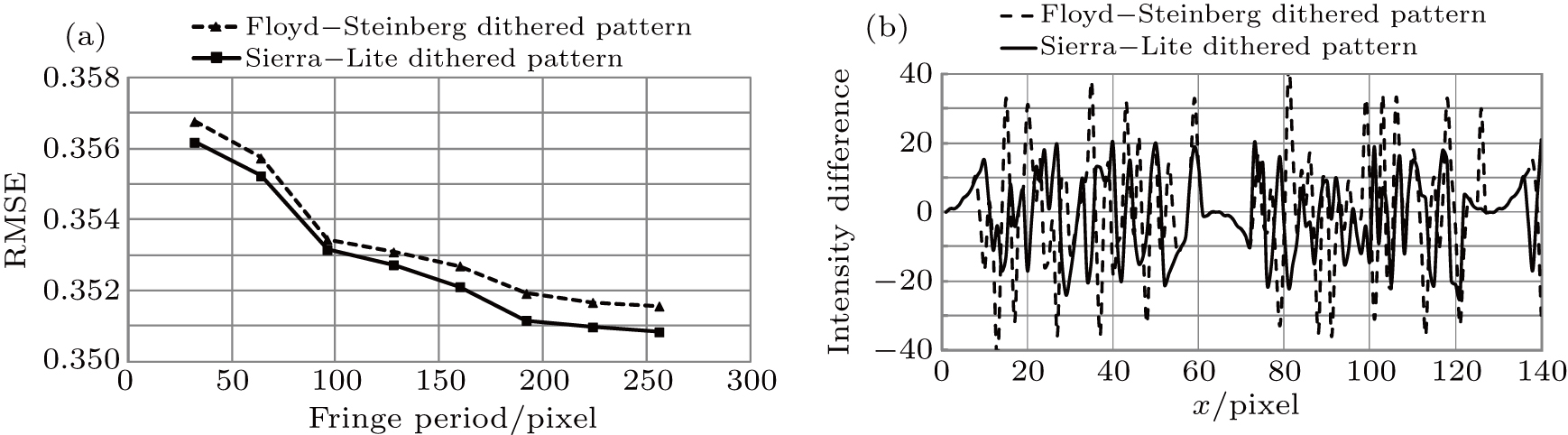
The second stage is to compare the similarity between each binary pattern and ideal grayscale sinusoidal pastern for quantitative description because higher similarity represents the excellent sinusoidality for the dithered pattern. It is certain that the Fourier spectrum of the scene image with three-step phase-shifting sinusoid illumination would be more precise. The root-mean-square error (RMSE) is applicable to describe the similarity between the dithered pattern and ideal sinusoidal pattern. Figure
It should be noted that the binary dithered pattern could be converted to grayscale by employing the defocusing techniques. Therefore, we decide to calculate any line of intensity difference to describe sinusoidality between dithered patterns after defocusing an ideal pattern. As shown in Fig.
As the results indicated in Fig.
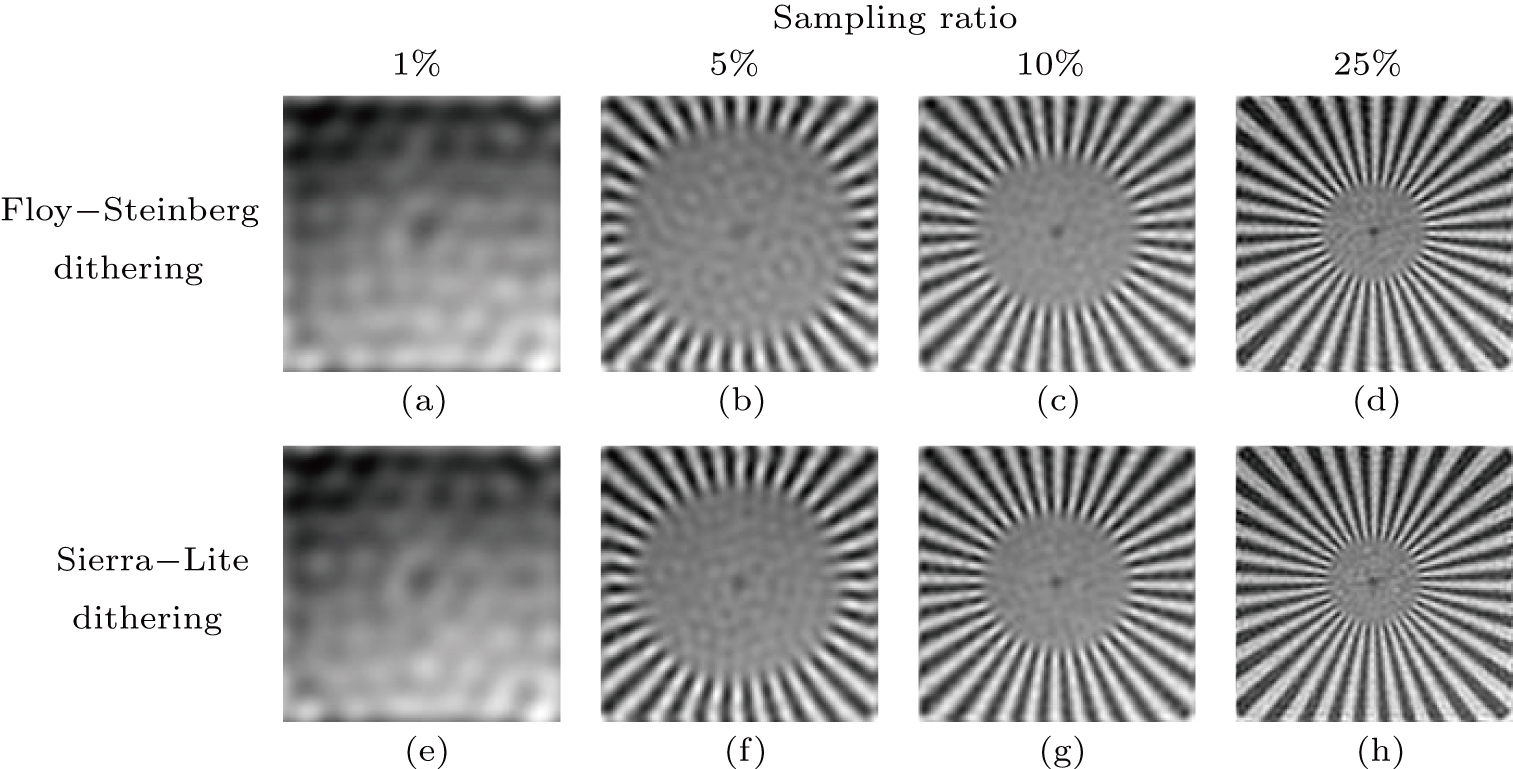 | Fig. 5 Comparison results for testpat pattern reconstruction by FSP and SLP for different sampling ratios. |
| Table 1.
Quantitative comparison results for testpat. . |
In the following simulations, we set two widely used standard 128 × 128 pixel test images, ‘testpat’ target pattern and the Lena image, as target scenes through simulation. We use peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) to quantitatively evaluate the quality of the reconstructed images. Two algorithms are implemented using Matlab on an Intel Core i5-7200 2.5-GHz CPU computer, with 8-G RAM and 64-bit Windows 10 system. Please note that, for Tables
| Table 2.
Quantitative comparison results for Lena. . |
As the results in Fig.
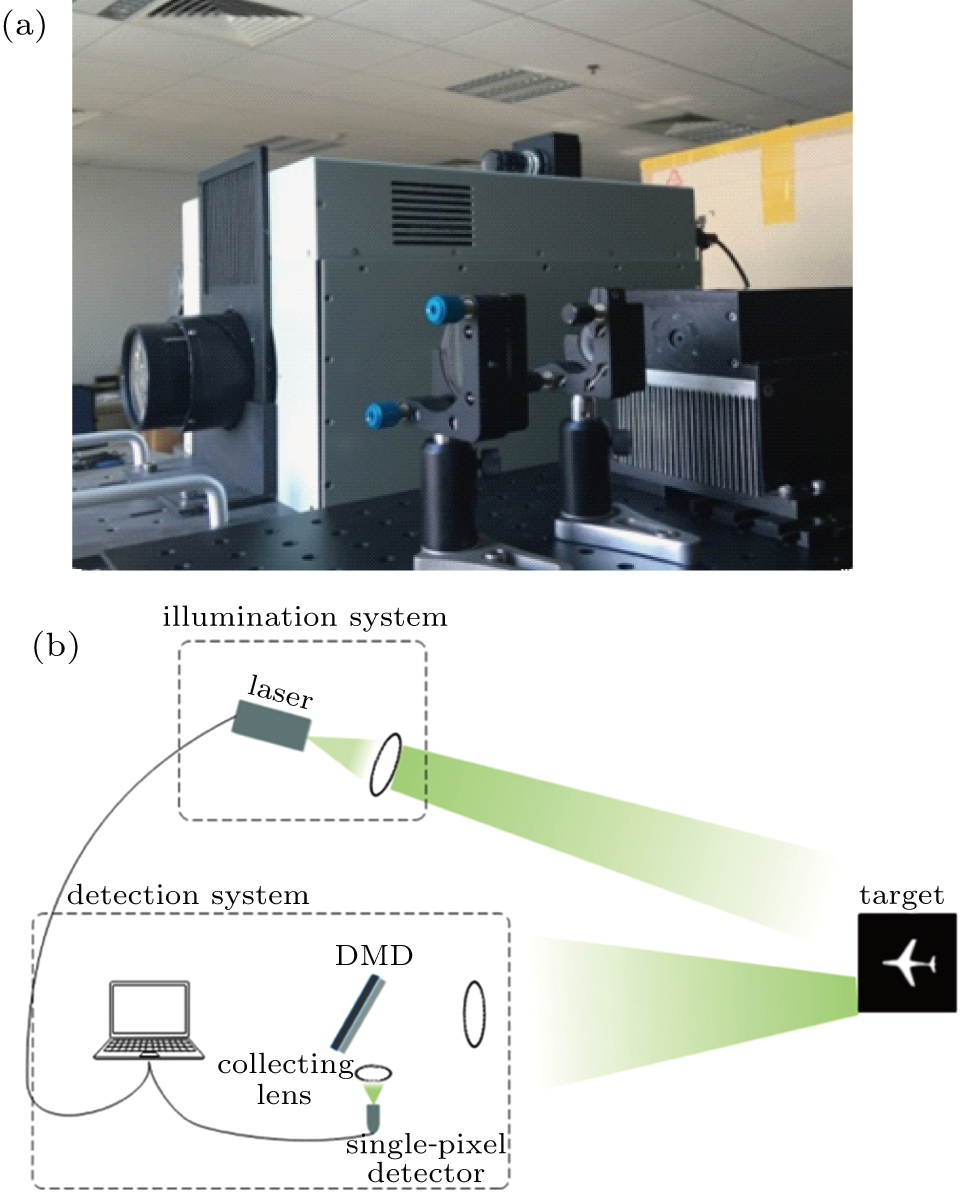
To further compare the performance of the two dithering algorithms, we have built an experimental prototype (Fig.
The results are shown in Fig.
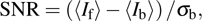 |
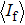
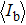
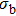
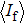
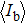
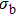
In this work, by applying an improved dithering algorithm on the structured illumination, we have managed to use Sierra–Lite kernel function by serpentine raster scanning method to improve the image quality of the binarized Fourier single-pixel imaging. We present a specific comparison between the image quality of the Floyd–Steinberg dithering algorithm and the Sierra–Lite dithering algorithm. Numerical simulation and experimental results show that the improved binary illumination pattern of the proposed algorithm has higher similarity and better sinusoidal with the grayscale patterns than the traditional binary pattern, and the reconstructed images have better image quality. To some extent, the proposed algorithm makes both low noise and high frame rate available simultaneously, and overcomes the limitation of the high speed and low-quality trade-off in binaried Fourier single-pixel imaging. It may also push forward the development of high-quality real-time single-pixel imaging.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] |