† Corresponding author. E-mail:
The structure evolution and origin of ultrahigh dielectric properties have been investigated in the low temperature range from 300 K to 5 K for [001]-oriented 0.68Pb(Mg1/3Nb2/3)O3–0.33PbTiO3 (PMN–33PT) crystal. The experimental results reveal that a short-range ordered monoclinic MA is the dominant phase at ambient temperature. As the temperature drops below 270 K, the MA transforms into monoclinic MC, and the MC remains stable until 5 K. Although no phase transition occurs from 5 K to 245 K, polar nanoregions (PNRs) display visible changes. The instability of PNRs is suggested as responsible for the low temperature relaxation. The ultrahigh dielectric constant at room temperature is associated with the instability of local structure and phase transition. Our research provides an insight into the design of high-performance ferroelectric materials.
Relaxor ferroelectric single crystals Pb(Mg1/3Nb2/3)O3–PbTiO3 (PMN–PT) with morphotropic phase boundary (MPB) are attracting considerable attention because of their outstanding piezoelectric, dielectric, and electromechanical properties. At present, it is universally considered that the polar nanoregions (PNRs) play a key role for the ultrahigh electrical properties in relaxor-PT ferroelectric crystals,[1–3] and a large number of studies have been carried out. For example, Xu et al.[4] found a strong interaction between PNRs and acoustic phonons using the neutron inelastic scattering method. They speculated that the phase fluctuation induced by PNRs should be responsible for the ultrahigh piezoelectric properties. Recently, Li et al.[5] reported the high electrical properties of relaxor-PT crystals result from the presence of PNRs. Moreover, they achieved an ultrahigh piezoelectric constant (d33 = 1500 pC/N) and dielectric constant (
The investigations into the thermodynamics of PNRs were mainly focused on above room temperature for relaxor-PT systems.[9–13] In contrast, limited studies have been reported below room temperature. Yang et al.[14] reported that the monoclinic MC transforms into monoclinic MA as the temperature decreases to 188 K, and the phase transition temperature exhibits remarkable dependence on the inhomogeneity of PNRs. Although the synchrotron x-ray and neutron diffraction results showed that the long-range MC phase in PMN–PT crystals with MPB remains stable in the temperature range from room temperature to 20 K,[15,16] thermal fluctuation in nanoscale was still proposed, and strongly affected the properties of PMN–PT crystals.[1,4–6]
The crystal structure from the synchrotron x-ray and neutron diffraction is considered to be an average structure. The local structure of PNRs is usually different from the average lattice structure of the compound. In addition, the phase-field simulations are only a theory analysis, and it will be perfect if the experimental results are in agreement with that of the theory. Micro-Raman spectrometer is a useful method to investigate the PNRs.[14,17,18] In this work, cryogenic experiments involving confocal micro-Raman spectrometer and dielectric response have been performed in low temperature range from 5 K to 300 K for nominal composition [001]-oriented 0.68Pb(Mg1/3Nb2/3)O3–0.33PbTiO3 (PMN–33PT) crystals. Our aim is to supply direct experimental evidence to demonstrate the thermodynamics of PNR and its effect on lattice and macroscopic properties, which is very useful for understanding the relationship between local structural heterogeneity and outstanding electrical properties in relaxor-PT crystals.
The 0.68Pb(Mg1/3Nb2/3)O3–0.33PbTiO3 relaxor ferroelectric single crystals were grown using the Bridgman method. The (001)-cut sample with dimensions 3 × 3 × 0.5 mm3 was prepared. The sample was polished and annealed to remove possible residual stresses. The x-ray diffraction (XRD, XRD-6000, Shimadzu Corporation, Japan) was used to certify the orientation of the sample. Then, Ag was sputtered on the (001) and (00 
Raman spectra were collected on the (001)-face of the crystal using a confocal micro-Raman spectrometer (Horiba/Jobin Yvon HR800). A solid state laser of 532 nm wavelength was used as the excitation source. The polarization direction of the incident light was parallel to the y-direction. The spectra were recorded in the parallel (VV) and crossed (VH) polarization configurations, respectively. The sample was placed inside a cryostat cell, and the temperature was changed from 305 K to 5 K.
The composition fluctuation in the as-grown PMN–PT crystals by Bridgman technique is inescapable. The PNRs are very sensitive to the composition and orientation. Figure


 | Fig. 1. The dielectric spectra of a sample in the temperature range from 290 K to 570 K: (a) dielectric constant, and (b) dielectric loss. The XRD pattern is shown in the inset of panel (a). |
Figure 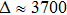
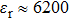
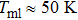
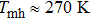

 | Fig. 2. Temperature dependence of dielectric response for [001]-oriented PMN–33PT crystal in the temperature range of 5 K to 300 K: (a) dielectric constant, and (b) dielectric loss. |
To demonstrate the existence of PNRs, the relationship between the temperature Tml and frequency f, corresponding to the dielectric loss peaks near Tml, has been investigated based on the Arrhenius law[1]
Figure
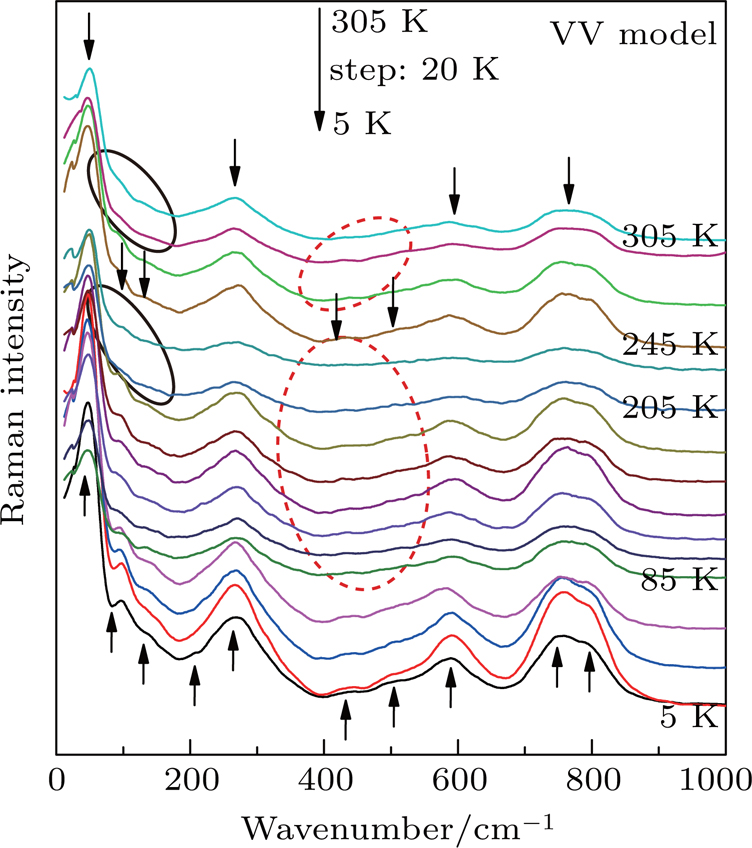 | Fig. 3. Raman spectra of [001]-oriented PMN–33PT crystal at different temperatures from 305 K to 5 K. |
It is well known that the lattice symmetry determines the number of Raman active modes, which can be used to detect the phase transitions in solids. Based on the group theory, the rhombohedral R lattice symmetry has seven Raman modes, the tetragonal T has eight, and the monoclinic M or orthorhombic O has twelve.[24] Figure
 | Fig. 4. The deconvolution of multiple Lorentzian peaks for [001]-oriented PMN–33PT crystal at specific temperatures. |
Figure
The chemical fluctuations as a result of the substitution of multiple B-site cations (Mg2+, Nb5+, and Ti4+/Ti3+) in PMN–33PT crystal induce the formation of PNRs.[3] The interaction between the PNRs and the bulk lattice can introduce an underlying structural instability,[4,26] which results in the MA phase transformation toward MC at 270 K, as shown in Fig.
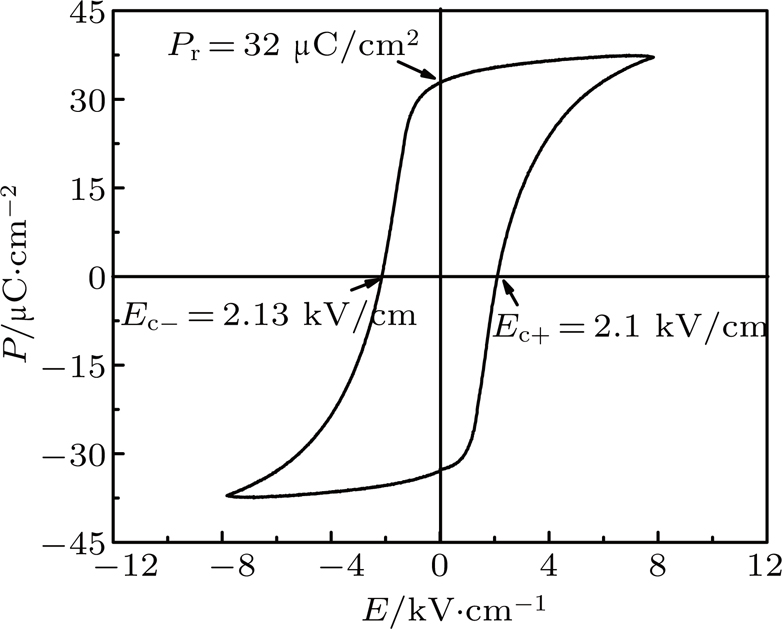
As is known, the ferroelectric and piezoelectric properties are very important for relaxor ferroelectric crystals. We have measured the piezoelectric coefficient (d33 = 2051 pC/N) and P–E loop at room temperature, as shown in Fig. 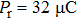
The dielectric measurement and Raman spectrum of [001]-oriented PMN–33PT crystal are collected in the low temperature range from 300 K to 5 K to investigate the evolution of microstructure and the origin of ultrahigh dielectric properties. Raman spectrum and dielectric measurement reveal that the MA is the dominant phase structure at room temperature. As the temperature drops below ambient temperature, the MA phase gradually transforms to the MC phase by an ergodic process near 270 K. No phase transition presents in the temperature range from 245 K to 5 K, suggesting the MC symmetry remains. The strong dielectric relaxor between 5 K and 245 K is attributed to the relaxational thermal dynamics of PNRs. The origin of ultrahigh dielectric constant is associated with thermal dynamics of PNRs and phase instability. The crystal shows excellent piezoelectric and ferroelectric properties d33 = 2051 pC/N and 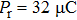
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] |