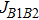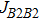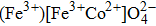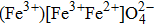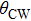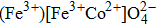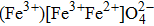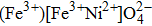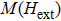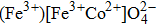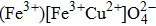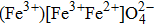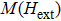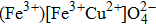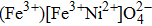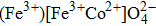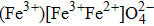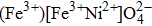† Corresponding author. E-mail:
The magnetic properties of inverse ferrite 

Cubic ferrite has the formula 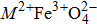
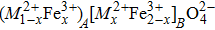
Different types of ferrite-based composites have been studied, including magnetic ferrites composed of nonmagnetic oxides and polymers.[6–8] For practical applications, however, Fe3O4 is the most promising candidate due to its high Curie temperature, TC=858 K, as compared to other half metals. These characteristics of Fe3O4 can be utilized in the development of tunneling magnetoresistance based devices that would operate at room temperature with high efficiency.[9,10] Experimentally, the properties of ferrites are dependent on the synthesis technique and synthesis conditions.[11] NiFe2O4 has the inverse spinel structure in bulk form where divalent metal ions (Ni2+) occupy octahedral sites and mixed spinel structure in case of nanoparticles where Ni2+ ions can occupy both tetrahedral and octahedral sites.[12] CuFe2O4 is ferromagnetically ordered for a weak magnetic field and it has wide applications due to its high thermal stability.[13] Nickel ferrite NiFe2O4 is a good example of inverse spinel ferrite and exhibits ferromagnetic nature with a Curie temperature of 858 K where half of the Fe3+ ions occupy the tetrahedral sites and the remaining ions occupy the octahedral sites, it is used in repulsive suspension for levitated railway systems, microwave absorber, magnetic liquids, magnetic refrigeration, and high density magnetic recording media.[14,15] In previous work,[16] the CoFe2O4 nanowire arrays become superparamagnetic at 600 K. High magnetostriction and strain-field derivative with low saturation field make (0 0 1) fiber textured CoFe2O4 attractive for sonar detector and force sensor applications.[17] Theoretically, the formation condition and energy of possible intrinsic point defects have been investigated by the first-principles calculations, and the effects of the intrinsic point defects on the electronic and magnetic properties of CoFe2O4 have been analyzed.[18] The experimental and numerical results using Monte Carlo simulation of the reduced magnetization and coercivity cobalt ferrite/polyvinylpyrrolidone are in relatively good agreement with each other.[19] The first-principles, mean-field, and series expansions calculations have been used to study the electronic and magnetic structures of Fe3O4.[20] Green’s function theory has been used to study the magnetic properties of CuxNi1−xFe2O4 spinels.[21] The effect of Zn doping on magnetic properties of MnFe2O4 ferrite spinel has been studied by using high temperature series expansion combined with the Padé approximant and mean field theory.[22] In the previous work,[23] silicene is an intriguing two-dimensional (2D) topological material which is closely analogous to graphene but with stronger spin–orbit coupling effect and natural compatibility with current silicon-based electronic industry. It could realize a ferromagnetic phase, super-counter-fluidity phase, and antiferromagnetic phase of polarized light that are of interest for studying spin-dependent photon-photon interactions.[24] The effect of spin transport on nonlinear excitations was investigated in a ferromagnetic nanowire with nonuniform magnetizations.[25]
In the present work, we have used the Monte Carlo simulation to study the magnetic properties of inverse ferrite 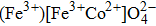

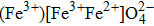
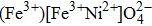
In inverse spinel ferrites 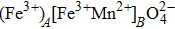



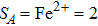
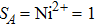

The values of exchange interactions JAA, 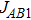

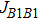


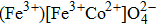
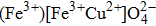
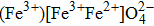

| Table 1.
The values of exchange interactions used in this work for the spinels. . |
The Fe3+(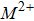

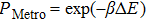
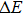


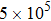
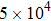
The total internal energy is given by
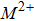
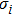

In the present work, we have used the Monte Carlo simulation to study the magnetic properties of inverse ferrite 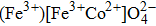


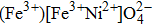

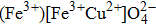
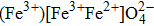
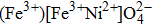
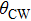

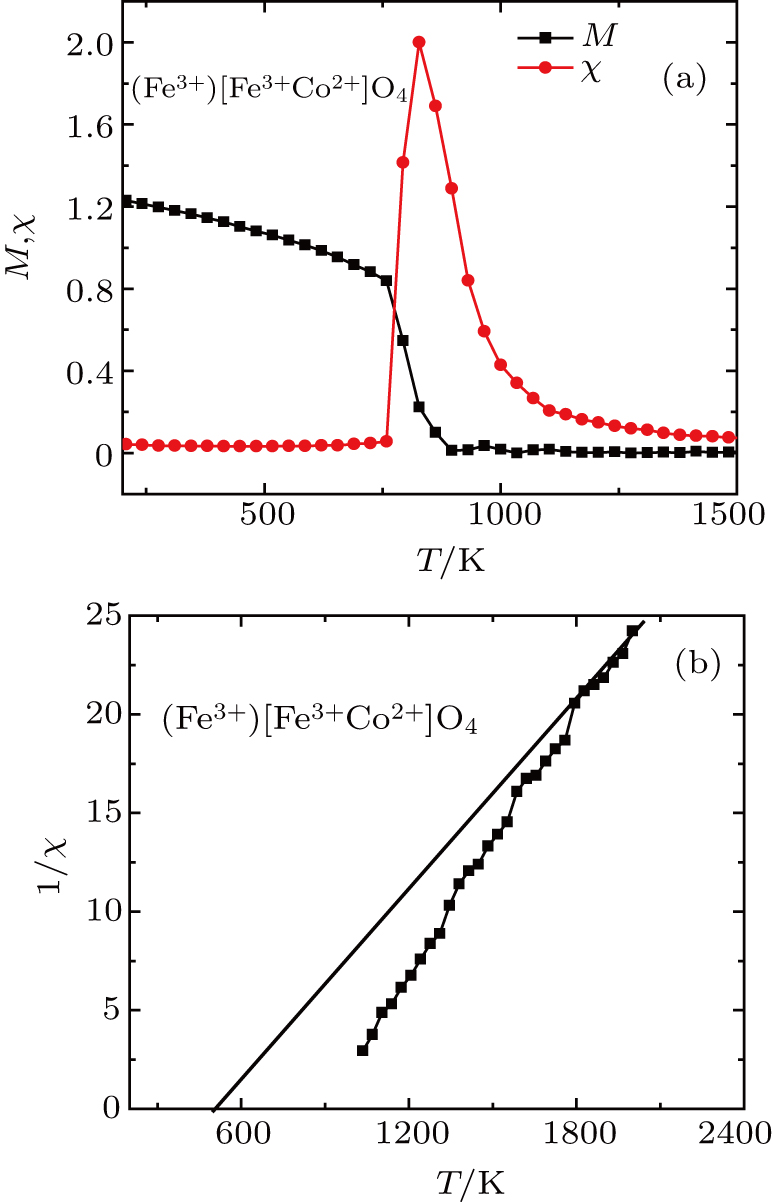 | Fig. 1. (a) The thermal magnetization and magnetic susceptibility and (b) inverse magnetic susceptibility of 
|
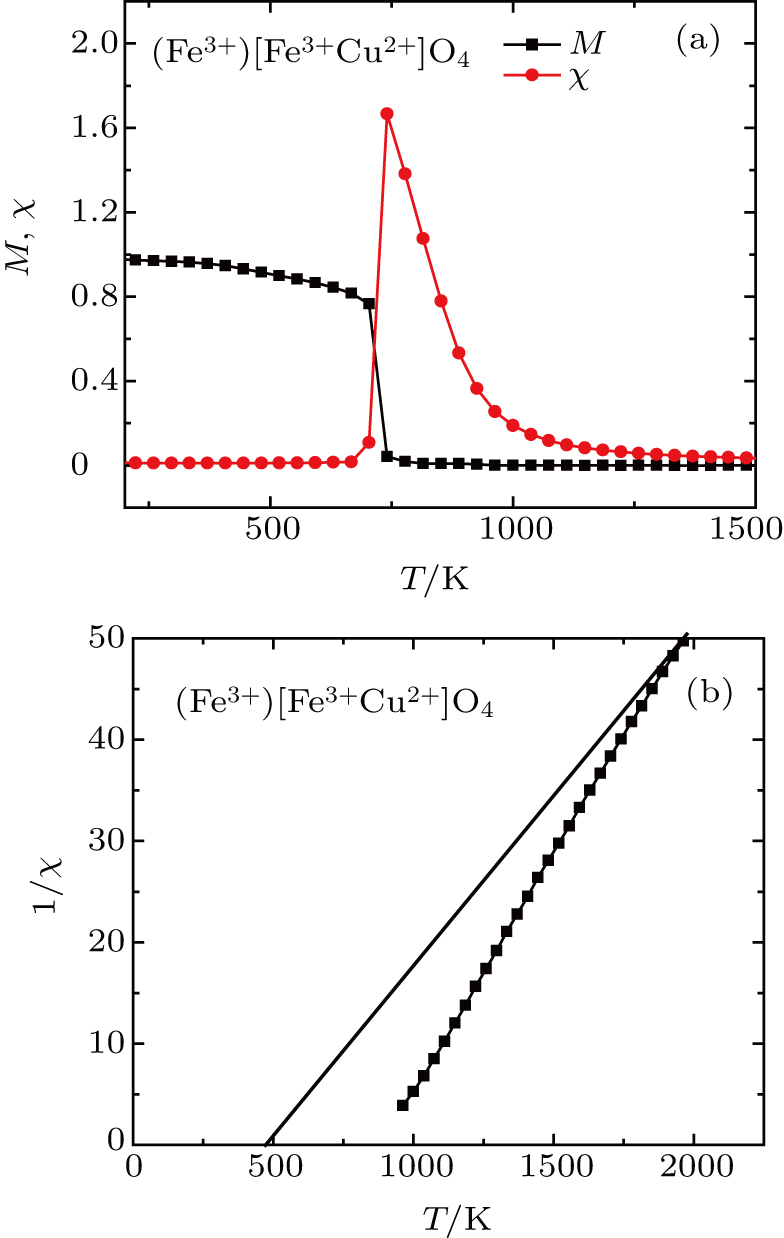 | Fig. 2. (a) The thermal magnetization and magnetic susceptibility and (b) inverse magnetic susceptibility of 
|
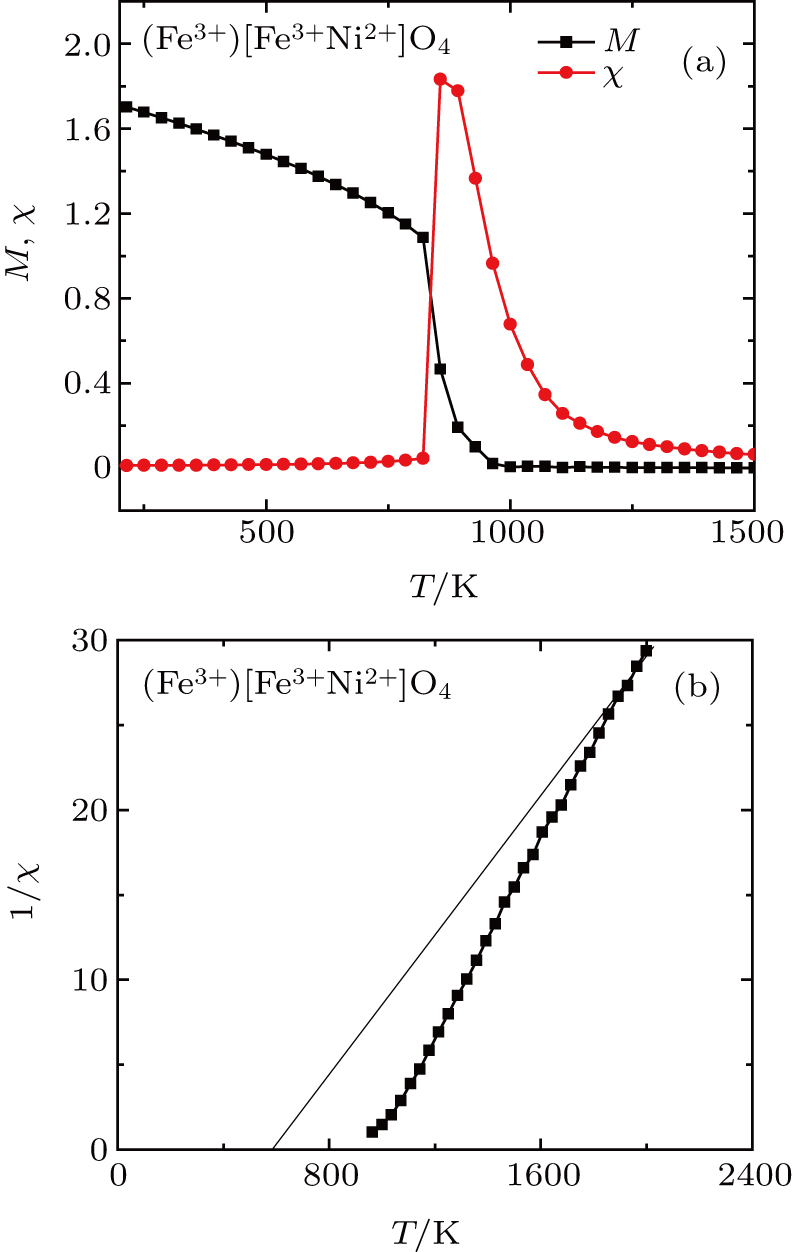
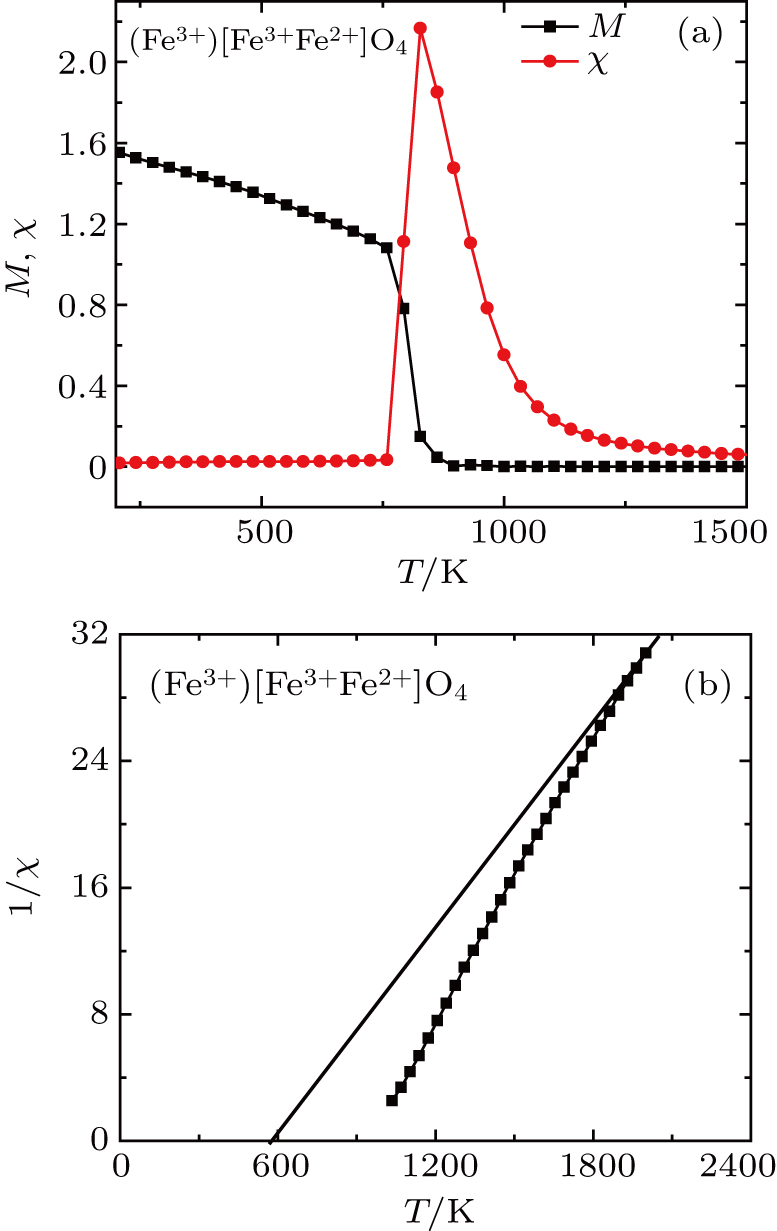 | Fig. 3. (a) The thermal magnetization and magnetic susceptibility and (b) inverse magnetic susceptibility of 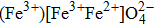
|
 | Fig. 4. (a) The thermal magnetization and magnetic susceptibility and (b) inverse magnetic susceptibility of 
|
| Table 2.
The critical and Curie Weiss temperatures obtained by Monte Carlo simulations, experiments (Ref. [25] for TC and Ref. [29] for |
The magnetic 
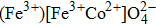
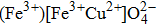

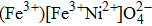
 | Fig. 5. (a) Magnetic 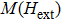
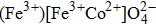
|
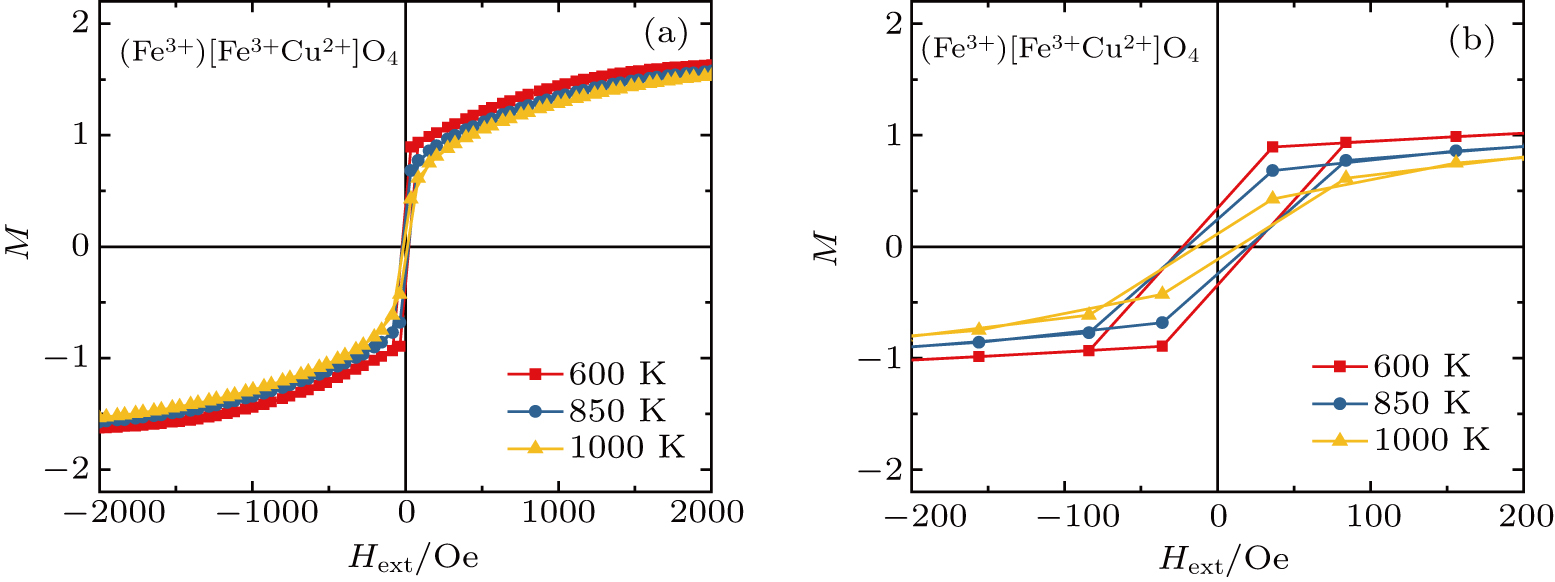 | Fig. 6. (a) Magnetic 
|
 | Fig. 7. (a) Magnetic 

|
 | Fig. 8. (a) Magnetic 
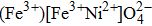
|
Figure 

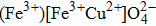

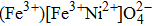
We have calculated the critical exponents β, γ, and δ associated with the magnetization, magnetic susceptibility, and external magnetic field using Eq. (
| Table 3.
The critical exponents |
The magnetic properties of inverse ferrite 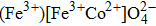
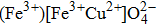

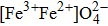
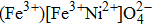

| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] |