† Corresponding author. E-mail:
Low thermal expansion materials are mostly ceramics with low conductive property, which limits their applications in electronic devices. The poor conductive property of ceramic ZrV2O7 could be improved by bi-substitution of Fe and Mo for Zr and V, accompanied with low thermal expansion. Zr0.1Fe0.9V1.1Mo0.9O7 has electrical conductivity of 8.2×10−5 S/cm and 9.41×10−4 S/cm at 291 K and 623 K, respectively. From 291 K to 413 K, thermal excitation leads to the increase of carrier concentration, which causes the rapid decrease of resistance. At 413–533 K, the conductivity is unchanged due to high scattering probability and a slowing increase of carrier concentration. The conductivity rapidly increases again from 533 K to 623 K due to the intrinsic thermal excitation. The thermal expansion coefficient of Zr0.1Fe0.9V1.1Mo0.9O7 is as low as 0.72×10−6 K−1 at 140–700 K from the dilatometer measurement. These properties suggest that Zr0.1Fe0.9V1.1Mo0.9O7 has attractive application in electronic components.
Metal materials have excellent conductivity, but their thermal expansion property could induce thermal stress and even function failure. Meanwhile, ceramic materials have low thermal expansion coefficients but their conductivities are usually poor. Recent investigations suggest that negative thermal expansion materials could be used to prepare low thermal expansion materials by partial ion substitution, doping, or compounding with positive thermal expansion materials,[1–3] which could also result in high conductivity.[4–8]
ZrV2O7 is one of the isotropic negative thermal expansion materials but its negative thermal expansion is only present after a phase transition.[9] P5+ ion has been used to substitute V5+ in ZrV2O7 to decrease the phase transition temperature and realize low thermal expansion. ZrV2−xPxO7 (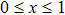
ZrV2O7 has poor conductivity at room temperature (RT), which is increased with increasing temperature (σ = 3.56×10−3 S/cm at 573 K).[13,17] The introduction of Cs in ZrV2O7 could enhance the ionic conductivity. Charge transport in VO4 could provide the observed high ionic conductivity.[18,19] In this paper, dual-ion substitutions of Fe3+/Mo6+ for Zr4+/V5+ in ZrV2O7 are investigated to increase the conductivity of ZrV2O7. Zr0.1Fe0.9V1.1Mo0.9O7 is found with electrical conductivity σ = 8.2 ×10−5 and 9.41 ×10−4 S/cm at 291 K and 623 K, and activation energy Ea = 0.160 eV and 0.233 eV for 291–413 K and 533–623 K, calculated from the Arrhenius plots for the total conductivity.
Zr0.1Fe0.9V1.1Mo0.9O7 was synthesized by a solid state method with raw materials Fe2O3, ZrO2, MoO3, and V2O5. The raw materials were mixed according to stoichiometric amounts of Zr0.1Fe0.9V1.1Mo0.9O7 (with excess 5 mol% V2O5) and ground in a mortar for 3 h. The homogenized raw materials were pressed into 10 mm ×2.5 mm (diameter ×height) cylindrical pellets, sintered in a tubular furnace at 5 K/min heating rate, held at 953 K for 2–5 h, and then cooled down slowly to RT.
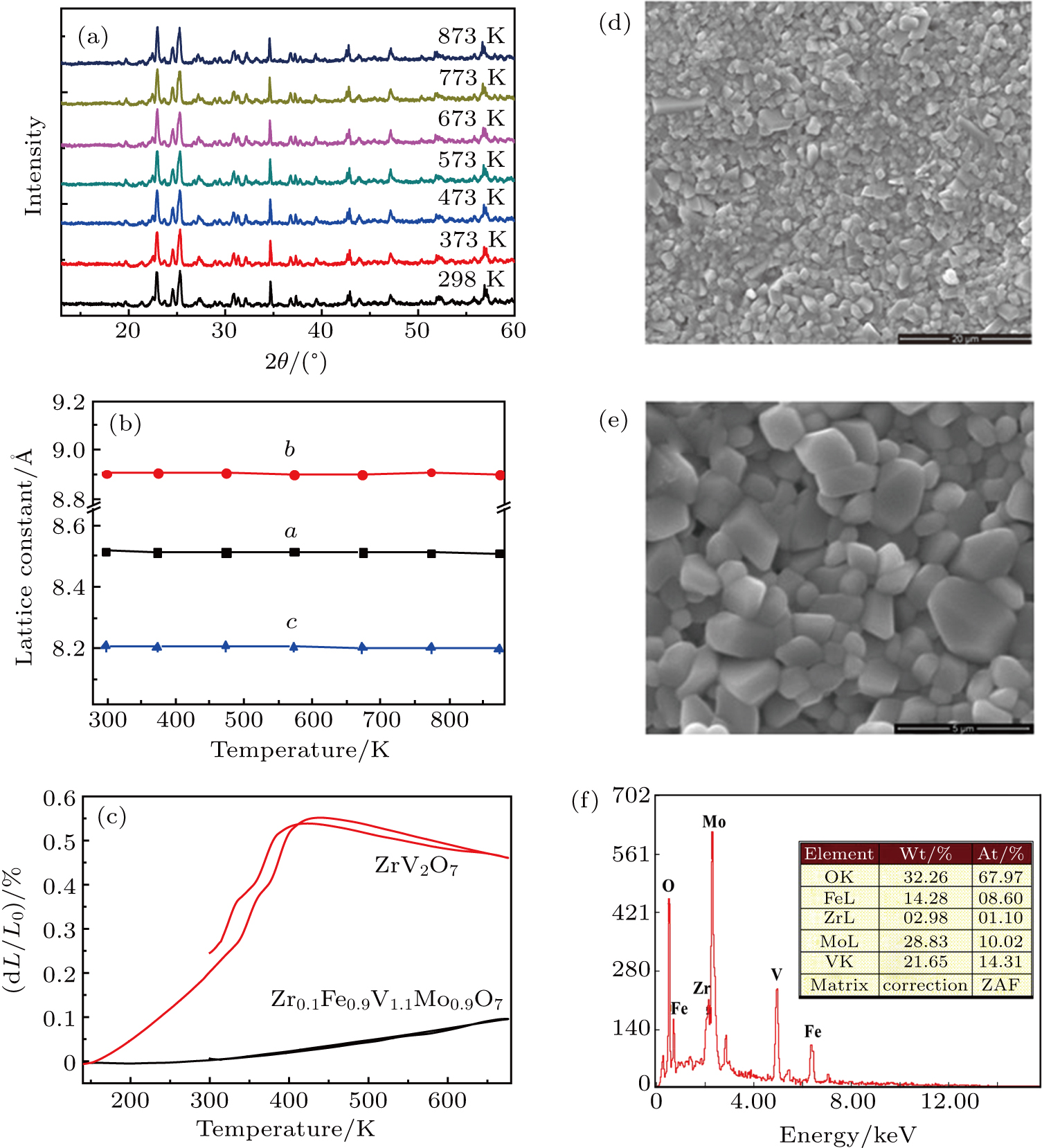
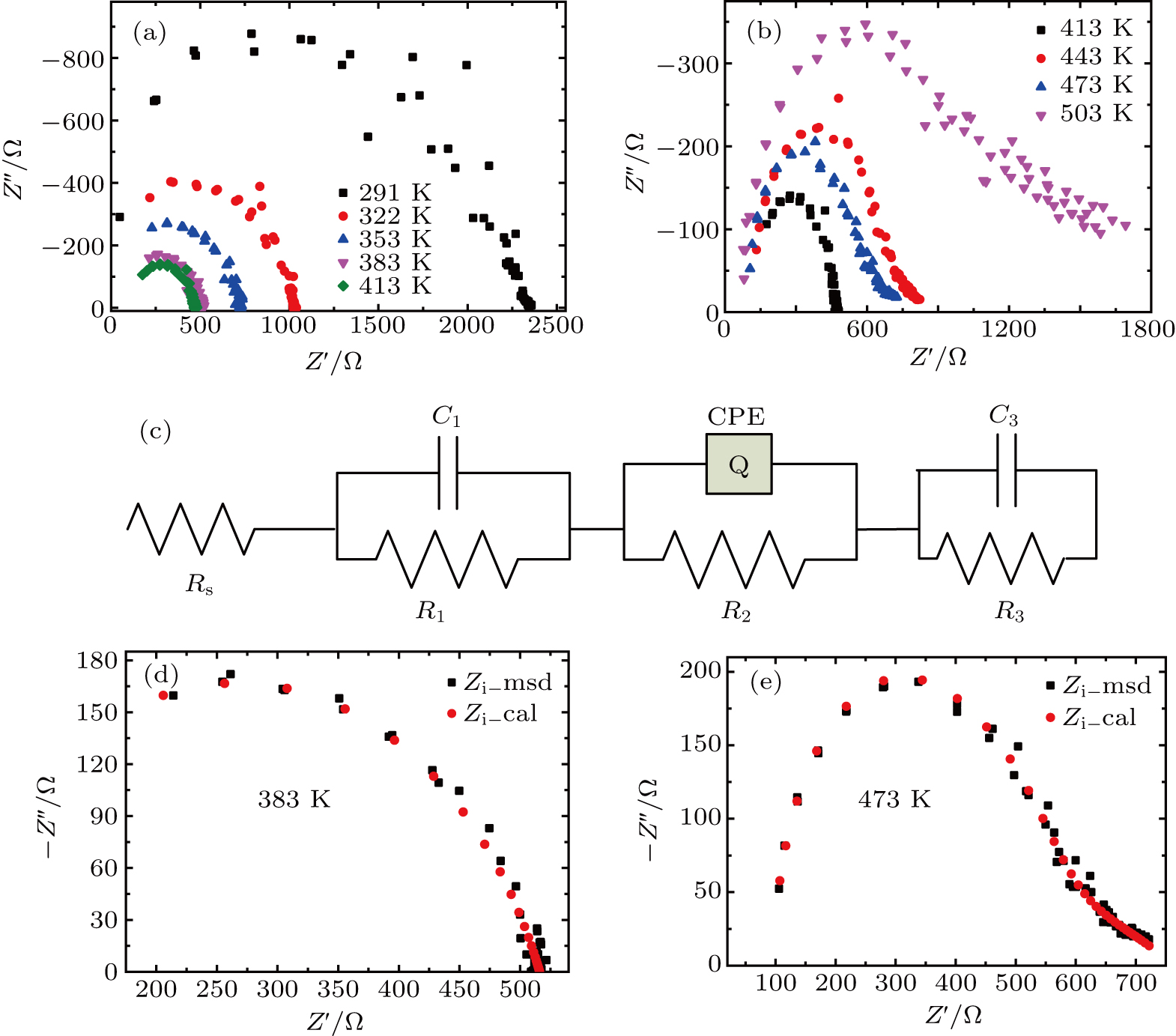
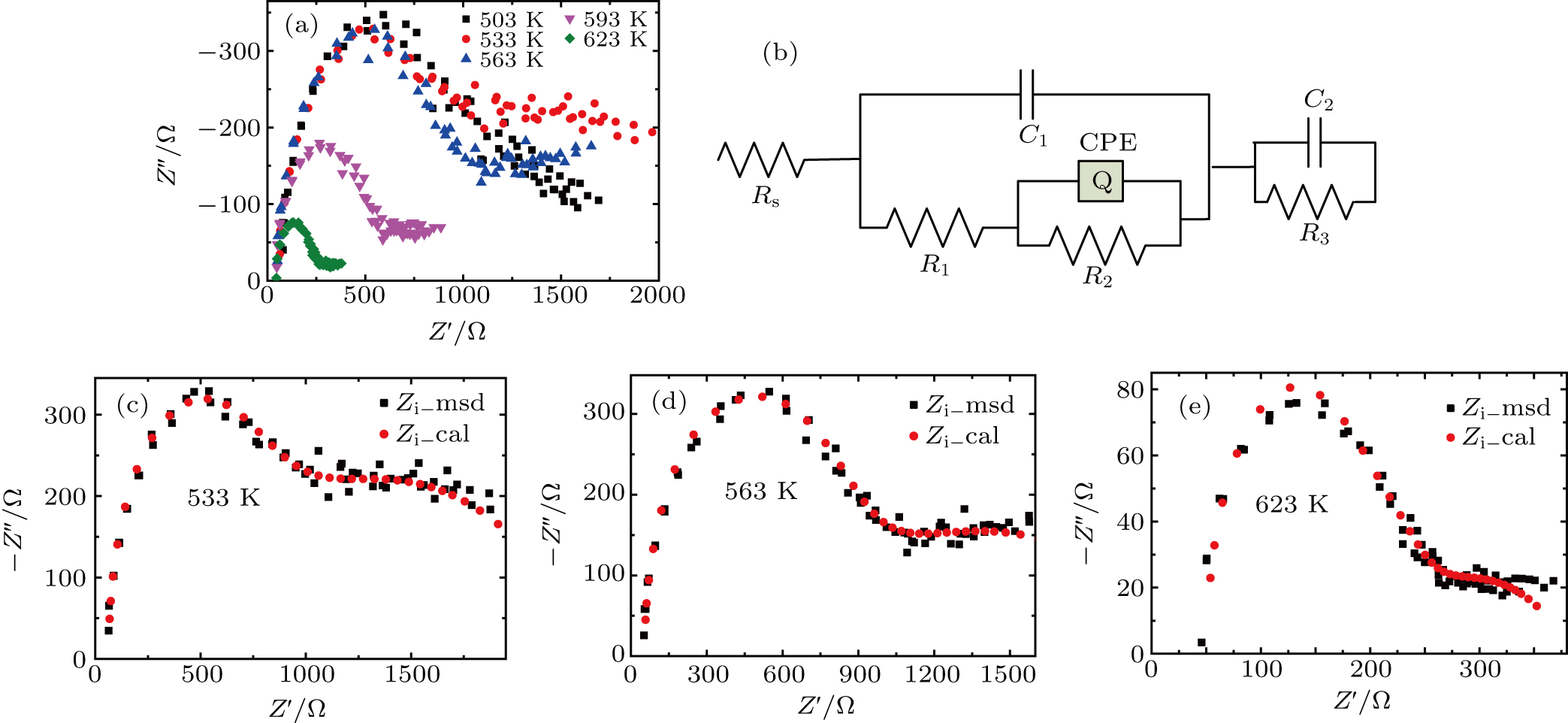
X-ray diffraction (XRD, Bruker D8 Advance Diffractometer) was used to analyze the crystal phase of the sample. Microstructures were checked using scanning electron microscopy (SEM, JSM-6700 F) and elements were analyzed with energy dispersive spectrum (EDS). Pellet electrical conductivity was measured after polishing and coating both surfaces with Ag paste. Complex impedance was measured using a frequency response analyzer (1 Hz to 4 MHz) in the temperature range from RT to 623 K. The linear thermal expansion coefficients were measured on dilatometers (LINSEIS DIL L75), with heating and cooling rates of 5 K/min.
Figure
Figures 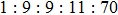
Figure
 |
 |
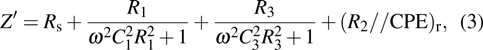 |
 |
Figure
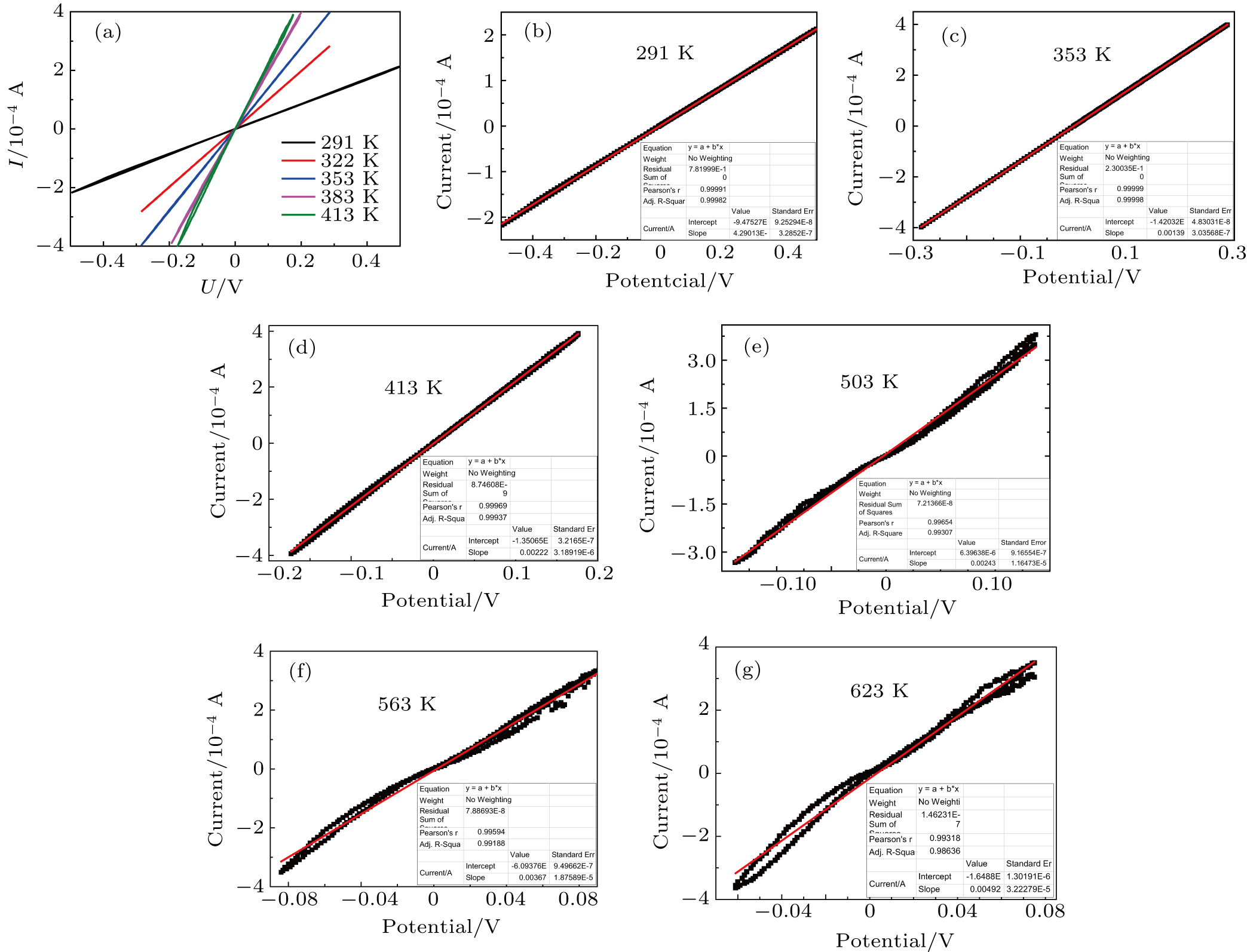
To obtain appropriate resistance dependence on temperature, we measured direct-current (DC) current–voltage (I–V) characteristics of Zr0.1Fe0.9V1.1Mo0.9O7 at different temperatures (Fig. 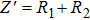
The conductivity σ can then be calculated from[25]
 |
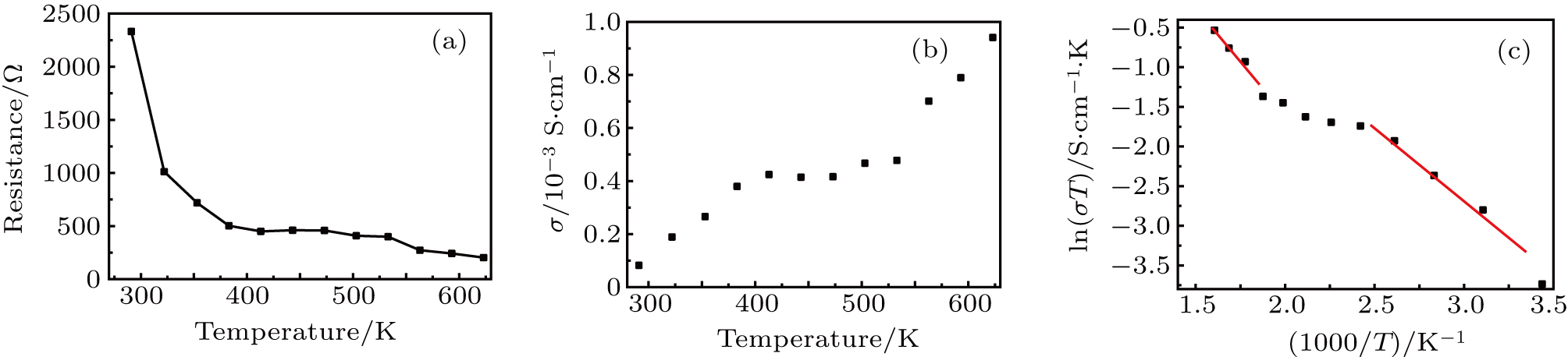 | Fig. 5. Zr0.1Fe0.9V1.1Mo0.9O7 total electrical resistance (a) and (b) conductivity, and (c) Arrhenius plots for the total conductivity. |
Arrhenius plots for Zr0.1Fe0.9V1.1Mo0.9O7 in normal atmosphere. The values of σ are calculated to be 8.2 ×10−5 S/cm, 3.80 ×10−4 S/cm, 4.16 ×10−4 S/cm, and 9.41 ×10−4 S/cm at 291 K, 383 K, 473 K, and 623 K, respectively. The linear relationship of conductivity with temperature (Fig. 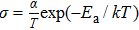
Carrier concentration could be controlled by temperature.[26–28] The conductivity of Zr0.1Fe0.9V1.1Mo0.9O7 is larger than that of ZrV2O7.[14] This could be related to the substituting effect of Fe3+/Mo6+ for Zr4+/V5+ in ZrV2O7, like p type doping (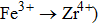
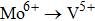


Zr0.1Fe0.9V1.1Mo0.9O7 shows near zero thermal expansion and high conductivity. The conductivities of Zr0.1Fe0.9V1.1Mo0.9O7 are 8.2×10−5 S/cm, 3.80×10−4 S/cm, 4.16×10−4 S/cm, and 9.41×10−4 S/cm at 291 K, 383 K, 473 K, and 623 K, respectively. The electrical conductivity is linear for 291–413 K, and the activation energy is 0.160 eV. At 533–623 K, the activation energy is 0.233 eV, indicating that Zr0.1Fe0.9V1.1Mo0.9O7 acts like a classical doped semiconductor. Thermal excitation leads to carrier concentration increase from RT to 413 K, which leads to a rapid resistance decrease. The unchanged conductivity during 413–533 K is due to high scattering probability and slowing-down increase of carrier concentration. The intrinsic thermal excitation leads to rapid increase of conductivity at 533–623 K.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] |