† Corresponding author. E-mail:
We investigate the dynamics of airy beams propagating in the parity–time (PT) symmetric optical lattices in linear and nonlinear regimes, respectively. For the linear propagation, the position of the channel guided by the PT lattice can be shifted by tuning the lattice frequency. The underlying physical mechanism of this phenomenon is also discussed. An interesting phenomenon is found in the nonlinear regime in that the airy beam becomes a tilt channel with several Rayleigh lengths. These findings create new opportunities for optical steering and manipulations.
According to the traditional theory of quantum mechanics, there is a basic assumption that all operators corresponding to observable physical quantities are Hamiltonian with real eigenvalues. However, in 1998, Bender and Boettcher[1] showed in a seminal work that this assumption needs to be further refined and introduced the concept of parity–time (PT-symmetric) complex-valued potentials. They found that non-Hermitian Hamiltonians can still have entirely real eigenvalue spectra provided that these Hamiltonians respect the PT symmetry. Even though examples of such operators have been known for a long time, Bender and Boettcher's (1998) discovery had profound implications because it suggested a possibility of PT-symmetric modification of the conventional quantum mechanics that considers observables as Hermitian operators in the Hilbert space L2.
It was also demonstrated that these types of Hamiltonians can undergo a phase transition above a critical threshold; i.e., a spontaneous PT symmetry breaking. Above this transition point, the eigenvalue spectrum is no longer entirely real but is rather partially complex.[2–4] So for a general Hamiltonian, one proves that a necessary condition for the Hamiltonian to be PT-symmetric is 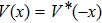
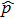
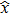
In the theoretical arena, the early promotive work of Musslimani et al.[5] studied the effect of Kerr nonlinearity on the unique beam dynamics in PT-symmetric complex-valued periodic optical potentials; i.e., the formation of nonlinear self-trapped modes, alias optical solitons in both one-dimensional (1D) and two-dimensional (2D) PT-symmetric synthetic linear optical lattices. The study of PT-symmetric linear optical lattices[6,7] has also attracted much attention during the past few years. Beam dynamics in PT-symmetric complex-valued periodic lattices can exhibit unique characteristics, such as double refraction, power oscillations, nonreciprocal diffraction patterns, and so on.[6] Furthermore, gap solitons in parity–time complex-valued periodic optical lattices with the real part of the linear lattice potential having the shape of a double-periodic function (a super lattice potential) were studied by Zhu et al.[8] Guo and his scientific research team's finding provided the first example of embedded solitons in 2D PT periodic systems.[9] From both theoretical and experimental points of view, the investigation of beam dynamics in nonlinear symmetric systems is essential. Konotop et al. comprehensively reviewed recent progress on nonlinear properties of PT-symmetric systems.[10] In their complete work, nonlinear PT-symmetric systems arising from various physical disciplines are presented, nonlinear properties of these systems are thoroughly elucidated, and relevant experimental results are described.
Recently, the dynamics of beams in PT-symmetric optic lattices have been extensively studied,[6,8–13] but there many directions are still to be explored, especially the dynamics of special nondiffracting beams in PT-symmetric optic lattices have seldom been studied. Jones took the Mathieu function as an example to show the use of equivalent Hermitian Hamiltonian for PT-symmetric sinusoidal optical lattices.[14] To the best of our knowledge, the dynamics of Airy beam in PT-symmetric optical lattices have never been studied. Compared to Mathieu beams, in addition to its quasi-diffraction-free [15] and self-healing properties,[16] the Airy beam has the singular properties of self-bending propagation. Christodoulides first experimentally implemented an Airy beam in 2007.[17,18] Due to its special properties, the Airy beam quickly attracted the attention of researchers.[19–31] In this paper, the dynamics of airy beams propagating in the PT-symmetric optical lattices are investigated both in linear and nonlinear regimes, respectively. For the linear propagation, it is shown that the position of the channel guided by the PT lattice can be shifted via tuning the lattice frequency. The underlying physical mechanism of this phenomenon is also discussed. An interesting phenomenon is found in the nonlinear regime—the airy beam becomes a tilt channel with several Rayleigh lengths.
We consider the nonlinear Schrödinger equation with a complex potential modulated by the refractive index and the gains and/or losses in transverse direction. The normalized equation can be described in the form
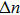
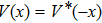
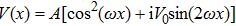
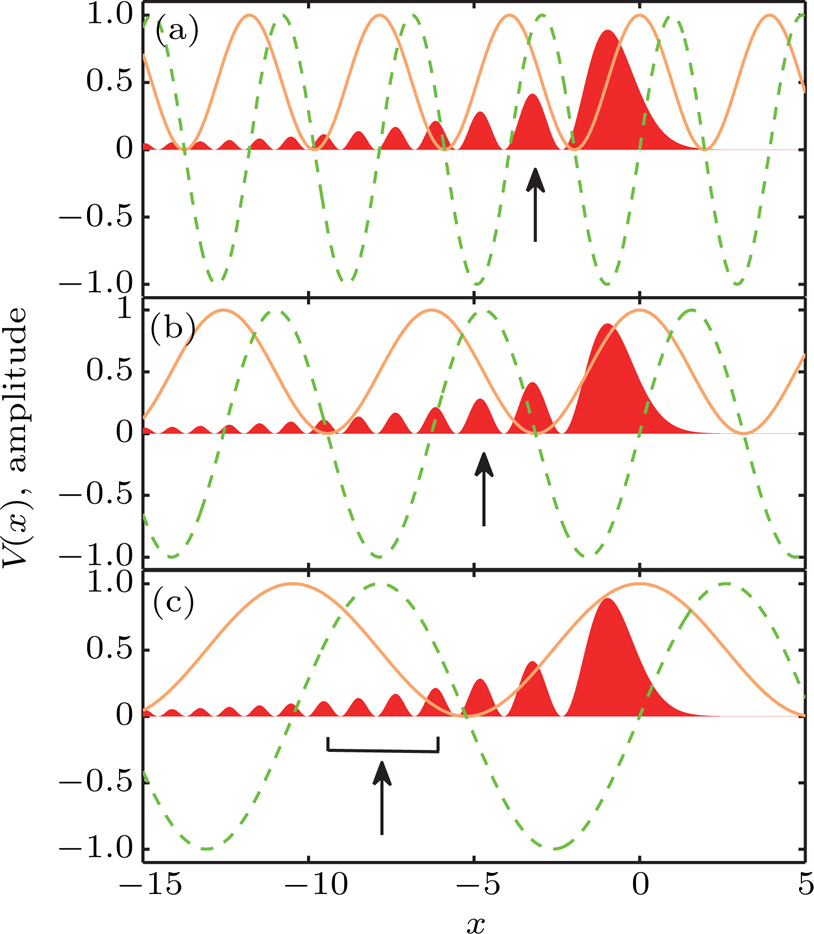
In this paper, the input Airy beams propagating in the PT-symmetric lattices can be expressed as 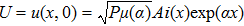
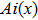
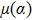
To see how the PT symmetric optical lattices impact on the Airy beam, we first consider the propagation of the Airy beam in the PT lattices in the linear regime by setting 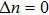
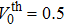
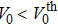

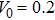
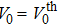

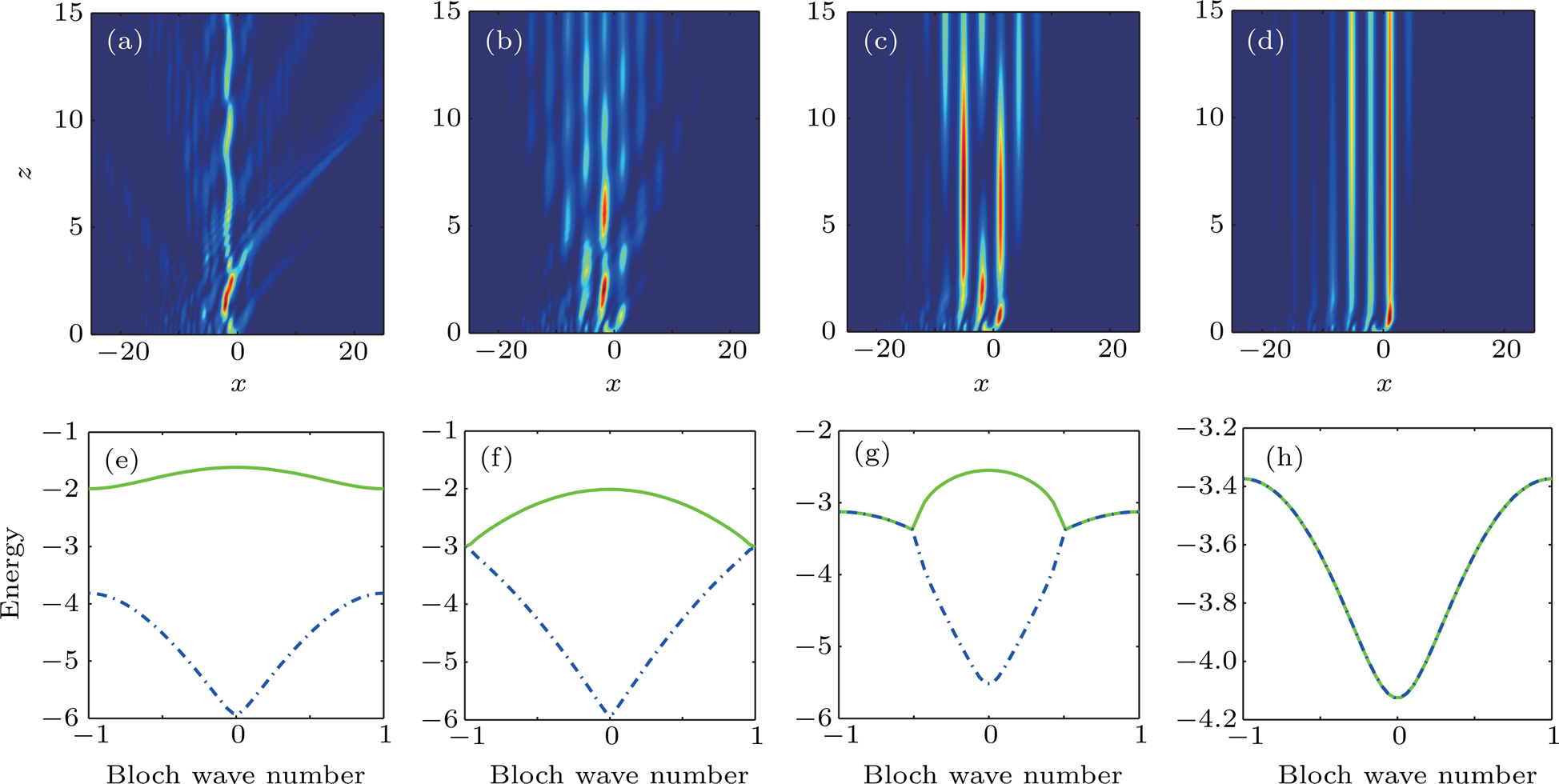
Next, we consider the evolutions of the Airy beam in the lattices with different lattice frequencies under the condition that V0 is much larger than the threshold. Note that the threshold decreases when reducing the lattice frequencies. An interesting phenomenon is found that the main channel guided by the lattice is shifted to the minus direction of the transverse coordinate x, as depicted in Fig.
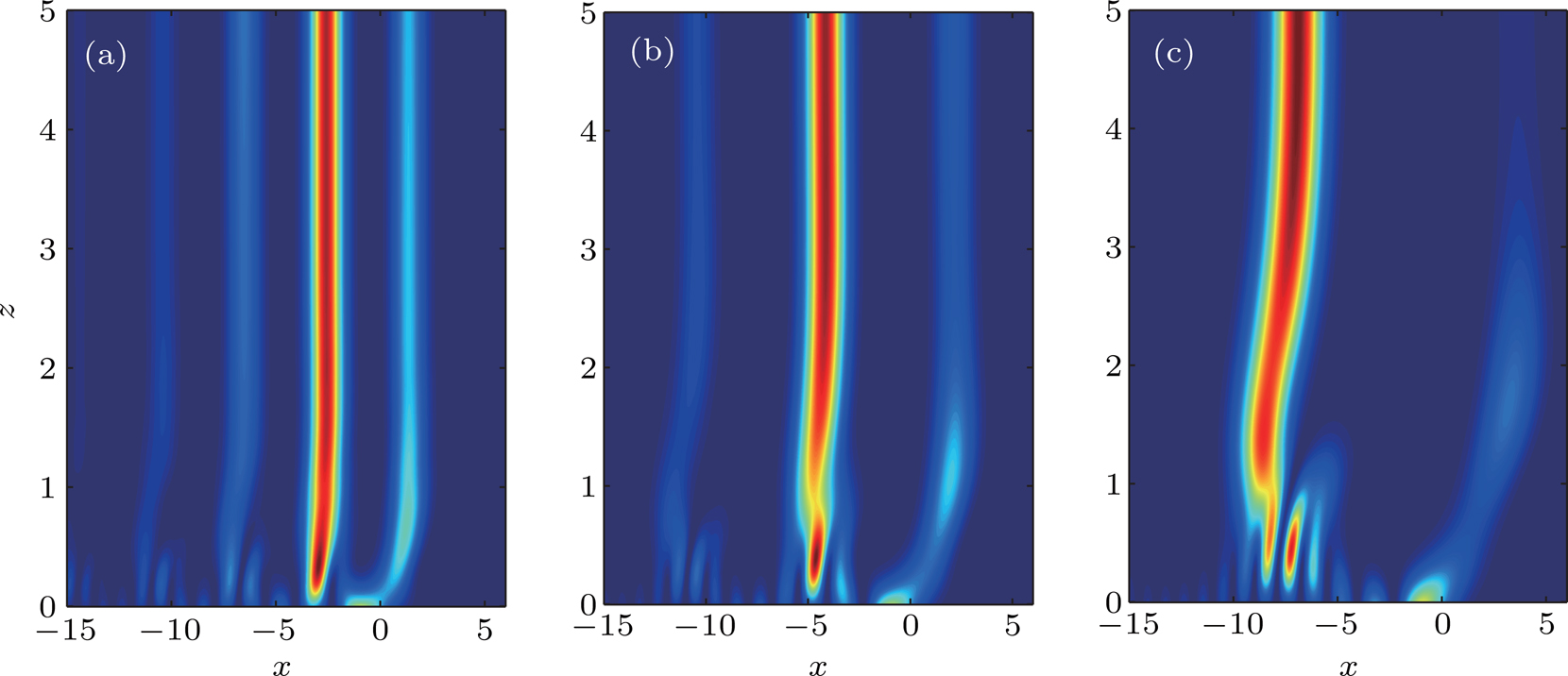 | Fig. 2. The evolutions of the Airy beam in the PT lattices for the cases of (a) ω=0.8, (b) ω=0.5, and (c) ω=0.3. V0 is fixed to 1. |
If the nonlinearity is considered, the propagation of the Airy Beam in the PT lattices becomes rather complicated. The results are shown in Figs. 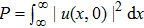

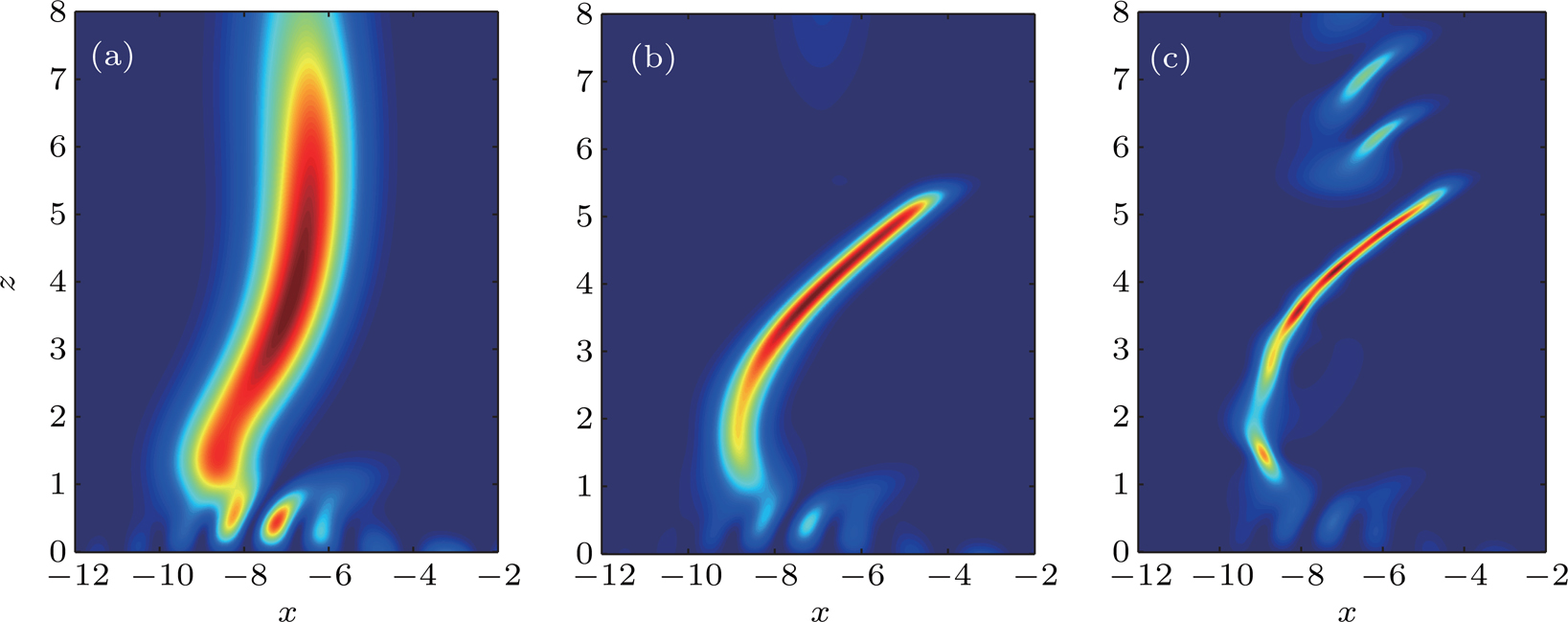 | Fig. 4. The evolutions of the Airy beam in the PT lattices for (a) P = 1, (b) P = 5, and (c) P = 9. Other parameters are set as V0=1 and ω=0.3 in the simulation. |
The tilted channel is also manipulated by the frequency of the lattice. The results are shown in Figs.
We investigate the dynamics of airy beams propagating in the parity–time symmetric optical lattices in both linear and nonlinear regimes. For the linear propagation, it is shown that the position of the channel guided by the PT lattice can be shifted via tuning the lattice frequency, which is due to the energy gain of the selective sub-loop(s). An interesting phenomenon is found in the nonlinear regime that the airy beam turns to be a tilt channel with several Rayleigh lengths. These findings create new opportunities for optical steering and manipulations.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] |