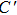Cite this Article
Zhang Ning-Ning, Zhang Yu-Juan, Yang Yu, Zhang Ping, Ge Chang-Chun. First-principles study of structural, mechanical, and electronic properties of W alloying with Zr. Chinese Physics B, 2019, 28(4): 046301  
Permissions
First-principles study of structural, mechanical, and electronic properties of W alloying with Zr
Zhang Ning-Ning1, Zhang Yu-Juan1, †, Yang Yu2, Zhang Ping2, Ge Chang-Chun1, ‡
School of Materials Science and Engineering, University of Science and Technology Beijing (USTB), Beijing 100083, China
LCP, Institute of Applied Physics and Computational Mathematics, Beijing 100088, China

 

† Corresponding author. E-mail: zhangyujuan@ustb.edu.cn ccge@mater.ustb.edu.cn

Abstract

The structural, mechanical and electronic properties of W1−xZrx (x = 0.0625, 0.125, 0.1875, 0.25, 0.5) are systematically investigated by means of first-principles calculation. The total-energy calculations demonstrate that the W–Zr binary substitutional solid solution remaining bcc structure can be formed at an atom level. In addition, the derived bulk modulus (B), shear modulus (G), Youngʼs modulus (E) for each of W–Zr alloys decrease gradually with the increase of Zr concentration, suggesting that W alloying with higher Zr concentration becomes softer than pure W metal. Based on the mechanical characteristic B/G ratio, Poissonʼs ratio υ and Cauchy pressure 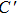, all W1−xZrx alloys are regarded as ductile materials. The ductility for each of those materials is improved with the increase of Zr concentration. The calculated density of states indicates that the ductility of W1−xZrx is due to the fact that the bonding in the alloy becomes more metallic through increasing the Zr concentration in tungsten. These results provide incontrovertible evidence for the fact that Zr has a significant influence on the properties of W.

PACS: 63.20.dk;64.70.kd;87.19.rd
Keyword:first-principles calculation;tungsten;zirconium;elastic properties
1. Introduction

Tungsten (W) has many applications because it has the highest melting point of all of the elements, it also has a high elastic modulus, high density, high thermal conductivity, and excellent mechanical properties at elevated temperatures, such as in incandescent light bulb filaments, heating elements, and kinetic energy penetrators.[1] The study of W is important for plasma facing material due to its high melting point, high strength at high temperatures and high plasma sputtering erosion resistance.[2–4] However, the poor ductility of tungsten is not conducive to its workability and performance in the applications. Thus, there is an urgent need to improve the mechanical properties of tungsten.

To date, doping impurities and additives in W has been demonstrated to be a promising method to improve physical properties. For example, it is well-accepted that alloying zirconium (Zr) could improve the physical properties of W.[5–8] On the one hand, alloying small amount of element Zr that can bond with oxygen will increase grain boundary strength.[5,6] The incorporation of zirconium by spark plasma sintering in a range of 0.2 wt%–1.0 wt%, with and without additional yttrium oxide (Y2O3) dispersion, have been recently investigated by Liu et al.[5] The results showed that the ductile-brittle transition temperature (DBTT) of W with the addition of 0.2% Zr alone was about 200 °C lower than that of pure W, and ultimate tensile strength was improved by incorporating the Y2O3 particles, which also results in a slight decrease in corresponding ductility. Meanwhile, Xie et al. showed that Zr, decomposed from ZrH2, could capture impurity oxygen in tungsten and form nano-sized monoclinic ZrO2 particles.[6] The tungsten sample with 0.2 wt% ZrH2 addition exhibits not only the highest fracture strength but also the highest toughness. However, the greater than 0.2 wt%-ZrH2 addition leads to the increase of the particle size of dispersoids and the decrease of the fracture strength and toughness.[6] On the other hand, doping ZrC can improve the mechanical properties of tungsten through refining grain size and inhibiting recrystallization.[1] Xie et al. reported that the trace nano-sized ZrC particles were added into W matrix by powder metallurgical process.[8] Both the ductility and strength are significantly improved in comparison with the commercial bulk pure W or W alloy, which can be attributed to coherent interface in grain/phase boundaries tuned by the purifying and strengthening abilities of the trace ZrC.[8] The first-principles calculations indicate that Zr element prefers to occupy the substitutional site in W with negative solution energy, suggesting that Zr element is easily dissolved in tungsten.[9–11] However, there have been few systematic studies of the properties for W–Zr alloy with different Zr concentrations and theoretical research is still required. The advent of density functional theory (DFT) has provided an alternative means of including the electron correlation to seek an insight into the mechanical mechanism.

Experimental results indicate that at room temperature and ambient pressure, W possesses a body-centered cubic (bcc) structure with a lattice constant of 3.165 Å (α phase). In the presence of oxygen, the W has a bcc structure with a lattice constant of 5.046 Å (β phase). However, the β phase transforms into the α phase when the temperature is higher than 630 °C and the process is irreversible. W as a plasma facing material withstand extremely high temperature. Thus, in this work, using the density functional theory, the effects of alloying Zr on the fundamental mechanical properties of W with α phase are studied. The structural, mechanical and electronic properties of W1−xZrx (x = 0.0625, 0.125, 0.1875, 0.25, 0.5) are calculated for different compositions. With the optimized geometry and lattice, some mechanical parameters such as bulk modulus (B), shear modulus (G), Youngʼs modulus (E), Poissonʼs ratio (υ), the B/G ratio, and Cauchy pressure ( ) are derived. In addition, we present our analysis of the electronic properties to explain the mechanism involved in the improvement of the ductility properties of the W–Zr alloy. We anticipate that the obtained results are of significance for theoretically understanding the mechanical properties of W alloying with Zr.

2. Computational methods

First-principles calculations were performed with the pseudopotential plane-wave method implemented in the Vienna ab initio simulation package (VASP) code based on density functional theory (DFT).[12–14] The projector augment wave (PAW)[15] method was used to describe the core orbital, and the electron exchange correlation functional was calculated by using the Perdew–Burke–Ernzerhof approximation (PBE) described by the generalized gradient approximation (GGA).[16] The systematic calculations presented here have been performed on 2×2×2 supercell containing 16 atoms in a body centered cubic structure in W. Previous studies with first-principles calculations have shown that Zr atom can dissolve into bcc W to form substitutional binary solid solution.[17,18] In supercell calculations, the W alloying with different Zr concentrations, where W atoms are progressively replaced by Zr atoms have been studied. Six different Zr concentrations: no substitution (x = 0.0), one W atom replaced by one Zr atom (x = 0.0625), two W atoms replaced by two Zr atoms (x = 0.125), three W atoms replaced by three Zr atoms (x = 0.1875), four W atoms replaced by four Zr atoms (x = 0.25), eight W atoms replaced by eight Zr atoms (x = 0.5), have been performed for calculations. All possible configurations for each composition were here considered. The electron wave function was expanded in plane waves up to a cutoff energy of 350 eV. The calculated equilibrium lattice constant of pure W was 3.19 Å, and the result was consistent with the experimental value of 3.165 Å.[19] The Brillouin-zone integration was performed within Monkhorst–Pack scheme by using a 11×11×11 mesh for the geometry optimization and 13×13×13 mesh for electronic calculation.[20] For the case of pure Zr, the calculations have been performed on 2×2×2 supercell containing 16 atoms in a hexagonal close packing (hcp) structure and the 6×6×4 Monkhorst–Pack mesh has been used. Both supercell size and atomic positions were relaxed to equilibrium, and energy minimization continues until the forces on all atoms are converged to a value smaller than 10−2 eV/Å. The total energy of each system was relaxed until the difference value is smaller than 10−5 V.

We calculated the Cij components of the elastic tensor under the zero pressure from the computation of the stress–strain relationships.[21] According to Hookeʼs law, the stress–strain relationships can be described as Within the framework of the continuum elasticity theory, for the cubic structure, there were three independent elastic constants, i.e., C11, C12, and C44, to describe the response of a crystal to any applied stress.[22] Consequently, the elastic constants for W1−xZrx compounds can be calculated from three different strains as follows: The mechanical properties can be calculated from these single crystal elastic constants, according to the Voigt–Reuss–Hill scheme.[23–26] The bulk modulus (B), shear modulus (G), Youngʼs modulus (E), Poissonʼs ratio (υ), and Cauchy pressure ( ) of W alloying with Zr were derived from C11, C12, and C44 via the following formula:

3. Results and discussion
3.1. Mechanical properties of bcc crystal of tungsten (W)

To check the accuracy of this computational setup, we calculate the single-crystal elastic constants and mechanical property parameters of pure W. The elastic constants and mechanical property parameters are given in Tables 1 and 2, where they are also compared with existing experimental data[27]and previous theoretical investigations performed with first-principles calculations.[28] As evident, the elastic constants and the mechanical parameters of the bcc W, calculated from this work are basically in agreement with the experimental and theoretical results within an expected accuracy of ± 10% for the experimental values. Note that the Perdew–Burke–Ernzerhof approximation that we used in this study is a major source of error. As Momida et al.[30] mentioned, the Perdew–Burke–Ernzerhof approximation, because of its weaker energy-volume dependence, leads to overestimation in calculating the structure geometry and then transfers this error to the calculation of the elastic constants. All in all, our computational setup is reasonable, which illustrates that the calculated elastic properties of W alloying with Zr in the following are reliable.

Table 1.

Elastic constants of bcc W.

.
Table 2.

Bulk modulus (B), shear modulus (G), Youngʼs modulus (E), B/G ratio, Poissonʼs ratio (υ), Cauchy pressure of bcc W and Zr.

.
3.2. Lattice constants and thermodynamic stability

The energy minimization procedure is used to obtain the total energy and optimal atomic relaxation geometries of all possible atomic configurations of W alloying with different Zr concentrations. The energy minimization shows that the W–Zr alloys can keep the bcc lattice and the most stable site for Zr atoms is located at the positions of the configurations in a high-symmetry. These results indicate that the W–Zr binary solid solution can be formed at an atomic level. The schematic diagrams of these high-symmetry configurations are illustrated in Fig. 1, where small purple and large yellow balls represent W and Zr atoms, respectively. Note that the atomic configurations with the lowest energy are selected for subsequent calculations.

Fig. 1. Schematic representation of energetically the most favorable atomic arrangements of the bcc W1−xZrx (x = 0.0625, 0.125, 0.25 and 0.5) in a 2×2×2 supercell. Small purple and large yellow balls represent W and Zr atoms, respectively.

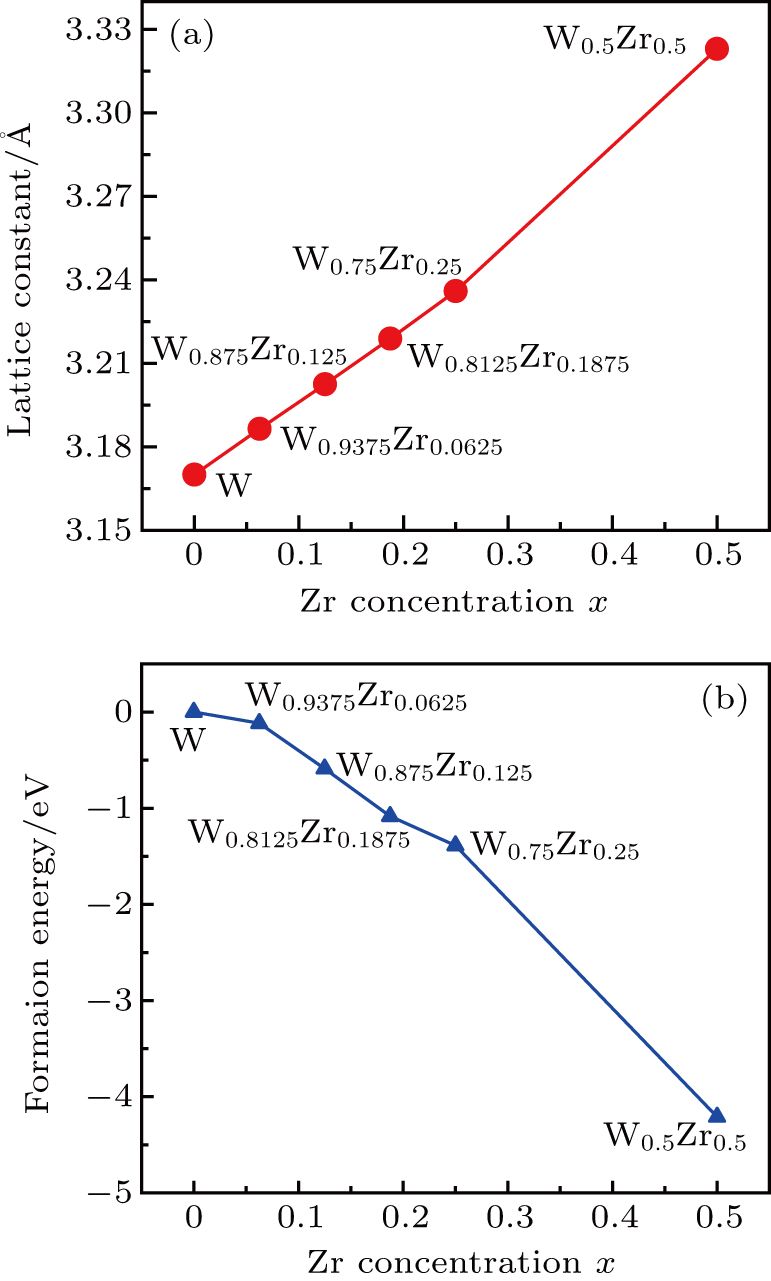The lattice parameters of mixed crystals often obey the Vegardʼs law,[31,32] i.e., the lattice parameter of solid solution is linearly dependent on the concentration of one component and this is valid particularly for substitutional solid solutions.[33] Our calculations for the equilibrium lattice constants of W1−xZrx obtained from the total energy as a function of the volume are shown in Fig. 2(a). As can be clearly seen from Fig. 2(a), the lattice constants of W1−xZrx increase almost monotonically with the Zr concentration increasing, suggesting that the lattice parameters of W1−xZrx obey the Vegardʼs law. This further proves that the W–Zr binary substitutional solid solution can be formed at an atom level, which will be proposed later. In addition, the lattice constants of W1−xZrx are lager than that of pure W, owing to the fact that the radius of the Zr atom is larger than that of the W atom.

Fig. 2. Plots of (a) equilibrium lattice constants and (b) formation energy of bcc W alloying with Zr versus Zr concentration.

A negative formation energy means that a structure is thermodynamically stable.[34–36] The effect of Zr concentration on the thermodynamic stability of W1−xZrx structure is evaluated from formation energy (Ef), which is defined as In this formula, , EW, ans EZr express the total energy of supercells W1−xZrx, supercells W, and supercells Zr, respectively. The x represents the concentration of the Zr element in W–Zr alloy. The calculated results are given in Table 3. Meanwhile, the formation energy values of W1−xZrx as a function of Zr concentration are shown in Fig. 2(b), from which we can know that the formation energy values of W1−xZrx are negative, indicating that the W1−xZrx structures are thermodynamically stable. Moreover, the formation energy values of W1−xZrx decrease with the Zr concentration increasing. These results strongly suggest that the W–Zr binary substitutional solid solution formation is favored.

Table 3.

Cell volumes, elastic constants, and formation energy of bcc W1−xZrx

.
3.3. Mechanical properties

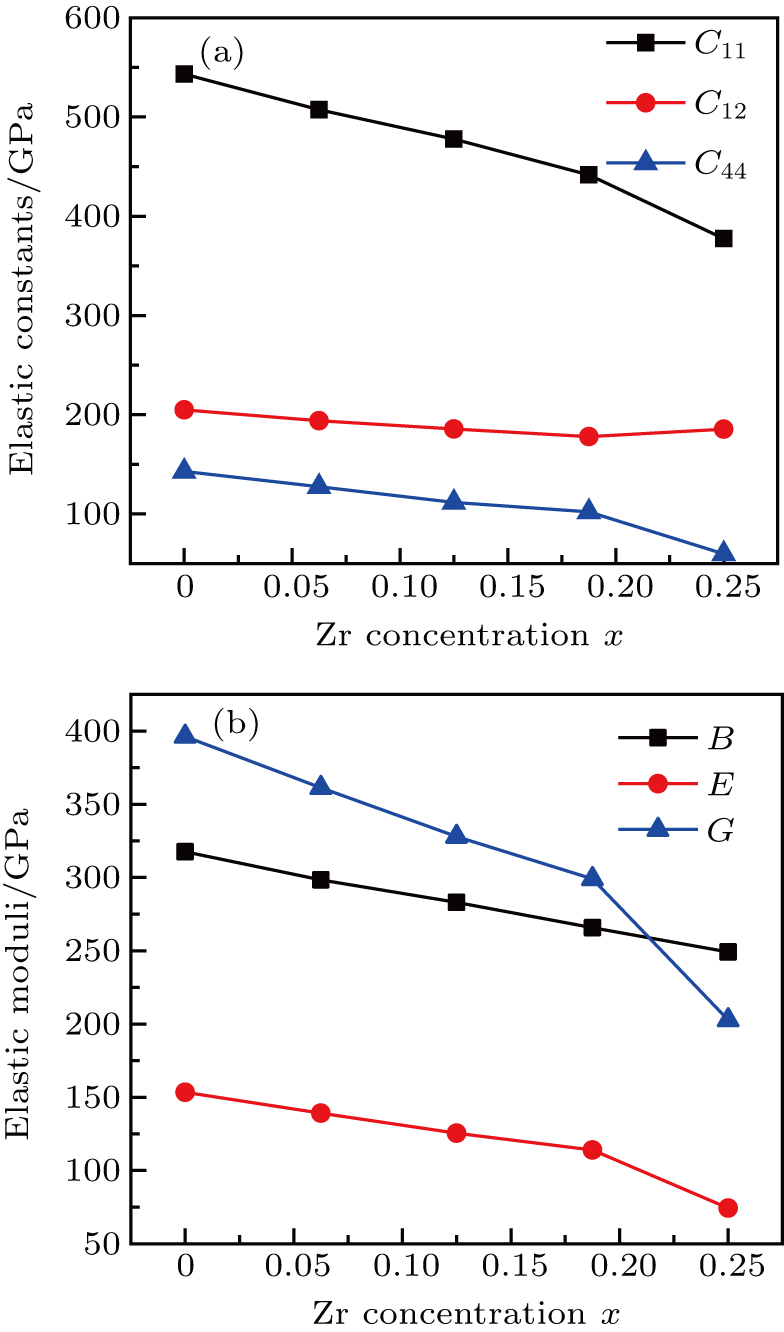
Now, we come to analyze the effect of an increased concentration of Zr on the elastic properties of the W1−xZrx solid solution. The calculated elastic constants relative to those of the pure W as a function of concentration x are given in Table 3 and shown in Fig. 3(a). The stability criteria for cubic crystals are the Born–Huang elastic stability criteria,[37] which are as follows:

Fig. 3. (a) Elastic constants of bcc W alloying with Zr varying with Zr concentration; (b) Bulk modulus (B), shear modulus (G), and Youngʼs modulus (E) of bcc W alloying with Zr varying with Zr concentration.

Our first-principles calculations explicitly indicate that the calculated elastic constants fulfill the above elastic stability criteria. The elastic stability of bcc W1−xZrx solid solution is guaranteed, thus ensuring a mechanically stable model of binary alloy systems. Interestingly, the C11 and C44 are clearly observed to decrease systematically (almost linearly), and the C12 varies with x slightly and nonlinearly. Indeed, the values of C11 reflects the stiffness of cubic crystal. The C11 value changes from 543.28 GPa for pure W to 245.98 GPa for W0.5Zr0.5, demonstrating that the stiffness decreases with the Zr content increasing by 6.25 at.%, until it reaches 50 at.%. In other words, the main elastic constants of the system decrease with Zr concentration, which makes the system softer.

To further understand the macroscopic mechanical properties of W1−xZrx, the values of derived bulk modulus (B), shear modulus (G), Youngʼs modulus (E), the ratio B/G, Poissonʼs ratio (υ), and Cauchy pressure ( ) are summarized in Table 4. The calculations overestimate the bulk modulus by roughly 1% for pure W, and this is within the usual error of the DFT. As we have pointed out above, the results of elastic properties are reliable. The bulk modulus B in transition metal tends to decrease with formation energy decreasing.[38] As can be seen in Figs. 2(b) and 3(b), this rule is also applicable for W–Zr alloys. It is worth noting that the bulk modulus Bdecreases monotonically with the increase of Zr concentration. The W alloying with Zr will reduce the bulk modulus in comparison with that of pure tungsten. When Zr concentration reaches 18.75%, the bulk modulus of W–Zr alloy decreases to 265.83 GPa. Hence, the resistance to deformation of tungsten will be reduced by alloying with Zr. A similar behavior is also shown in the variation trend of shear modulus and Youngʼs modulus. As a consequence of this trend, the W–Zr alloys with higher Zr concentration become softer than pure W metal. However, they are much more rigid than pure Zr metal.[39]

Table 4.

Values of bulk modulus (B), shear modulus (G), Youngʼs modulus (E), B/G ratio, Poissonʼs ratio (υ), Cauchy pressure for bcc W alloying with Zr

.

The ratio of the bulk over shear modulus, B/G, has been proposed by Pugh[37] to identify a brittle or ductile behavior of the material. According to the Pugh criterion, a high B/G value (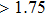 ) indicates a tendency for ductility; otherwise, the material behaves in a brittle manner. The B/G ratio as a function of Zr concentration x for the bcc W alloying with Zr and for pure W are presented in Fig. 4(a). As revealed by Fig. 4(a), all the values of B/G are high than 1.75, implying that the W–Zr alloys are ductile materials in nature. Meanwhile, with the increase of Zr concentration, the B/G value increases gradually. When the Zr concentration reaches 18.75%, the B/G value is 2.33 larger than that of pure W (2.07). It is suggested that doping Zr can improve the ductility of bcc W. In addition, Frantsevich et al.[40] devised a rule on the basis of Poissonʼs ratio (υ) to make a distinction between ductile and brittle material. For the criterion, the critical value of υ is 0.26.[41] Moreover, the larger υ value, the better ductility a material possesses. The values of Poissonʼs ratio in our calculations are more than 0.26 for W–Zr alloys, indicating a rather ductile character of these materials in the same way as B/G ratio does. As shown in Fig. 4(a), the variation of the Poissonʼs ratio with Zr concentration exhibits a similar trend to that of the B/G ratio. When the Zr concentration reaches 18.75%, the Poissonʼs ratio is 0.312 larger than the Poissonʼs ratio that the pure W has (0.29). The same conclusion for the estimation of ductility can be obtained from analyzing the υ value.

Fig. 4. Plots of (a) B/G ratio and Poissonʼs ratio and (b) Cauchy pressure ( ) versus Zr concentration for bcc W alloying with Zr.

According to the analyses in the relevant research papers, the intermetallic compound of W2Zr is formed very easily when the temperature reaches a value between 1400 °C and 2210 °C, which will lead to the brittleness damage to W based materials. The intermetallic compound of W2Zr phase has a body-centered cubic structure and the phase prototype is W. Thus, the ductility of W2Zr phase should be improved based on our first-principles calculation. Noting that the data obtained by using first-principles simulation have limitations and in particular the effect of temperature on the data needs to be carefully assessed. Thus, the effects of temperature on W–Zr alloy and the properties of intermetallic compound of W2Zr will be studied in our future work.

The angular characteristic of atomic bonding, which also relates to the brittle/ductile properties of metals and metallic compounds, could be described by the Cauchy pressure.[42] For directional bonding with angular characteristic, the Cauchy pressure is typically negative. Meanwhile, for metallic bonding, the Cauchy pressure is positive, with larger positive pressure representing a more metallic characteristic and the better ductility. 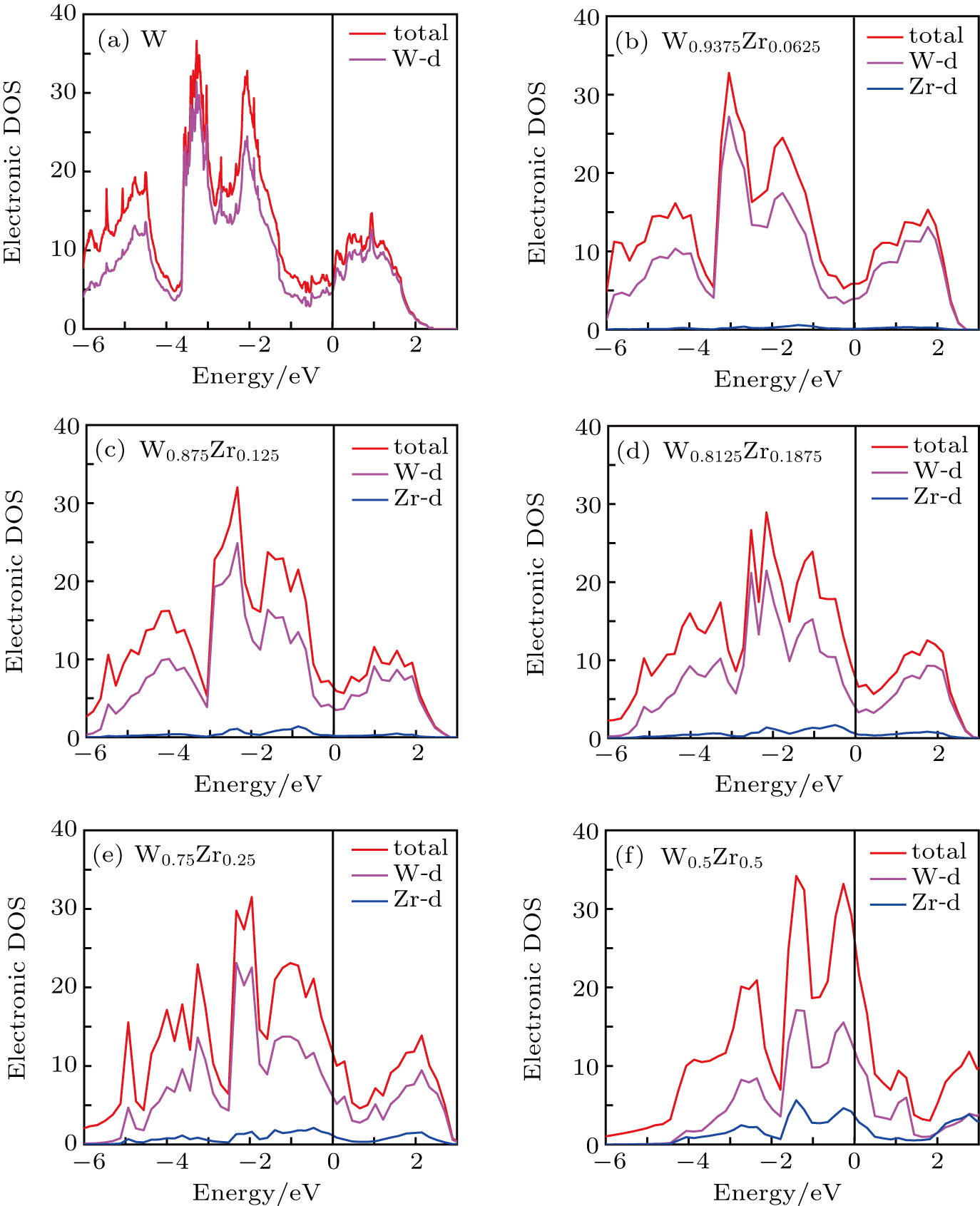As shown in Table 4, the Cauchy pressures are positive for all the bulk W–Zr alloys, clearly indicating metallic bonding is predominant. A positive value of calculated Cauchy pressure, in addition to reflecting their metallic characteristic, indicates their ductile nature. Furthermore, with the increase of Zr concentration, the B/G value increases gradually, which suggests that the metallic bonding is strengthened by alloying Zr in the bcc bulk W.

3.4. Electronic structures

To understand the mechanical properties of W–Zr alloys, their underlying electronic structures are analyzed. Figure 5 shows the calculated total and partial densities of states (TDOS and PDOS) for W–Zr alloys under various compositions. As displayed in Fig. 5, there is no energy gap at Fermi level for W–Zr alloys, meaning that all these compounds present metallic character. The main bonding peaks of W–Zr alloys are located near the Fermi level in a range from −6 eV to 3 eV, which mainly originate from the contribution of the 5d orbital of W and Zr. With Zr content increasing, the peaks of W atom lower their heights while the peak height of Zr atom rises. Meanwhile, the Fermi level moves away from the minimum of the TDOS to the left peak, suggesting that bonding in the alloys becomes more metallic.[43] This is consistent with the above analysis of Cauchy pressure. Moreover, Söderlind et al.ʼs study shows that the shapes of the DOS do not depend on the kind of the element but on the crystal structure.[44] This tendency of the DOS is applicable not only for pure metals but also for binary alloys.[45] figure 5 obviously shows that the quantity of the Zr elements does not seem to affect the shape of DOS but only moves Fermi level, implying that the W–Zr alloys have the same bcc structure as the pure W except for the lattice constant.

Fig. 5. Density of states (DOS) of bcc-based chemically random W1−xZrx: (a) W when x = 1, (b) W0.9375Zr0.0625, (c) W0.875Zr0.125, (d) W0.8125Zr0.1875, (e) W0.75Zr0.25, (f) W0.5Zr0.5, with energy being relative to Fermi level.
4. Conclusions

The structural, mechanical and electronic properties of W1−xZrx (x = 0.0625, 0.125, 0.1875, 0.25, 0.5) binary bcc substitutional alloys are systematically investigated by means of first-principles calculations within the framework of DFT. The formation energy values of all the studies W1−xZrx alloys are negative, indicating that they are all energy thermodynamically stable. Based on the calculations of the elastic constants, all the bcc W1−xZrx structures satisfy the mechanical stability criteria, i.e., the W–Zr binary substitutional solid solution can be formed at an atom level. Moreover, the elastic constants and the elastic moduli of W–Zr alloys are found to decrease gradually with the increase of Zr concentration, implying that the W–Zr alloys with higher Zr concentration become softer than pure W metal, although it is more rigid than the pure Zr metal. Meanwhile, by analyzing the value of B/G ratio, Poissonʼs ratio υ and Cauchy pressure , we demonstrate that all the W1−xZrx alloys are ductile materials, and increasing the Zr concentration in tungsten is helpful in improving the ductility. The calculated density of states suggests that the bcc structure W1−xZrx is metallic and the bonding in the alloys becomes more metallic with the increase of Zr concentration in tungsten. This explains the mechanism for the improvement of ductility properties of W–Zr alloys. The effects of alloying Zr on important properties of W, such as the thermal conductivity, hydrogen retention, helium retention, etc., will be studied in our future work.

Reference
[1] Ren C Fang Z Z Koopman M Butler B Paramore J Middlemas S 2018 Int. J. Reercat. Met. H. 75 170
[2] Barabash V Federici G Matera R Raffray A R ITER Home Teams 1999 Phys. Scr. T81 74
[3] Federici G Anderl R A Andrew P ITER Home Teams 1999 J. Nucl. Mater. 266�?69 14
[4] Federici G Wuerz H Janeschitz G Tivey R 2002 Fusion Eng. 61�?2 81
[5] Liu R Xie Z Hao T Zhou Y Wang X Fang Q Liu C 2014 J. Nucl. Mater. 451 35
[6] Xie Z Liu R Fang Q Zhou Y Wang X Liu C 2014 J. Nucl. Mater. 444 175
[7] Xie Z Liu R Zhang T Fang Q Liu C Liu X Luo G 2016 Mater. Des. 107 144
[8] Xie Z Liu R Miao S Yang X Zhang T Wang X Fang Q Liu C Luo G Lian Y Liu X 2015 Sci. Rep. 5 16014
[9] Wu X Kong X S You Y W Liu C S Fang Q F Chen J L Luo G N Wang Z 2014 J. Nucl. Mater. 455 151
[10] Wu X Kong X S You Y W Liu C S Fang Q F Chen J L Luo G N Wang Z 2013 Nucl. Fusion 53 073049
[11] Kong X S Wu X B You Y W Liu C S Fang Q F Chen J L Luo G N Wang Z G 2014 Acta Mater. 66 172
[12] Kresse G Furthmüller J 1996 Phys. Rev. 54 11169
[13] Kresse G Furthmüller J 1996 Comput. Mater. Sci. 6 15
[14] Kresse G Joubert D 1999 Phys. Rev. 59 1758
[15] Blöchl P E 1994 Phys. Rev. 50 17953
[16] Perdew J P Burke K Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
[17] Hu Y J Fellinger M R Bulter B G Wang Y Darling K A Kecskes L Kecskes L J Trinkle D R Liu Z K 2017 Acta Mater. 141 304
[18] Wu X Kong X S You Y W Liu C S Fang Q F Chen J L Luo G N Wang Z G 2013 Nucl. Fusion. 53 073049
[19] Rasch K D Siegel R W Schultz H 1980 Philos. Mag. 41 91
[20] Monkhorst H J Pack J D 1976 Phys. Rev. 13 5188
[21] Zhao J J Winey J M Gupta Y M 2007 Phys. Rev. 75 094105
[22] Wallace D C 1970 Solid State Phys. 25 301
[23] Voigt W 1889 Ann. Phys. 274 573
[24] Reuss A 1929 Zamm-Z Angew Math. Mech. 9 49
[25] Hill R 1963 J. Mech. Phys. Solids 11 357
[26] Zhai D Wei Z Feng Z F Shao X H Zhang P 2014 Acta Phys. Sin. 63 206501 in Chinese
[27] Soderlind P Eriksson O Wills J Boring A 1993 Phys. Rev. 48 5844
[28] Einarsdotter K Sadigh B Grimvall G Ozolins V 1997 Phys. Rev. Lett. 79 2073
[29] Liu W Li B S Wang L P Zhang J Z Zhao Y S 2008 Appl. Phys. 104 076102
[30] Momida H Yamashita T Oguchi T 2014 J. Phys. Soc. Jpn. 83 124713
[31] Vegard L 1921 Z. Phys. 5 17
[32] Wei Z Zhai D Shao X H Zhang P 2015 Chin. Phys. 24 043102
[33] Hotje U Rose C Binnewies M 2003 Solid State Sci. 5 1259
[34] Jiang D Y Ouyang C Y Liu S Q 2016 Fusion Eng. 106 34
[35] Jiang D Zhou Q Xue L Wang T Hu J F 2018 Fusion Eng. 130 56
[36] Wei X Chen Z Zhong J Wang L Wang Y P Shu Z L 2018 J. Magn. Mater. 456 150
[37] Li C M Hu Q M Yang R Johansson B Vitos L 2010 Phys. Rev. 82 094201
[38] Zhu L F Friák M Dick A Grabowski B Hickel T Liot F Holec D Schlieter A Kühn U Eckert J Ebrahimi Z Emmerich H Neugebauer J 2012 Acta Mater. 60 1594
[39] Pugh S F 1954 London Edinburgh Dublin Philos. Mag. J. Sci. 45 823
[40] Yoo H M Takasugi T Hanada S Izumi O 1990 Mater. Trans. JIM 31 435
[41] Kamran S Chen K Y Chen L 2009 Phys. Rev. 79 024106
[42] Söderlind P Eriksson O Wills J M Boring A M 1993 Phys. Rev. 48 5844
[43] Wei N Jia T Zhang X Liu T Zeng Z Yang X Y 2014 AIP Adv. 4 057103
[44] Ikehata H Nagasako N Furuta T Fukumoto A Miwa K Saito T 2004 Phys. Rev. 70 174113
[45] Turchi P E A Gonis A 2001 Phys. Rev. 64 085112