Unlike conventional imaging that is based on the first-order correlation of light, correlated imaging concepts including auto-correlation imaging schemes^[1–4] and ghost imaging schemes^[5–13] employ the second-order correlation of light. It results in some unique features and has attracted a lot of attention in last decades. In fact, correlated imaging has been applied in various fields including optical lithography,^{[14, 15]} remote imaging,^[16] microscopy imaging,^[17] x-ray imaging,^[18] and Terahertz imaging.^[19]

In these applications, the spatial resolution of image is a major issue. In conventional imaging, the resolution is given by Rayleigh criterion^[20] which comes from the finite-size of the entrance pupil of the imaging system. In auto-correlation imaging, the resolution is determined by the product of the point spread functions (PSFs) of the two light beams.^[1–4] In ghost imaging, the resolution is in general quantified by the full width at half-maximum (FWHM) of the peak in a Hanbury-Brown and Twiss (HBT) intensity correlation measurement, or by use of the transverse coherence length of the illumination speckles, namely the averaged size of the speckles.^{[1, 21–23]} In the last decade, a great deal of resolution enhancement proposals have been suggested, such as compressive sensing technique^[24–26] and non-Rayleigh speckle fields,^{[27, 28]} low-pass spatial filter scheme,^[23] and high-pass spatial-frequency filter scheme.^[29] In a recent publication, Yang et al.^[30] reported a new correlated imaging scheme using the orbital angular momentum correlations of light. This scheme may be used to image an object with a very high azimuthal resolution. Although those investigations to the resolution of ghost imaging have been done, to our knowledge, how the optical systems in the test and the reference path of ghost imaging individually affect the imaging resolution is not clear. Is the resolution of ghost imaging also given by the product of the two light beamʼs PSFs as in auto-correlation imaging?

In this work, a Gaussian-shaped spot illumination scheme is employed to analyze the resolution issue of ghost imaging. We demonstrate that the resolution of ghost imaging is determined by the convolution of the PSFs of the test and reference light beams. Then, we propose localization and threshold methods to diminish the effect of the PSFs and enhance the resolution of ghost imaging. In photo-activated localization microscopy (PALM) scheme,^[31] a sub-diffraction image is constructed by localizing the positions of the fluorophores.^{[31, 32]} In our scheme, we show that by localizing the central positions of all the illuminated spots of the reference light beam, the resolution of ghost imaging can be enhanced by a factor of . We also find that the resolution can be further enhanced by setting an appropriate threshold to the bucket measurement.^[33–35]

A typical ghost imaging schematic is shown in Fig. 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic diagram of the ghost imaging. An illumination light is split into two paths by a 50:50 beam splitter. In the test path, the light illuminates the object and then is collected by a bucket detector with no spatial resolution. In the reference path, the light intensity distribution is recorded by a charge-coupled device (CCD) camera.

Suppose that the light beam in the test path propagates to the object through an optical system with a PSF . Here and are the transverse coordinates on the source and the object plane, respectively. If represents the transmission function of the object, the light field behind the object is given by

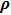
Suppose that the PSF of the reference path is . The optical field on the charge-coupled device (CCD) plane is given by

If the light source is in a Gaussian-type quantum state, the second-order correlation of the bucket signals and the reference signals can be written as^[13]

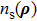
In order to explicitly analyze spatial resolution of ghost imaging, we consider the case where the illumination light is a point-like source which randomly and uniformly distributed on the source plane. If the light spot is located at , we may have , where is a constant. In this case, we have

As is well known, the image in a conventional imaging system can be expressed in the form^[36]

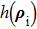
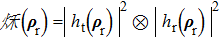
In order to work out an explicit expression of the resolution of ghost imaging, we assume that all the PSFs in Eqs. (6) and (7) have the same Gaussian form . Inserting the PSF into Eqs. (6) and (7), we obtain the formula for ghost imaging

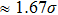
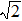
As shown in Eqs. (6) and (8), the object transmission function is related to the correlation function by the convolution with the PSFs of the test and reference paths. Thus, either performing deconvolution algorithms or implementing deconvolution processes, one may extract the higher resolution image from the correlation function. In the following, we introduce two deconvolution methods: localizing and thresholding.

For this end, as similar as in the localization process,^[31] we precisely label central positions of light spots of each illumination pattern in the reference light beam. In mathematics, it means that the PSF of the reference beam in Eq. (6) is replaced by a δ-function .^{[31, 32]} In this way, equation (6) can be simplified as

Here, in order to understand how the PSFs affect the resolution, we study the case where the object is a pinhole at . As shown in Fig. 2(a), a set of Gaussian-shaped spots are shining on the object, and for each spot, only the light intensity at is recorded as the bucket value. The distribution of the corresponding bucket detection values is shown as the color circles on the red solid curve in Fig. 2(a) with respect of the relative positions of the light spots. According to the ghost imaging protocol, the correlations are reconstructed by multiplying the corresponding light spots in the reference path with the bucket detection values, shown as the dashed color curves in Fig. 2(b). Thus, the conventional ghost image of the pinhole, shown as the blue curve in Fig. 2(b), is the convolution of the reference light spots with the distribution of the bucket detection values as illustrated in Eq. (6), in which the FWHM quantifies the resolution of ghost imaging and shows wider than that of the Gaussian illumination spots. Note that the image is given by the convolution but not the simple multiplies of the light spots with the corresponding bucket detection values. That is why the FWHM of light spots in the reference arm affects the resolution of ghost imaging. Now, it becomes clear that one can get an image of the pinhole with smaller size if the FWHM of the spots in the reference arm is reduced. In the limit case where the spot in the reference arm is reduced to a point, the image is given by the distribution of the bucket detection values. It is the usual Airy disk, shown as the black solid curve in Fig. 2(c). Thus, the resolution of ghost imaging can be enhanced by a factor of if the light spot has a Gaussian shape and the light spot in the reference arm is reduced to a point as illustrated in Eq. (10).

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. (a) A pinhole object located at is illuminated by single Gaussian-shaped spots with different central locations. The colors indicate the positions of the Gaussian spots. The circles on the red solid curve indicate the distribution of the bucket measurement values. (b) Conventional ghost image of the pinhole reconstructed from the overlaps of the multiplies of the reference Gaussian envelops with the corresponding bucket values. (c) Localized ghost image of the pinhole. Each reference Gaussian envelop in (b) is replaced by its central point. The red solid curve indicates a threshold to the bucket measurement.

Then we choose the post-selection method^[35] to diminish the effect of the PSF of the test path. With this method, only the bucket measurement values larger than a threshold are reserved and others are abandoned. If the maximal value of the bucket measurement is I_max and the threshold is set to be I_th, as shown in Fig. 2(c), the effective FWHM labeled by the red double-arrowed lines is given by

Next, to increase the signal strength of the bucket detector and improve the anti-noise ability of the imaging system, the multi-spot illumination scheme is the most commonly used in ghost imaging.^[37–43] If each illumination pattern contains M light spots, based on the theory developed in the preceding section, we can drive out the imaging formula

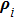
The first term is the desired image and the second one is the background noise resulting from cross talks between different illumination spots. It is clear that the localizing and thresholding methods proposed in the preceding section for resolution enhancement can be used to the multi-spot illumination case if central positions of all spots in an illumination pattern are recorded prior to the illumination.

The experimental setup is shown in Fig. 3. A light beam from a He-Ne laser with wavelength λ=632.8 nm passes through the beam expander and arrives at the Spatial Light Modulator (SLM, RSLM1024U, Shanghai Realic Information Technology Corporation, Ltd). The SLM is codified by a computer to generate the transverse patterns with random distribution of light spots. After the SLM, the light passes through a 4f-system and then it is demagnified by a factor of 6. The group 4, element 4 portion of the resolution chart (Thorlabs negative USAF1951), which consists of triple alternating stripes with the separation of , is taken as an object. The transmitted light of the object is collected by a bucket detector. In this scheme, the computer-programming patterns are recorded prior to the correlation measurement and the computational ghost imaging protocol is implemented.^{[44, 45]}

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. Experimental setup of computational ghost imaging. The beam expander is used to expand the transverse section of the light beam from the laser source. The Spatial Light Modulator (SLM) is controlled by a computer to generate illumination patterns of light spots with random central positions. After demagnified by the 4f-system, the light spots illuminate the object (group 4, element 4 portion of USAF resolution chart), and the transmitted light is collected by a bucket detector.

In experiment, the FWHM of the Gaussian-shaped spot shinning the object plane varies from to , and to . The sampling frames used to construct the ghost image is 5×10⁵. As indicated in Eq. (6), the maximal FWHM of the spots which can distinguish the strips is , because is close to the separation of the stripes. When the FWHM takes the critical value, the result is shown in Fig. 4(a) and the stripes are not very clear. In Figs. 4(b) and 4(c), we observe that the images become further blurred and indistinguishable with increasing the FWHM values. The ghost images with the localization method are shown in Figs. 4(d)–4(f). In constructing the images, we use a Gaussian-shaped light spot with 12- FWHM as the light spots of the reference beam. The resolution enhancement is obvious and the images become clearer not only with the FWHM but also with which is larger than the separation of the strips.

Fig. 4.

Figure Option ViewDownloadNew Window

Fig. 4. The images obtained from the ghost imaging experimental setup described in Fig. 1. From left to right column images, the FWHM of the light spots is , , and , respectively. (a)–(c) The results from the conventional ghost imaging; (d)–(f) from the ghost imaging with the localization method; (g)–(i) with the localization and threshold methods by setting ; (j)–(l) the corresponding cross-sectional images. The blue, black and red profiles stand for the results from the conventional ghost images, the ghost imaging with the localization method and the localized ghost imaging with the threshold selection, respectively. The unit a.u. is short for arbitrary units.

To further raise the resolution, we set a threshold to the bucket measurement. It means that only the values of the bucket measurement larger than the threshold are used to construct the images. The results are shown in Figs. 4(g)–4(i). By comparing Figs. 4(g)–4(i) with Figs. 4(d)–4(f), we observe that the resolution is further enhanced. However, when illuminating with the light spots of FWHM , it is hard to say the strips becomes distinguishable because the image is distorted as shown in Fig. 4(i).

In Fig. 5, the experimental results of multi-spot illumination case are shown. In comparison with Fig. 4, the images will sacrifice the image visibility a little since the background is introduced in. But one may use light spots with low intensity and obtain high bucket detection signals in the multi-spot illumination case.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The ghost imaging experimental results achieved with 5-spot illumination in each pattern. The FWHM of the light spots is . Panel (a) is the same as Fig. 4(a); (b) the same as Fig. 4(d); (c) the same as Fig. 4(g); (d) the corresponding cross-sectional images. The set is the same as Fig. 4(g). Here, the background is approximately eliminated with correlation formula .

Finally, we would like to emphasize two points. At first, the threshold method may also be suitable to a gray-scale object although the binary object is used in the present demonstration. For a gray-scaled object, light spots shinning on the low gray-scale regions would be abandoned if the threshold is set too high, and the contrast resolution would be decreased and the image get distorted. For a gray-scaled object, one should appropriately divide the object into several zones according to its gray distribution and set different threshold values for different zones. Then, the ghost imaging process is performed zone-by-zone and the whole image of the object can be constructed by combining the images of the different zones. It means that for a gray-scale object one should dynamically set a threshold value to the bucket measurement. Secondly, the localization and threshold methods also can be implemented when the light source of ghost imaging is not point-like and not Gaussian shape. In that case, Gaussian-distributed fit allows the reference pattern transform to be the overlaps of the Gaussian spots and the central positions of the spots also can be tracked.^{[32, 46]} Therefore, the two methods to enhance the resolution are applicable to any other ghost imaging protocols.

In this work, we sequentially analyzed the diffraction effects of the test and reference paths, and individual contributions to the spatial resolution of ghost imaging are quantified. Next, we showed that the PSF of the reference path can be removed by localizing central positions of the reference patterns and the image resolution can be enhanced by a factor of . In addition, the influence from the PSF of the test path can be diminished by setting an appropriate threshold to the bucket measurement and the resolution can be further enhanced. We experimentally demonstrated the resolution enhancement in both single-spot and multi-spot illumination schemes, and the results are well in agreement with the theoretical prediction. Except the resolution improvement, the experimental results in Fig. 4 show a superior visibility and signal-to-noise ratio, and thus our scheme deserves to be applied in current available technology.