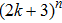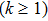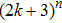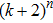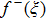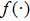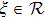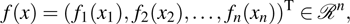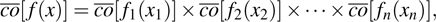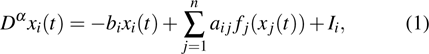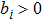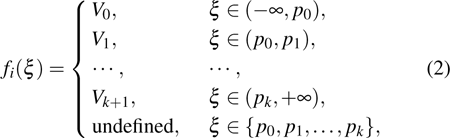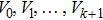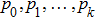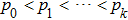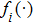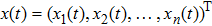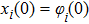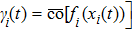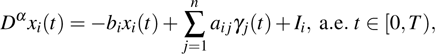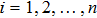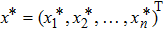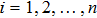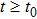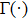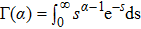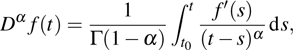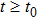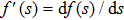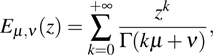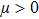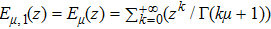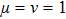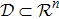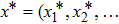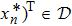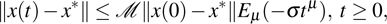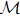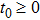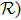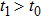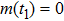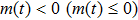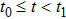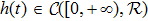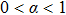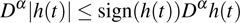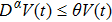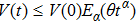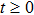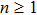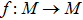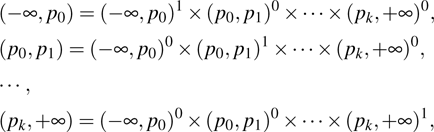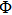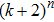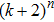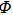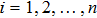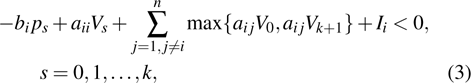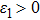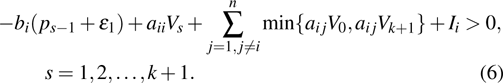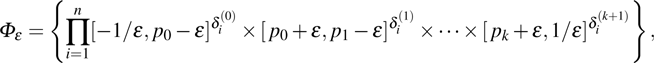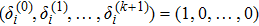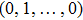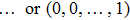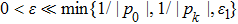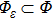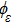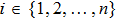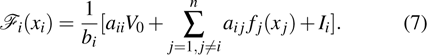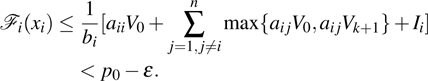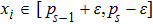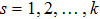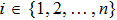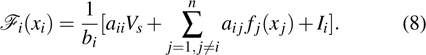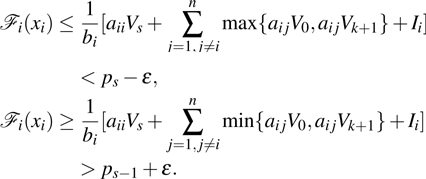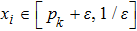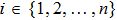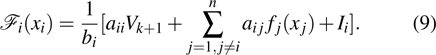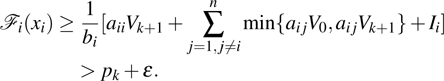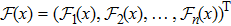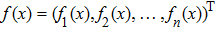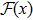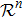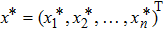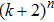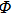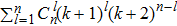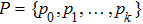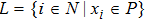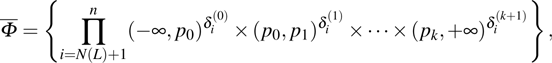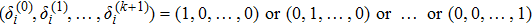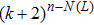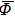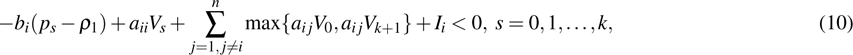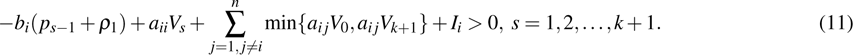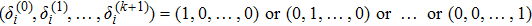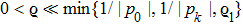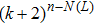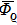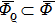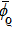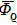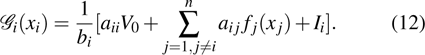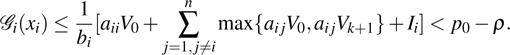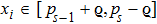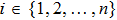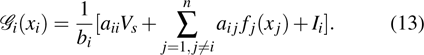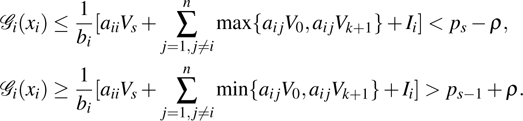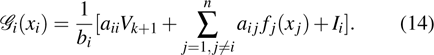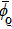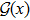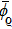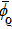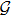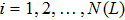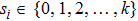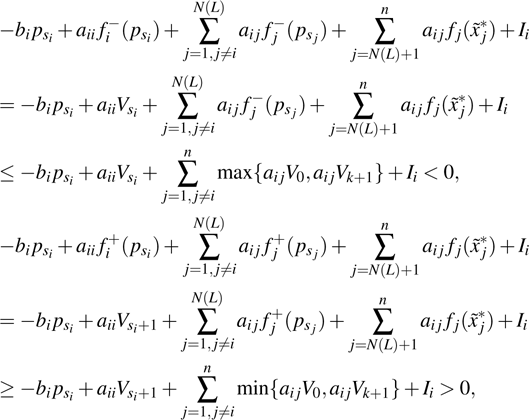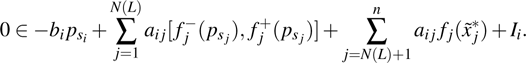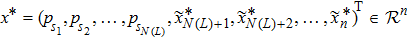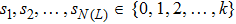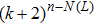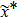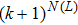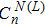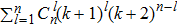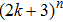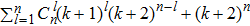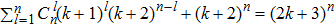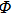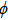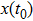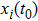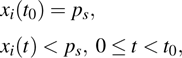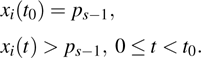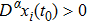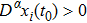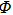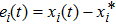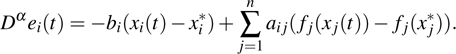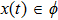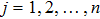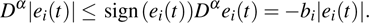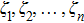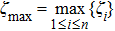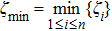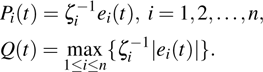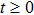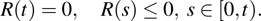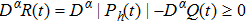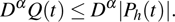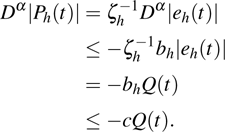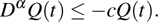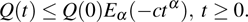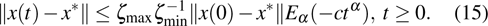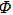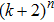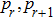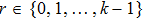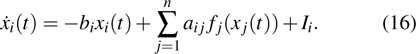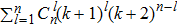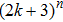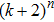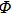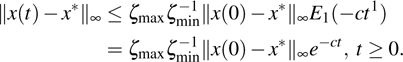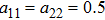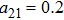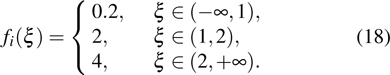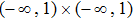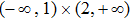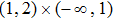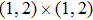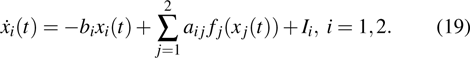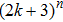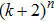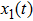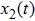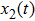Coexistence and local Mittag–Leffler stability of fractional-order recurrent neural networks with discontinuous activation functions
1. IntroductionDue to the wide applications in many fields, such as pattern recognition, associative memory, signal processing, optimization, and many other fields, artificial neural networks have been investigated in depth in recent decades.[1–5] Some applications, such as optimization, require network to have only one equilibrium point which is monostable. However, the multiple/stable equilibrium points of neural networks are demanded in some other applications such as associative memory and pattern recognition. The property that a neural network has multiple stable equilibrium points is called multistability of the neural network. When the neural network is applied for associative memory, the basic premise is to make sure that the neural network has a large number of stable equilibrium points. Therefore, the main purpose of investigating multistability of neural networks is to increase the number of stable equilibrium points.[6] Some considerable efforts have been devoted to investigating the issue. Multistability of two kinds of recurrent neural networks with activation functions symmetrical about the origin on the phase plane was investigated in [7]. Multiple μ-stability of neural networks with unbounded time-varying delays was considered in [8]. Multistability of recurrent neural networks with nonmonotonic activation functions and unbounded time-varying delays was discussed in [9]. Multistability in Mittag–Leffler sense of fractional-order neural networks with piecewise constant arguments was addressed in [10]. Many other works on multistability of recurrent neural networks can be found in [11–15] and the references cited therein.
Fractional-order calculus which deals with derivatives and integrals in the form of noninteger order was established more than 300 years ago. Compared with the integer-order theory, the developments in the fractional-order theory have been rather slow. Lately, there has been a steady growth of interest in the fractional-order theory because lots of actual systems show fractional-order differential dynamical behaviors. A great number of applications about fractional-order derivative system have been found in science and engineering, such as drug absorption and disposition processes,[16] electromagnetic waves,[17] fractional damped oscillators and fractional forced oscillators,[18] viscoelastic systems,[19] heat conduction,[20] neural networks,[21] and so on. Noting that fractional calculus provides a powerful tool for describing memory and hereditary properties of systems.[22] So fractional-order derivative has been incorporated into neural networks. Meanwhile, fractional-order parameter can increase the flexibility of system parameter selection by introducing one more degree of freedom.[21] Fractional-order neural networks might be expected to play an important role in parameter estimation. Hence, the incorporation of memory term (a fractional derivative or integral) into neural network models is an extremely important improvement.[23] It is also necessary to study the fractional-order neural networks.
In recent years, dynamical behaviors of fractional-order recurrent neural networks have been investigated. α-stability and α-synchronization of fractional-order neural networks were presented in [24]. The authors discussed global Mittag–Leffler stability and synchronization of memristor-based fractional-order neural networks in [25]. The authors studied uniform stability of fractional-order complex-valued neural networks with time delays in [26]. The Mittag–Leffler stability and asymptotical ω-periodicity of fractional-order fuzzy neural networks were considered in [27]. The multiple Mittag–Leffler stability of fractional-order recurrent neural networks was investigated in [28]. An LMI-based uniform stability condition of fractional-order neural networks with time delay was established in [29]. Many other valuable works on dynamic analysis of fractional-order neural networks can be found in [23] and [30–34] and the references cited therein.
It is well known that the activation functions play an important role in the dynamical analysis of recurrent neural networks. The storage capacity of pattern recognition and associative memory rely heavily on the structures of activation functions. As mentioned in [35], a brief overview on some common neural network models reveals that neural networks described by differential equations with a discontinuous right-hand side are of importance and do frequently arise in practice. When dealing with dynamical systems possessing high-slope nonlinear elements, it is often advantageous to model them with a system of differential equations with discontinuous right-hand side. Much efforts have been devoted to analyzing the dynamical properties of neural networks with discontinuous activation functions in [36–38] and the references therein. There are also plenty of valuable works addressing the multistability issue of recurrent neural networks with discontinuous activation functions.[6,39–41] However, to the best of our knowledge, most results concentrate upon the multistability of integral-order neural networks with discontinuous activation functions, and there are few results on the multistability of fractional-order ones with discontinuous activation functions. As a result, it is necessary to investigate the multistability of fractional-order neural networks with discontinuous activation functions.
Motivated by the above discussions, the purpose of this paper is to explore the coexistence and multiple Mittag–Leffler stability of fractional-order recurrent neural networks with discontinuous activation functions. The main contributions of this paper can be listed as follows:
(i) Based on the decomposition of state space, sufficient conditions are established for the existence of
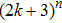 equilibrium points. Due to the incorporation of discontinuous activation functions, the neural networks might have higher storage capacity than the continuous ones.
equilibrium points. Due to the incorporation of discontinuous activation functions, the neural networks might have higher storage capacity than the continuous ones.
(ii) By using the results in fractional-order derivative, sufficient conditions are established to ensure local Mittag–Leffler stability of
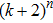 equilibrium points. The speed of convergence in Mittag–Leffler sense is fast.
equilibrium points. The speed of convergence in Mittag–Leffler sense is fast.
(iii) The results of fractional-order recurrent neural networks with discontinuous activation functions are extended to those of integral-order recurrent neural networks. Sufficient conditions are established to ensure coexistence and local exponential stability of integral-order recurrent neural networks.
The remainder parts of this paper consist of the following sections. Section 2 describes some preliminaries and problem formulations. The main results are stated in Section 3. Two examples are used to show the effectiveness of the obtained results in Section 4. Finally, the conclusion is drawn in Section 5.
Notations: The notation used in this paper is fairly standard.
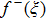 and
and
 denote, respectively, the left and the right limits of function
denote, respectively, the left and the right limits of function
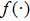 at point
at point
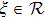 .
.
 is the closure of the convex hull for set M. For a vector-valued function
is the closure of the convex hull for set M. For a vector-valued function
define
where

for

and ‘×’ represents the Cartesian product.
2. Preliminaries and problem formulationsIn this section, we present the neural network model discussed in this paper, and then give a brief introduction of the properties of fractional-order calculus, which includes the definitions and some useful lemmas.
Consider the following fractional-order recurrent neural networks:
where

,
α is the order of fractional-order differential equation (
1) with


represents the state of the
i-th neuron at time
t;
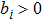
is the self-regulating parameter of the neuron;
aij is the connection weight of the
j-th unit on the
i-th unit;

is the activation function;
Ii represents the external input. We consider a general class of discontinuous activation function as follows:
where
 k
k is an integer that satisfies

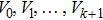
,
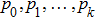
are constants with

,
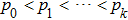
. Typical configuration of the activation function is depicted in Fig.
1.
Since
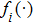 is allowed to have points of discontinuity, we need to specify what mean by solution of the system having a discontinuous right-side. For this purpose, we consider the solution of fractional-order recurrent neural networks (1) in the sense of Filippov.[42]
is allowed to have points of discontinuity, we need to specify what mean by solution of the system having a discontinuous right-side. For this purpose, we consider the solution of fractional-order recurrent neural networks (1) in the sense of Filippov.[42]
Definition 1[36] For a given constant vector
 , the absolute continuous function x(t) with
, the absolute continuous function x(t) with
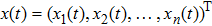 and
and
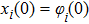 is said to be a solution of system (1) on [0,T) if there exist measurable functions
is said to be a solution of system (1) on [0,T) if there exist measurable functions
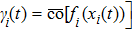 for almost all
for almost all
 such that
such that
where
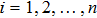
.
Definition 2[36] The point
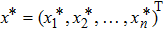 is said to be an equilibrium point of system (1) if
is said to be an equilibrium point of system (1) if
hold for all
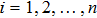
.
Definition 3[43] The fractional integral of order α for a function f is defined as
where
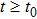
and

,
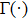
is the Gamma function, that is
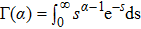
.
Definition 4[43] Let f(t) is a differentiable function on
 , the Caputo fractional derivation of order α of f(t) is defined by
, the Caputo fractional derivation of order α of f(t) is defined by
where
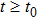
,

, and
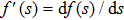
.
Definition 5[43] A two-parameter Mittag–Leffler function is defined by
where
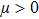
,
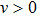
, and

. If

, then
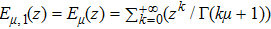
. If
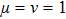
, then

.
Definition 6 Suppose
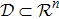 is a positive invariant set,
is a positive invariant set,
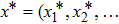 ,
,
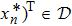 is an equilibrium point of system (1). The equilibrium point
is an equilibrium point of system (1). The equilibrium point
 is locally Mittag–Leffler stable, if for any
is locally Mittag–Leffler stable, if for any
 , x(t) of system (1) satisfies
, x(t) of system (1) satisfies
where
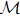
,
μ and
σ are positive constants.
Lemma 1[28] Assume that
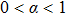 ,
,
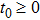 , and
, and
 ,
,
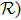 is differentiable. If there exists
is differentiable. If there exists
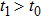 such that
such that
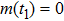 and
and
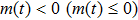 for
for
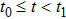 , then
, then
 .
.
Lemma 2[32] If
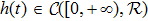 , then for any
, then for any
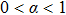
holds almost everywhere.
Lemma 3[25] If
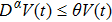 almost everywhere for
almost everywhere for
 , then
, then
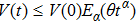 for
for
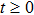 , where θ is a constant.
, where θ is a constant.
Lemma 4 (Brouwerʼs fixed point theory[44]) Suppose that M is a nonempty, convex, compact subset of
 , where
, where
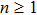 , and that
, and that
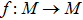 is a continuous mapping. Then f has a fixed point.
is a continuous mapping. Then f has a fixed point.
For the convenience of description, make some denotations as follows:
and denote
where

or

or

. It is easy to see there exist

subregions in
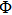
. In the next section, we will investigate the existence and stability of the equilibrium point in every subregion of

.
3. Main resultsIn this section, we will discuss the existence and stability for fractional-order recurrent neural networks with discontinuous activation functions. Some sufficient conditions will be established to ensure system (1) with activation function (2) can have
 equilibrium points, among which
equilibrium points, among which
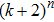 equilibrium points are locally Mittag–Leffler stable. Moreover, conditions for the existence and stability of equilibrium points for integral-order recurrent neural networks will be derived. The main results are stated one by one as follows. Firstly, we will discuss the existence of equilibrium points for system (1) with the characteristic that all the components of equilibrium points are in the continuous regions of activation function (2).
equilibrium points are locally Mittag–Leffler stable. Moreover, conditions for the existence and stability of equilibrium points for integral-order recurrent neural networks will be derived. The main results are stated one by one as follows. Firstly, we will discuss the existence of equilibrium points for system (1) with the characteristic that all the components of equilibrium points are in the continuous regions of activation function (2).
Theorem 1 There exist
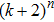 equilibrium points in
equilibrium points in
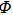 for system (1) with activation function (2) if the following conditions hold for
for system (1) with activation function (2) if the following conditions hold for
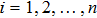
Proof From conditions (3) and (4), there exists a small enough
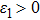 such that
such that
Make some denotations as follows:
and denote
where
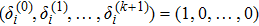
or
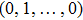
or
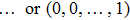
,
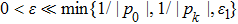
. It is easy to see there exist

subregions in

, and
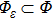
. Let
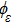
be an arbitrary subregion located in

. There exist the following three cases to discuss.
Case 1
When
 ,
,
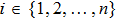 , denote
, denote
It can be derived from condition (
5) that
Case 2
When
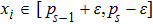 ,
,
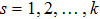 ,
,
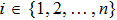 , denote
, denote
It can be derived from conditions (
5) and (
6) that
Case 3
When
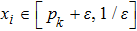 ,
,
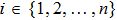 , denote
, denote
It can be derived from condition (
6) that
Denote
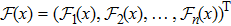 , where
, where
 are defined in expressions (7), (8), (9), respectively. Because
are defined in expressions (7), (8), (9), respectively. Because
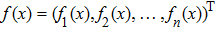 is a continuous function in region
is a continuous function in region
 ,
,
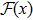 is a continuous function in region
is a continuous function in region
 . Meanwhile
. Meanwhile
 is a nonempty, convex, compact subset of
is a nonempty, convex, compact subset of
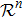 .
.
 is mapping the points in
is mapping the points in
 onto itself. Based on Brouwerʼs fixed point theorem, there exists a fixed point
onto itself. Based on Brouwerʼs fixed point theorem, there exists a fixed point
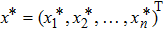 such that
such that
 . It is easy to see that
. It is easy to see that
 is the equilibrium point of system (1). As a result of arbitrariness of
is the equilibrium point of system (1). As a result of arbitrariness of
 , there exists
, there exists
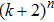 equilibrium points in
equilibrium points in
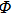 for system (1) with activation function (2).
for system (1) with activation function (2).
Next, we will discuss the existence of equilibrium points for system (1) with the characteristic that some components of equilibrium points are just the discontinuous points of activation function (2).
Theorem 2 If conditions (3) and (4) hold, system (1) with activation function (2) has
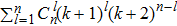 equilibrium points with the characteristic that some components of them are just the discontinuous points of the activation function (2).
equilibrium points with the characteristic that some components of them are just the discontinuous points of the activation function (2).
Proof Define
 ,
,
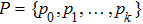 ,
,
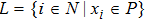 . Let N(L) be the number of elements in L. Without loss of generality, suppose that
. Let N(L) be the number of elements in L. Without loss of generality, suppose that
 ,
,
 . Denote
. Denote
where
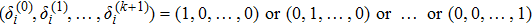
. Then there exist
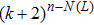
subregions in
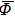
. From conditions (
3) and (
4), there exists a small enough

such that
Make some denotations as follows:
and denote
where
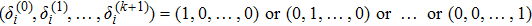
,
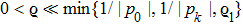
. It is easy to see there exist
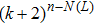
subregions in
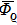
, and
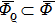
. Let
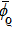
be an arbitrary subregion located in
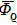
. There exist the following three cases to be discussed below.
Case 1
When
 ,
,
 , denote
, denote
It can be derived from condition (
10) that
Case 2
When
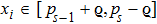 ,
,
 ,
,
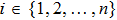 , denote
, denote
It can be derived from conditions (
10) and (
11) that
Case 3
When
 ,
,
 , denote
, denote
It can be derived from condition (
11) that
Denote
 , where
, where
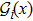 are defined in Eqs. (12), (13), (14), respectively. Because
are defined in Eqs. (12), (13), (14), respectively. Because
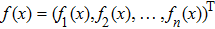 is a continuous function in region
is a continuous function in region
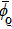 ,
,
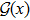 is a continuous function in region
is a continuous function in region
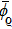 . Meanwhile
. Meanwhile
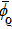 is a nonempty, convex, compact subset of
is a nonempty, convex, compact subset of
 .
.
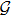 is mapping the points in
is mapping the points in
 onto itself. Based on Brouwerʼs fixed point theorem, then there exists one fixed point
onto itself. Based on Brouwerʼs fixed point theorem, then there exists one fixed point
 such that
such that
 .
.
On the other hand, for
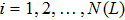 ,
,
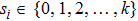 , we can gain from conditions (3) and (4) that
, we can gain from conditions (3) and (4) that
which infer that
Therefore,
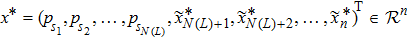 is an equilibrium point for system (1) with
is an equilibrium point for system (1) with
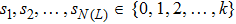 . By arbitrariness of
. By arbitrariness of
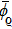 , there are
, there are
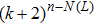 fixed points
fixed points
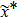 such that
such that
 . Meanwhile, there are k+1 discontinuous points for activation function (2). So there are
. Meanwhile, there are k+1 discontinuous points for activation function (2). So there are
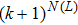 cases in which some components of
cases in which some components of
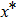 are just the discontinuous points in activation function (2). Moreover, there are
are just the discontinuous points in activation function (2). Moreover, there are
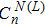 cases to choose
cases to choose
 components which are just the discontinuous points. It follows that there are
components which are just the discontinuous points. It follows that there are
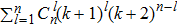 equilibrium points for system (1) with activation function (2).
equilibrium points for system (1) with activation function (2).
According to Theorem 1 and Theorem 2, we can obtain the following result.
Theorem 3 If the conditions (3) and (4) hold, there exist
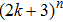 equilibrium points for the system (1) with activation function (2).
equilibrium points for the system (1) with activation function (2).
Proof Integrated Theorem 1 and Theorem 2, there exist
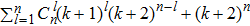 equilibrium points for the system (1) with activation function (2). According to Newtonʼs binomial theorem, we can obtain that
equilibrium points for the system (1) with activation function (2). According to Newtonʼs binomial theorem, we can obtain that
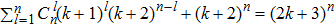 . This completes the proof.
. This completes the proof.
Remark 1 Due to the incorporation of discontinuous activation functions, the neural networks might have higher storage capacity than the continuous ones.
In order to investigate the stability of equilibrium points of system (1) with activation function (2), it is necessary to discuss the invariance of the region
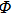 .
.
Lemma 5 Suppose conditions (3) and (4) hold. The region
 is positively invariant.
is positively invariant.
Proof Let
 be an arbitrary subregion located in
be an arbitrary subregion located in
 . We claim that the solution x(t) of system (1) will stay in
. We claim that the solution x(t) of system (1) will stay in
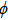 for all
for all
 . If this is not true, there exists some time
. If this is not true, there exists some time
 such that
such that
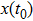 escapes from ϕ. Without loss of generality, suppose that
escapes from ϕ. Without loss of generality, suppose that
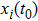 escapes from
escapes from
 ,
,
 ,
,
 . Then it follows that
. Then it follows that
or
For the first case, we can obtain
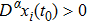
from Lemma 1. From conditions (
3) and (
4), it holds that
This yields a contradiction to
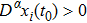 . Similarly, the second case is either not true. Therefore, x(t) will stay in ϕ for all
. Similarly, the second case is either not true. Therefore, x(t) will stay in ϕ for all
 . That is,
. That is,
 is positively invariant.
is positively invariant.

Next, we will investigate the stability of the equilibrium points in
 for system (1) with activation function (2).
for system (1) with activation function (2).
Theorem 4 If conditions (3) and (4) hold, there exist
 local Mittag–Leffler stable equilibrium points in
local Mittag–Leffler stable equilibrium points in
 for system (1) with activation function (2).
for system (1) with activation function (2).
Proof According to Theorem 1, there are
 equilibrium points for system (1) with activation function (2) in
equilibrium points for system (1) with activation function (2) in
 . Now we will discuss the stability of these equilibrium points. Let ϕ be an arbitrary subregion located in
. Now we will discuss the stability of these equilibrium points. Let ϕ be an arbitrary subregion located in
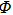 .
.
 is the equilibrium point located in ϕ.
is the equilibrium point located in ϕ.
Let
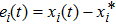 , then
, then
When
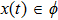
,

,
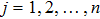
. So,
According to Lemma 2
Choose some positive constants
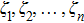
. Let
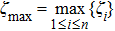
,
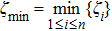
. Define
For any
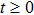
, there exists

such that
Let

, then we have
According to Lemma 1,
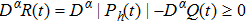
, which implies that
Meanwhile we can obtain
where

,

. Hence,
According to Lemma 3
On the other hand
Obviously
Therefore, the equilibrium point

located in
ϕ is locally Mittag–Leffler stable. Due to the arbitrary of the picked subset
ϕ,
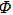
have

regions like subset
ϕ. Hence, there exist

local Mittag–Leffler stable equilibrium points for system (
1) with activation function (
2).
Remark 2 Fractional-order neural networks have infinite memory and more degrees of freedom. As a result of these rewards, the fractional-order model is more accurate than the corresponding integer-order model, and they have more complicated properties. Moreover, the methods which are commonly utilized in multistability analysis of integer-order neural networks could not be directly extended to multistability analysis of fractional-order ones. To this end, Lemmas 1–3 are introduced in this paper.
Remark 3 Based on the configuration of activation function (2), the space
 can contain
can contain
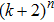 parts. Each of these parts is an attractive basin of one stable equilibrium point. If the length of any one section (for example (
parts. Each of these parts is an attractive basin of one stable equilibrium point. If the length of any one section (for example (
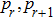 ),
),
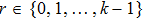 ) in activation function (2) increases, then the attractive basin of the corresponding equilibrium point will be increased. We can gain that the attractive basins of equilibrium points rely heavily on the configuration of activation functions.
) in activation function (2) increases, then the attractive basin of the corresponding equilibrium point will be increased. We can gain that the attractive basins of equilibrium points rely heavily on the configuration of activation functions.
Remark 4 In [28], the multiple Mittag–Leffler stability of fractional-order recurrent neural networks has been investigated. The activation functions were required to be continuous, whereas for the discontinuous activation functions, the obtained results cannot be utilized.
It is worth noting that the above results can be generated in the following integral-order recurrent neural networks
The activation function

is described as in activation function (
2). According to the similar discussion of the above results, we can obtain the following corollaries.
Corollary 1 Suppose that conditions (3) and (4) hold. There exist
 equilibrium points in
equilibrium points in
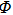 for system (16) with activation function (2).
for system (16) with activation function (2).
Corollary 2 If conditions (3) and (4) hold, the system (16) with activation function (2) has
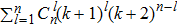 equilibrium points with the characteristic that some components of them are just the discontinuous points of the activation function (2).
equilibrium points with the characteristic that some components of them are just the discontinuous points of the activation function (2).
Corollary 3 If the conditions (3) and (4) hold, there exist
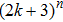 equilibrium points for the system (1) with activation function (2).
equilibrium points for the system (1) with activation function (2).
Corollary 4 Suppose that conditions (3) and (4) hold. There exist
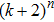 local exponentially stable equilibrium points in
local exponentially stable equilibrium points in
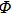 for system (16) with activation function (2).
for system (16) with activation function (2).
Remark 5 Actually, for integral-order recurrent neural networks (16), equation (15) can be rewritten as follows:
Hence, the equilibrium points of system (
16) are locally exponentially stable.
Remark 6 According to Corollaries 1–4, we can gain that Theorem 4 includes the multistability of integer-order neural networks as a special case.
4. Illustrative examples
Example 1
Consider the following two-neuronal fractional-order recurrent neural network:
where
α=0.9,
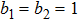
,
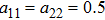
,

,
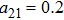
,

. The activation function

are defined as follows:
System (
17) satisfies conditions (
3) and (
4). That is,
According to Theorems 1 and 4, the system (
17) with activation function (
18) has 9 local Mittag–Leffler stable equilibrium points. The dynamics of system (
17) are illustrated in Figs.
2–
4.
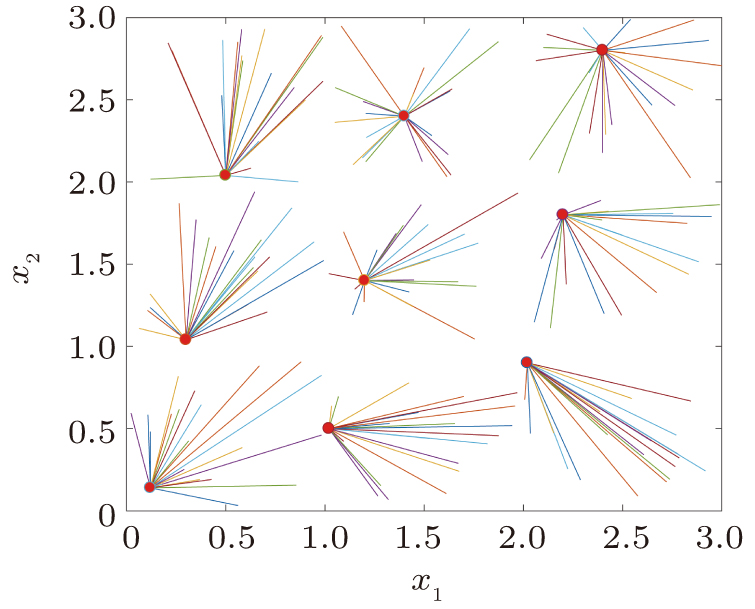
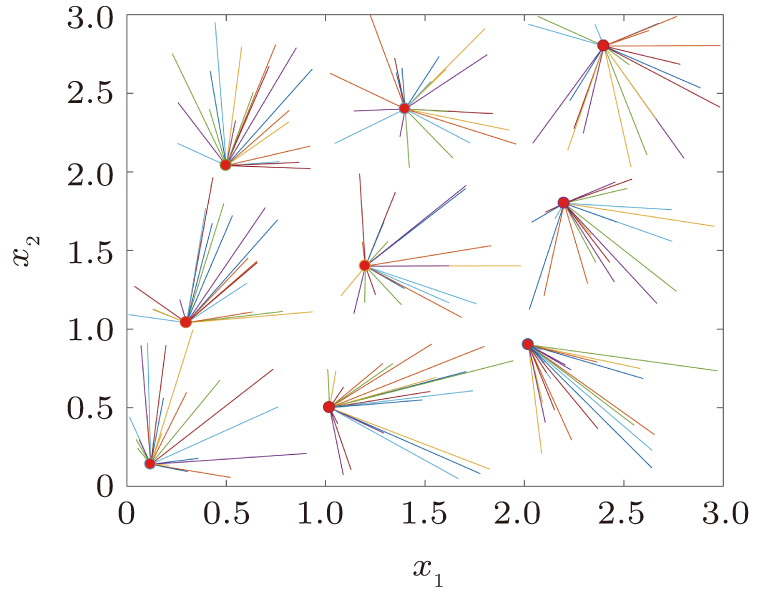
According to Fig. 2, evolutions of 180 initial conditions have been tracked, which converge to 9 stable equilibrium points marked in red. The attractive basins of 9 stable equilibrium points are
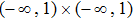 ,
,
 ,
,
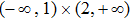 ,
,
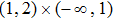 ,
,
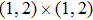 ,
,
 ,
,
 ,
,
 ,
,
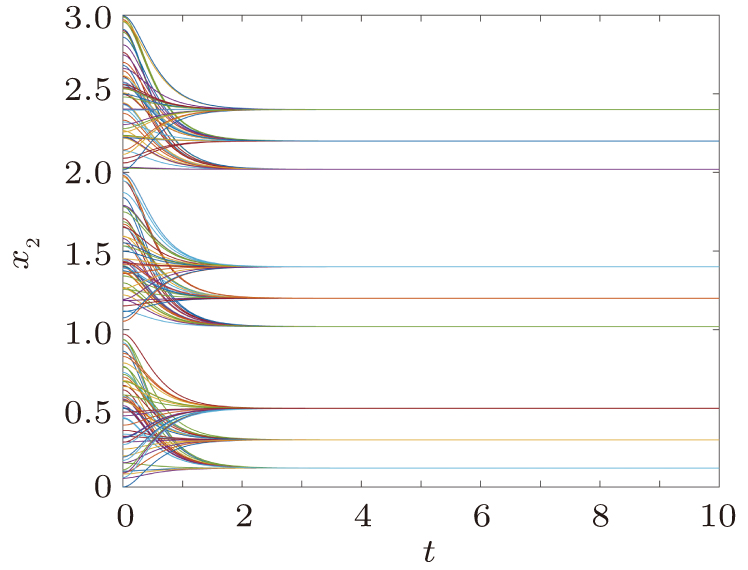
 , respectively. Figure 3 and 4 also display initial conditions of x1 and x2 converge to 9 points. The effectiveness of the theoretical results has been verified.
, respectively. Figure 3 and 4 also display initial conditions of x1 and x2 converge to 9 points. The effectiveness of the theoretical results has been verified.
Example 2
Consider the following 2-neuronal integral-order recurrent neural network:
Parameters are the same as those in Example 1. According to Corollaries 1 and 4, the system (
19) with activation function (
18) has 9 local exponentially stable equilibrium points. The dynamics of the system (
19) are illustrated in Figs.
5–
7. The effectiveness of the theoretical results has been verified.
Remark 7 By calculating, 9 equilibrium points of fractional-order neural network (17) and integral-order neural network (19) are both as follows, (0.12,0.14), (0.3,1.04), (0.5,2.04), (1.02,0.5), (1.2,1.4), (1.4,2.4), (2.02,0.9), (2.2,1.8), (2.4,2.8). It can be seen that derivative of differential equations does not affect the distribution of equilibrium points. The derivative has a certain influence on the speed of convergence.
5. ConclusionIn this paper, multistability has been studied for fractional-order recurrent neural networks with a class of general discontinuous activation functions. It has shown that under some sufficient conditions, the system can have
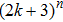 equilibrium points,
equilibrium points,
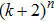 of them are locally Mittag–Leffler stable. The results have been extended to the cases of integer-order recurrent neural networks. By introducing the discontinuous activation functions, the neural networks can have more equilibrium points in the whole state space. The theoretical results and simulations have demonstrated that discontinuous activation functions play an important role in increasing the quantity of equilibrium points of the system. The time delay of neural networks is unavoidable because of the finite speed of a signalʼs switch and transmission. There are few results about multistability of delayed fractional-order differential equations. So our further research work might be multistability of delayed fractional-order recurrent neural networks with discontinuous activation functions.
of them are locally Mittag–Leffler stable. The results have been extended to the cases of integer-order recurrent neural networks. By introducing the discontinuous activation functions, the neural networks can have more equilibrium points in the whole state space. The theoretical results and simulations have demonstrated that discontinuous activation functions play an important role in increasing the quantity of equilibrium points of the system. The time delay of neural networks is unavoidable because of the finite speed of a signalʼs switch and transmission. There are few results about multistability of delayed fractional-order differential equations. So our further research work might be multistability of delayed fractional-order recurrent neural networks with discontinuous activation functions.