† Corresponding author. E-mail:
In this paper, we propose a novel quantum secret image-sharing scheme which constructs m quantum secret images into m+1 quantum share images. A chaotic image generated by the logistic map is utilized to assist in the construction of quantum share images first. The chaotic image and secret images are expressed as quantum image representation by using the novel enhanced quantum representation. To enhance the confidentiality, quantum secret images are scrambled into disordered images through the Arnold transform. Then the quantum share images are constructed by performing a series of quantum swap operations and quantum controlled-NOT operations. Because all quantum operations are invertible, the original quantum secret images can be reconstructed by performing a series of inverse operations. Theoretical analysis and numerical simulation proved both the security and low computational complexity of the scheme, which has outperformed its classical counterparts. It also provides quantum circuits for sharing and recovery processes.
Recent years have witnessed a rapid development in information technology. However, security problems of digital images are a major problem in transmitting vital images. A large number of real-time image processing tasks have brought new challenges to classical computers. Fortunately, quantum computation[1] brings hope for traditional information processing. A quantum computer has been demonstrated to have bright prospects as compared with the classical computer, particular with respect to Feynmanʼs computation model,[2] Shorʼs integer factoring algorithm,[3] and Groverʼs database searching algorithm.[4]
With the development of quantum computation, an emerging branch, i.e., quantum image processing (QIP)[5,6] is attracting more and more attention. It focuses on extending classical image processing tasks and operations to the quantum computation framework. Available literature on QIP can be classified into two groups. In the first, methods to represent quantum images have been proposed, such as a flexible representation of quantum images,[7] a novel enhanced quantum representation (NEQR) of the digital image model,[8] and a normal arbitrary quantum superposition state.[9] In the second, QIP algorithms have been investigated, such as quantum image scaling,[10,11] quantum image matching,[12,13] quantum image steganography,[14–16] and quantum image watermarking.[17–20] In particular, quantum image encryption[21–24] has begun to draw increasing attention in recent years. For example, in [21], a novel image encryption scheme based on quantum walks was proposed, which opens the door towards introducing quantum computation into image encryption. In [22], a novel quantum grayscale image encryption algorithm based on one-dimensional quantum cellular automata was proposed. The proposal has outperformed its classical counterpart in terms of security and computational complexity.
Just as the research on quantum image encryption has become an attractive field, quantum secret sharing,[25–28] which is an important branch of quantum communication,[29] also attracts increasing attention nowadays. From a historical viewpoint, Naor and Shamir[30] presented a visual secret-sharing scheme first which encrypts a secret binary image into n meaningless share images such that the information of the secret image can be decrypted by superimposing all n share images. After that, secret sharing has become a favorite research topic, especially quantum schemes. Theoretically, as a quantum image is still a quantum state, it can also be shared. Quantum secret image sharing, different from traditional secret sharing, is sharing entangled states of a quantum image. To the best of our knowledge, few papers have been published on this issue previously. For example, a novel and flexible quantum image secret-sharing scheme was proposed,[31] which generates shares via measurement operations on the secret image. Two efficient remote medical image-sharing schemes were proposed,[32] which utilize quantum information hiding techniques. Obviously, the research on quantum image sharing is deficient at present. Inspired by the above-mentioned schemes of quantum image processing techniques, this paper mainly focuses on quantum secret image sharing, which constructs m quantum secret images into m+1 quantum share images.
The rest of this paper is organized as follows. Section
The novel enhanced quantum image representation (NEQR) of digital images[8] using two entangled qubit sequences integrates quantum image information, including coordinates position and color information, into a normalized superposition quantum state. For a 

 |
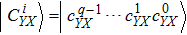
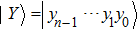
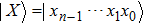
To represent a quantum grayscale image, NEQR needs eight qubits encoding the pixel information, which have 256 grayscale densities. Figure
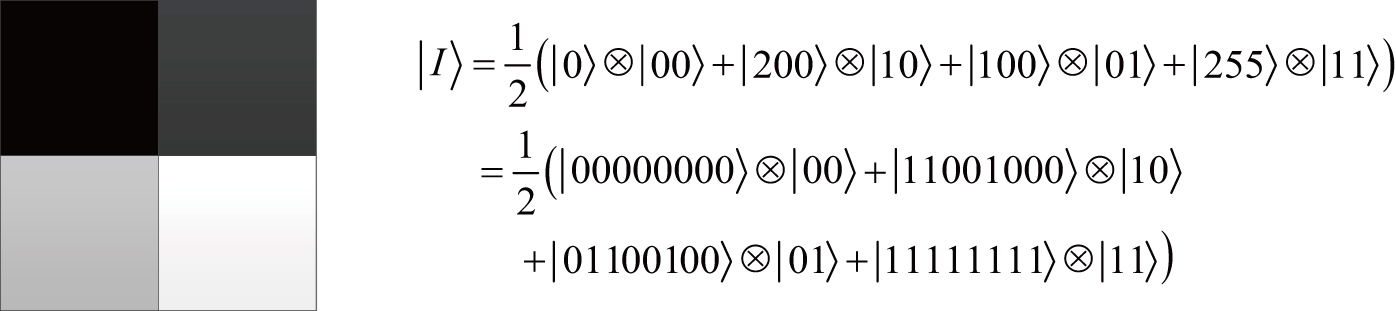 | Fig. 1. 2 × 2 quantum image and its NEQR expression (figure adapted from [8]). |
As a classical algorithm, the logistic map plays an essential role in image encryption because of its high sensitivity to initial conditions, system parameters, and pseudo-random property. In the proposed quantum secret image-sharing scheme, the logistic map is used to generate pseudo-numbers, which are defined as
 |


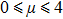
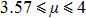
Arnold transform aims to transform an image into a meaningless one through permutation of the positions of the pixels into new positions. Assume that I(X,Y) is an original image with a size of 

 |
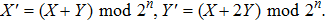
 |
(i) Controlled-NOT operation
In quantum computers, the basic controlled operation is the controlled-NOT (CNOT), which is a quantum gate with two qubits, namely the control qubit and the target qubit (Fig. 

(ii) Quantum swap gate
The quantum swap gate is a two-qubit gate, which can exchange two qubits. The corresponding quantum circuit is shown in Fig.
Zhou et al. designed the quantum equal (QE) circuit for comparing two qubit sequences.[33] The concrete quantum circuit and its simplified module are illustrated in Fig. 






In this section, we will first provide a high-level description of our scheme. The intuition of our scheme using three phases including qubit scrambling, qubit swapping, and the qubit CNOT operation, is to share multiple quantum secret images. In the first phase, the original quantum secret images are scrambled by Arnold transform, which is often used as the image preprocessing method in information hiding. Furthermore, since a grayscale image can be decomposed into eight binary images, a quantum grayscale image also consists of eight binary qubits (i.e., eight qubit planes). To make the shares random, qubit planes are swapped with the participation of the quantum chaos image. Finally, to enhance the security, the quantum CNOT operation is employed, which makes the secret completely random and secure. The process of quantum secret image sharing and recovery is outlined in Fig.
Assume there are m secret images, named I1, I2, …, Im, with the same dimensions 
 |
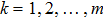
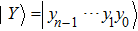
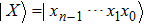
Meanwhile, in the proposed scheme, a meaningless chaotic image created by the logistic map is prepared. For logistic map 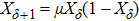




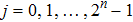
 |
To enhance the confidentiality, the original quantum secret image 
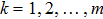



 |
 |
In this process, qubit planes of the scrambled quantum secret images and the quantum chaotic image are swapped in a predefined order. First, the coordinates of the quantum chaotic image 

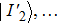













The quantum swapping circuit is illustrated in Fig. 


To obtain the final quantum share images, the quantum controlled-NOT operation (introduced in Subsection 2.4) is utilized to realize a quantum image XOR operation. We define
 |
 |
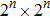
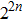
 |
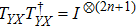
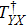
 |
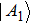
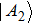
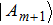
All m+1 quantum share images collected together are used to reconstruct the original quantum secret images. The recovery process consists of four steps.
 |
 |
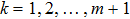




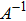

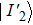










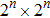
To demonstrate the computation steps in the sharing and recovery processes, we give a trivial example for m = 2. That is, two quantum secret images would be utilized to construct three quantum share images. Assume there are one chaos quantum image (


The pixel values in their qubit form are shown as follows:
 |
 |
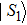
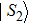
 |
Since all quantum secret images are distinct and the quantum chaotic image is random, the obtained quantum share images are also random and distinct. Thus, 


In summary, compared with the traditional secret image-sharing schemes, which involve complex computation, the proposed scheme constructs the shares only using some basic quantum gate operations. Using quantum parallel processing, the computational efficiency is considerably improved. In addition, the proposed scheme can share m secret images rather than one image only, that is, m quantum secret images can be shared at once by means of sharing m+1 quantum share images. Theoretically, it is simple and efficient.
To demonstrate the feasibility of the proposed scheme, the simulations were conducted using MATLAB 2014b on a classical computer. In the numerical simulations, to generate the chaotic quantum image I0 (Fig. 

 | Fig. 10. (a) Chaotic image, (b) secret image Lena, (c) secret image Peppers, (d)–(f) three share images, and (g)–(h) reconstructed images. |
In this subsection, we analyze the security of the proposed quantum image-sharing scheme from two aspects. On the one hand, we analyze the security issue based on statistical properties. On the other hand, we analyze the security issue based on quantum effects.
First, as we know, the image histogram reflects the pixel distribution of an image. An idea share image should have a uniform frequency distribution. The histograms of the secret images and share images are shown in Fig.
 | Fig. 11. (a)–(b) The histogram of the secret images Lena and Peppers, (c)–(f) the histogram of the three share images. |
Second, since the correlation reflects the degree of similarity of two variables, each pixel in the original image is highly correlated with its adjacent pixels in general. The correlation coefficient R(x,y) of adjacent pixels is simply defined by the following equation:
 |
 | Fig. 12. Distribution of two horizontal direction, vertical direction, and diagonal direction adjacent pixels, (a)–(c) the secret image Lena, (d)–(f) the share image S2. |
| Table 1.
Correlation coefficients of adjacent pixels. . |
In the classical secret image-sharing scheme, the share images are easily affected by different types of noise and known attacks during transmission. It is necessary to discuss the security of the proposed scheme based on quantum effects.[22] As we know, the quantum no-cloning theorem forbids cloning an unknown quantum state accurately. When it is measured, an unknown quantum state will collapse. The no-cloning theorem provides another perspective on the lack of accessibility suffered by quantum information in comparison to classical information. Therefore, the characteristics of quantum mechanics can ensure the security of the proposed scheme to some extent. Although it seems unconditional security can be achieved in quantum communication in theory, when the quantum share images transmit in a practical quantum channel, the quantum states are destroyed by decoherence and quantum noise easily. Some strategies, such as quantum error correction[36] and quantum error rejection,[37,38] can be used in this case. That is, these solutions could be useful for the transmission of quantum share images theoretically. Through this method, the original quantum secret images can be reconstructed even if several qubits are flipped or lost.
The quantum circuit complexity depends on the number of basic quantum gates.[36,39] It has been pointed that one Toffoli gate can be simulated by six CNOT gates and one swap gate can be simulated by three CNOT gates. In this paper, we choose the CNOT gate as the basic unit. The circuit complexity of the n-CNOT (




However, for a classical image with a size of 



We have proposed a novel quantum secret image-sharing scheme which constructs m quantum secret images into m+1 quantum share images. The quantum image-sharing process can be realized by some basic quantum gate operations. Because all quantum operations are invertible, the quantum image recovery process is the inverse of the sharing process. Theoretical analysis and simulation experiments have shown that the proposal has outperformed its classical counterparts in terms of security and computational complexity. Moreover, multiple quantum secret images can be shared simultaneously without involving complex quantum operations, and the proposal is simple and efficient to implement due to quantum parallel processing. In the future, quantum secret image-sharing techniques may be used for real application, such as medical image sharing between two remote hospitals.
The authors would like to thank the editor and anonymous reviewers for their constructive comments.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 |









