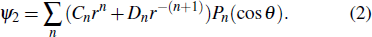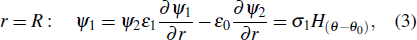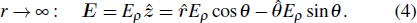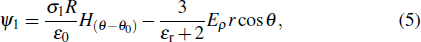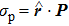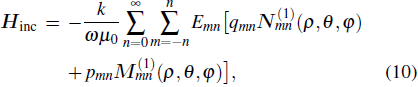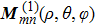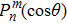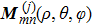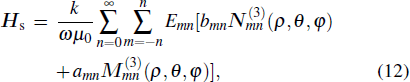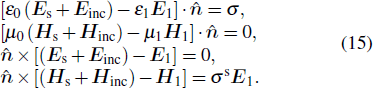Cite this Article
Li Xingcai, Gao Xuan, Wang Juan. Electromagnetic scattering of charged particles in a strong wind-blown sand electric field. Chinese Physics B, 2019, 28(3): 034208  
Permissions
Electromagnetic scattering of charged particles in a strong wind-blown sand electric field
Li Xingcai1, 2, †, Gao Xuan1, 2, Wang Juan3, ‡
School of Physics and Electronic-Electrical Engineering, Ningxia University, Yinchuan 750021, China
Ningxia Key Laboratory of Intelligent Sensing for the Desert Information, Ningxia University, Yinchuan 750021, China
Xinhua College, Ningxia University, Yinchuan 750021, China

 

† Corresponding author. E-mail: nxulixc2011@nxu.edu.cn jjxn1983@gmail.com

Project supported by the National Natural Science Foundation of China (Grant Nos. 11562017 and 11302111), the CAS “Light of West China” Program (Grant No. XAB2017AW03), adn the Major Innovation Projects for Building First-class Universities in China’s Western Region (Grant No. ZKZD2017006).

Abstract

Some field experimental results have shown that the moving sands or dust aerosols in nature are usually electrified, and those charged particles also produce a strong electric field in air, which is named as wind-blown sand electric field. Some scholars have pointed out that the net charge on the particle significantly enhances its electromagnetic (EM) extinction properties, but up to now, there is no conclusive research on the effect of the environmental electric field. Based on the extended Mie theory, the effect of the electric field in a sandstorm on the EM attenuation properties of the charged larger dust particle is studied. The numerical results indicate that the environmental electric field also has a great influence on the particle’s optical properties, and the stronger the electric field, the bigger the effect. In addition, the charged angle, the charge density, and the particle radius all have a specific impact on the charged particle’s optical properties.

PACS: 42.68.Ay;42.68.Ge;42.68.Mj
Keyword:wind-blown sand;electric field;extended Mie theory;charged particle;scattering
1. Introduction

Due to the negative impacts of aerosol on environment, climate, and ecosystem appearing,[1] some researchers begin to pay much more attention to the aerosol, especially in atmospheric science.[2] The sand/dust particle is an important composition of aerosols. In some related research processes, for example, the remote sensing of sandstorm and other aerosols, it is extremely important to accurately forecast the particle’s optical properties.[3,4] Therefore, some analytical solutions and the numerical simulation method have been proposed by many scholars.[3,5–8] However, in some cases, these methods can provide the accurately prediction results for the attenuation of electromagnetic (EM) wave in sandstorms,[9,10] in others, it maybe fails,[11] and there has been no any reasonable explanation until 2005. Some physical experiments of wind-blown sand have proved that the moving sands carry amounts of static charge, which also produce a strong electric field in the air,[12–14] the maximal intensity can reach up to 200 kV/m.[15,16] The theoretical researches, based on the Rayleigh approximation[17,18] or the Mie theory,[19–22] have shown that the charge on the particle surface can influence the optical properties of the particle,[23] and both the distribution angle and the surface density of the net charge have significant effects.[17–20,24,25] However, there have been no reports on the effect of the electric field so far.

Generally speaking, the dielectric particle immersed in an electric field will be polarized, its surface must have some polarization charge, and the magnitude is proportional to the strength of the electric field. If the electric field is strong enough, the order of magnitude of the polarization charge and the surplus charge will be the same. Therefore, they both can affect the particle’s optical properties. Nonetheless, there are no related reports published.

In view of this situation, this paper presents a theoretical model to discuss the effects of the environmental electric field on particle’s extinction properties. Firstly, the polarization charge is derived from the knowledge of electrostatics, and then the extinction efficiency of the charged particle immersed in a strong electric field is discussed. At the last, the effects of the distribution angle and the surface density of the net charge are analyzed.

2. The basically physical models
2.1. The polarization charge

As shown in Fig. 1, a partially charged spherical sand is immersed in an electric field of wind-blown sand. In this paper, we suppose that the particle radius is R and the permittivity is ε1. The surplus charge partially distributes on the particle, and the charge density is σ0, which uniformly distributes on a spherical cap of the sand, and the net charge distribution angle is 2θ0. The environmental medium is the air. The magnitude of the environmental electric field is Ep. Due to the electric polarization, the electric potentials inside and outside of the particle are ψ1 and ψ2, which can be expressed in the spherical coordinate as follows:[18]

Here Pn(cos θ) is the Legend function of the first kind, and An, Cn, and Dn are the unknown expansion coefficients, which can be determined by the boundary conditions
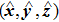
Here ε0 is the permittivity of the environmental medium, and H(θ − θ0) is the Heaviside function.[17] In this paper, we use a spherical polar coordinate system with coordinates (r, θ, φ) and a rectangular coordinate system with coordinates (x, y, z), the corresponding unit base vectors are and , respectively.

Fig. 1. Schematic drawing of partially charged sand in E-field illuminated by the EM wave.

Through Eqs. (1)–(4) and set εr = ε1/ε0, we can obtain the potential functions as follows:

The inner electric field of the charged particle is
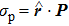
Then based on the equation P = ε0 (εr −1)Ein and , we can obtain the expression of the polarization charge[26]
Considering the net charge on the particle surface is σ0 which partially distributes on a cap of the sphere, the total charge on the particle is σ = σ0H(θ − (π − θ0)) + σp. In the next section, we will set it as a constant for every θ.

2.2. The extended Mie theory for partially charged sphere

Suppose that the incident wave is a z propagating plane wave characterized by the wave vector , where k = 2π/λ is the wave number, and λ is the wavelength. The electric field vector of the incident wave is Einc = E0 exp (ikz)x. The electromagnetic field of the incident wave can be expanded as follows:[27]

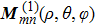
where ρ = kr, and are the vector spherical harmonics functions, and can be represented as follows:
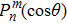
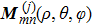
Here is the associated Legend function of the first kind, and for the function zn (ρ) in and , if j = 1, the function zn (ρ) is the spherical Bessel function of the first kind, named as jn (ρ), if j = 2, the function zn (ρ) is the spherical Bessel function of the second kind, named as yn(ρ), and if j = 3, the function zn (ρ) is the spherical Bessel function of the third kind, named as , with i being the imaginary unit. Then the interior field and the scattering field can also be written in the similar forms
The unknown coefficients can be determined by the boundary conditions[19,21]
Here σs is the surface conductivity, which can be obtained through the equation σs(σ) = i σq/[m(ω + irs)], and , σ is the surface charge density which can be derived from σ = σ0 H(θ − (π − θ0)) + σp present in the last section. m, q, and r are the mass, charge, and radius of the electron, respectively, N is the electron number, and T is the surface temperature.

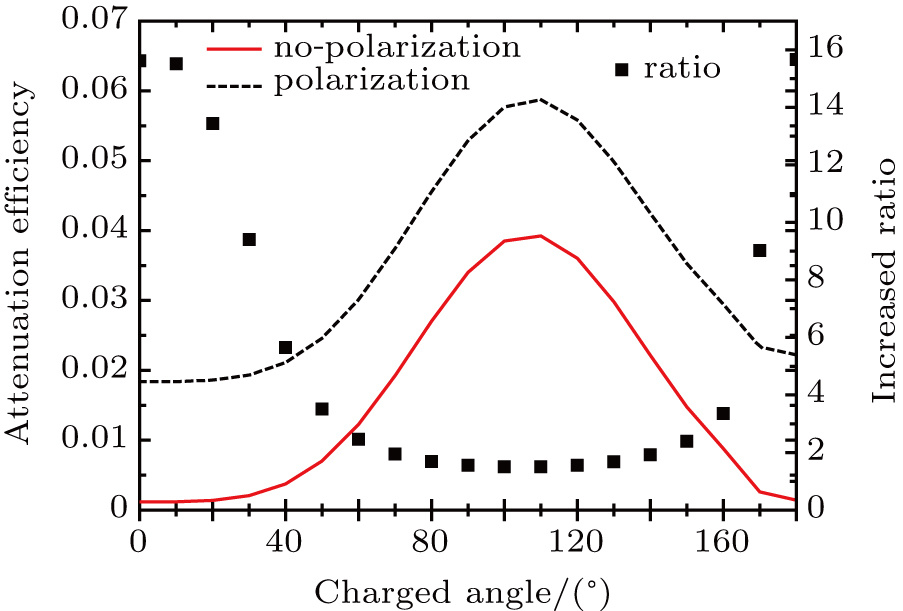
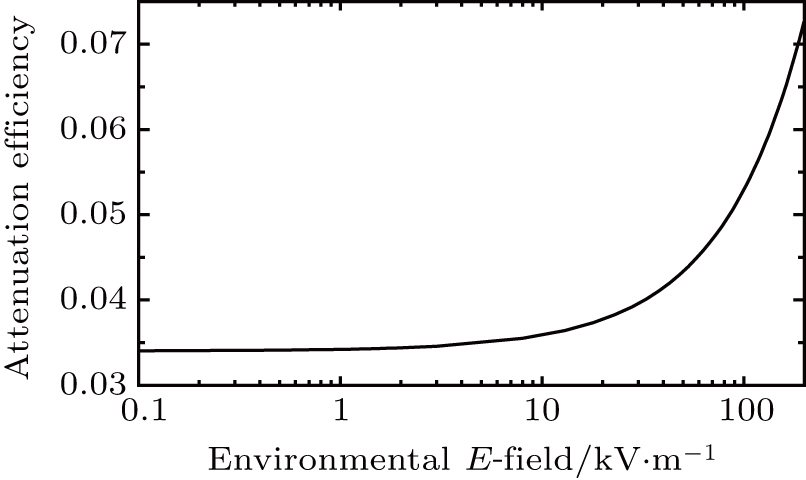
In principle, the electric polarization means that the positive charge in the material moves along the direction of the applied electric field, and the negative charge (usually, electrons) is reversed moving, thus one half of the particle surface is positively charged, the other half is negatively charged. For the nuclei, it is too large to produce a surface current with the action of the incident electromagnetic wave, but the electron can. So the valid charge which may contribute to the surface conductivity is just the negative ion (σp < 0). This means that the surface conductivity in Eq. (15) can be expressed as two parts, one is from the net charge, which can be calculated through σs(σ0H(θ − (π − θ0))), and the other one is from the polarization, which can be calculated from σs(σp H(θ − π/2). Here we have set σ0 as the net charge on the particle surface, σp as the polarization charge in Eq. (9), where H(x) is the Heaviside function.

Then through Eqs. (9)–(15) we can obtain

Through the above equations, we can obtain the expansion coefficients in Eqs. (9)–(14).

Then the particle’s extinction cross section can be obtained as

where subscripts i and s represent the incident field and the scattering field, and subscripts θ and φ represent the components of the field. The extinction cross section can be normalized by the particles' geometric cross section, and then we can obtain the efficiency factor
In the next section, we will use Eqs. (16)–(18) to discuss the electromagnetic scattering properties of the partially charged particle in a strong electric field.

3. Results and discussion

The parameters in the numerical calculation are as follows: the frequency of the incident wave is 9.4 GHz, the particle radius is 30 μm, the relative refractive index m = 1.5 + 0.1i, the relative permittivity εr = m2. The net charge density σ0 = −1 μ C/m2, and the intensity of the environmental electric field is Eh = 100 kV/m2. Without any special comments, the parameters remain unchanged.

Firstly, the effect of the electric field on the sand’s extinction efficiency is discussed, and the results are showed in Fig. 2. The horizontal coordinate is the logarithmic coordinate system, but the vertical coordinate is the rectangular coordinate system. From it we can know that when the intensity of the environmental electric field is larger than 3 kV/m, the effect of the electric field on the particle optical properties is significant, and with the electric field increasing, the effect becomes much stronger.

Fig. 2. The effect of environmental electric field on particle’s extinction efficiency.

In Fig. 3, the effect of the charge distribution angle on sand’s extinction efficiency is discussed, and we set the intensity of environmental electric field as 100 kV/m. The results show that, for a given charge density, the particle extinction efficiency firstly increases and then decreases with the charge distribution angle increasing, and when the charge distribution angle is 110°, it arrives at a maximal value. In addition, it is worth noting that the extinction efficiency of the charged sand in an electric field is much larger than the one without considering the effect of the environmental electric field.

Fig. 3. The effect of charge distribution angle on particle extinction efficiency in electric field.

The effect of the charge density is shown in Fig. 4. It can be seen that the particle extinction efficiency linearly increases with the increase of the surface charge density on the particle, and the values are much larger than those when the polarization charge is not unconsidered. Figure 5 reveals the effect of the particle radius on the optical properties. From it we can know that the particle extinction efficiency exponential changes with the increase of the particle’s radius, and the extinction efficiency when considering the polarization charge in strong electric field is much larger.

Fig. 4. The effect of charge density on particle’s extinction efficiency in electric field.
Fig. 5. The effect of particle radius on particle’s extinction efficiency in electric field.
4. Conclusion

Based on the extended Mie theory, the effect of the electric field in dust/sand storm on the sand’s optical properties is investigated. It is found that for the charged sand particle in sand storm with strong electric field, its optical properties are significantly influenced by the environmental electric field, and when the electric field exceeds 3 kV/m, the particle’s extinction efficiency enhances with the increase of the electric field intensity. The charged angle, charge density, and particle radius all have specific impact on the influence of electric field in charged sand’s optical properties. These results are important for the analysis of laboratory data and remote sensing information on sandstorm and rain-cloud parameters.

Reference
[1] Akhlaq M R Sheltami T Mouftah H T 2012 Rev. Environ Sci. Niotechnol. 11 305
[2] Mahowald N Ward D S Kloster S Flanner M G Heald C L Heavens N G Hess P G Lamarque J F Chuang P Y 2011 Annu. Rev. Environ. Resour. 36 45
[3] Mishchenko M I Travis L D Lacis A A 2002 Scattering, Absorption, and Emission of Light by Small Particles Cambridge Cambridge University Press 10.1002/978352761815
[4] Kokhanovsky A A 2013 Earth-Sci. Rev. 116 95
[5] Mishchenko M I Hovenier J W Travis L D 2000 Light Scattering by Nonspherical Particles, Theory, Measurement, and Applications San Diego Academic Press
[6] Ludwig A C 1991 Comput. Phys. Commun. 68 306
[7] Wriedt T 1998 Part. & Part. Syst. Charact. 15 67
[8] Wriedt T 2007 J. Quant. Spectrosc. Radiat. Transfer 106 535
[9] Elabdin Z Islam M R Khalifa O O Raouf H E A 2009 Prog. Electromagn. Res. 6 139
[10] Bashir S O McEwan N J 1986 IEE Proc. 133 241
[11] Dong Q Cong H 1996 Chin. J. Radio Sci. 11 29
[12] Zheng X J Huang N Zhou Y H 2003 J. Geophys. Res. Space Phys. 108 4322
[13] Zheng X J 2013 Eur. Phys. J. 36 138
[14] Zhai Y Cummer S A Farrell W M 2006 J. Geophys. Res. 111 E06016
[15] Bo T L Zheng X J 2013 Aeolian Res. 8 39
[16] Zhang H F Wang T Qu J J Yan M H 2004 Chin. J. Geophys. 47 53
[17] Zhou Y H He Q S Zheng X J 2005 Eur. Phys. J. 17 181
[18] Zhang B Li X 2014 J. Quant. Spectrosc. Radiat. Transfer 148 228
[19] Xie L Li X Zheng X 2010 Appl. Opt. 49 6756
[20] Li X Zhang B 2013 J. Quant. Spectrosc. Radiat. Transfer 119 150
[21] Klacka J Kocifaj M 2007 J. Quant. Spectrosc. Radiat. Transfer 106 170
[22] Klacka J Kocifaj M 2010 Prog. Electromagn. Res. 109 17
[23] Chen Y Y Xie A G Gu F Wang Q H Li Z H 2015 Indian J. Phys. 89 299
[24] Li X Xie L Zheng X 2012 J. Quant. Spectrosc. Radiat. Transfer 113 251
[25] Heinisch R L Bronold F X Fehske H 2012 Phys. Rev. Lett. 109 243903
[26] Xingcai L Dandan L Xing M 2014 J. Quant. Spectrosc. Radiat. Transfer 149 103
[27] Xu Y L 1998 Phys. Lett. 249 30