Ultrafast fiber lasers have a wide range of applications in various fields, such as optical frequency metrology, medicine, and precise materials processing.^[1–5] The passive mode-locking technique is one of the main approaches to generating ultrashort pulses. Several methods have been reported for realizing passive mode locking, such as nonlinear polarization rotation (NPR),^[6,7] nonlinear optical loop mirror (NOLM),^[8,9] and semiconductor saturable absorber mirror (SESAM).^[10,11] Compared with NPR and NOLM, the SESAM method offers better stability and self-starting performance.^[10] However, the drawbacks of SESAM, such as a low damage threshold and a small response bandwidth, have restricted the applications of SESAM in passively mode-locked fiber lasers, thereby promoting researches into new saturable absorbers (SA) such as carbon nanotubes and graphene.^[12–14]

Since 2009, when graphene, a new type of two-dimensional (2D) material, was successfully used for the first time as a new SA in ultrafast optics,^[15] it has attracted significant attention in the field of passive mode-locking technology owing to its fast recovery time, wide response bandwidth, and easy fabrication.^[16–18] In particular, compared to other SAs, such as carbon nanotubes and SESAM, graphene shows obvious advantages in the realization of ultrafast pulses because of the properties of broadband response.^[12] In addition to the above advantage, SAs based on graphene can be realized with various integration methods for fiber devices, which cannot be applied with SESAMs.^[19–23] Among these integration methods, the ones based on evanescent field interaction, such as graphene-tapered-fiber (GTF) SAs, are popular in the research of graphene mode-locking devices owing to their high damage threshold, long interaction length, and convenient manufacture.^[24,25]

Several researches on mode-locked fiber lasers using GTF SAs have been reported. These studies have various concerns, such as multiwavelength operation,^[26] tunable-bandwidth mode-locked fiber lasers,^[16] SAs with tunable modulation depth^[27] and high output power.^[28] However, among these works, there are few reports on wide-bandwidth mode-locked pulses. It is generally known that a large abnormal cavity dispersion limits the generation of pulses with wide spectra and narrow pulse durations. To obtain pulses with better performance, the net cavity dispersion must be further reduced to near zero.^[29,30] However, the decrease in the cavity dispersion causes poorer laser stability,^[31] thereby leading to higher requirements for the performance of SAs, such as a larger modulation depth and shorter recovery time.^[32] To date, the widest bandwidth of the output spectrum based on the GTF SA is 10 nm, realized with a net cavity dispersion of −0.094 ps².^[16] However, in the above report, no further investigation was conducted on the bandwidth of the output spectrum realized with smaller net cavity dispersion. Therefore, for the GTF SA, an interesting question is what is the best output performance that a GTF-SA-based mode-locked fiber laser can achieve with intracavity dispersion management? To answer this question, in this work, a GTF-SA-based erbium-doped passively mode-locked fiber laser with small net cavity dispersion was constructed. To calculate the net cavity dispersion accurately, the dispersion of the tapered fiber was taken into consideration, and it was calculated using finite-element analysis. With the compensation of the intracavity dispersion, the net cavity dispersion was reduced to −0.0317 ps². A wide-bandwidth mode-locking pulse was generated with a 3-dB bandwidth of 13.6 nm, which is the widest spectrum obtained with a GTF-SA-based erbium-doped mode-locked fiber laser.

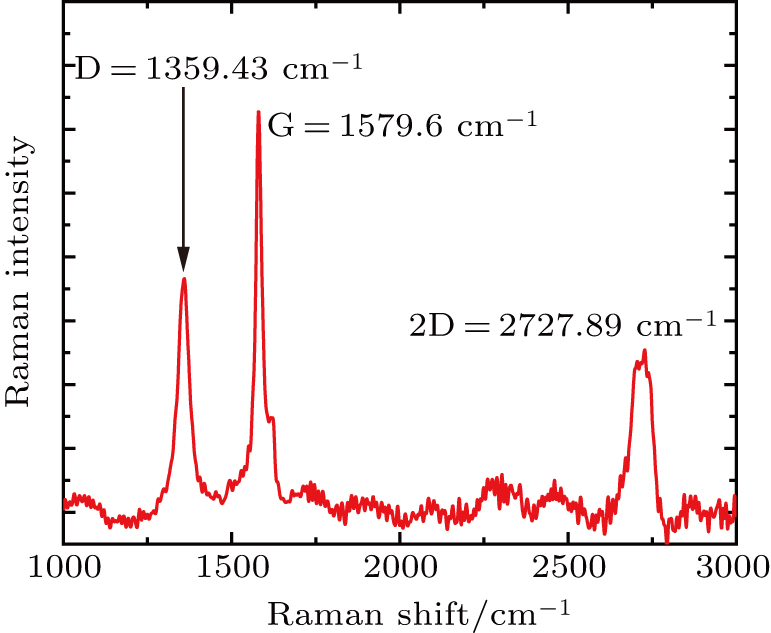
The modulation depth of graphene is proportional to its layer number. Multilayered graphene offers a larger modulation depth and is more suitable for ultrafast pulse generation than a single-layered one.^[12,33,34] A simple and effective method for obtaining multilayered graphene is liquid-phase exfoliation (LPE),^[35–37] which was applied in this experiment. During the preparation, 200 mg of graphite powder was mixed with 40-ml N-methyl pyrrolidone (NMP) and sonicated for 1 h. To deal with the material heating in the process of ultrasonication, the whole process was carried out in a circulating water bath with a temperature of 3 °C. Then, the mixture was centrifuged for 90 min with a rotary speed of 3000 rpm to separate graphene and large agglomeration. After the centrifugation, the upper liquid was collected as graphene dispersion.

Raman spectroscopy was employed to verify the effectiveness of the graphene preparation. The graphene dispersion was dropped on a slide glass substrate and dried at 50 °C as the test sample. The Raman spectrum of the sample was measured at an excitation wavelength of 488 nm. The result is shown in Fig. 1. The high intensity of the D peak indicates the defect of the exfoliated graphene, which is inevitably introduced during the sonication process.^[35] The wide band of the 2D peak implies that the exfoliated graphene is multilayered.^[38]

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Raman spectrum of the graphene prepared by LPE method in the experiment.

The tapered fiber was fabricated by an oxyhydrogen-flame stretching method with a segment of single-mode fiber (SMF-28). The waist diameter of the tapered fiber was approximately 3 μm. The intrinsic loss was measured as 0.01 dB at the wavelength of 1550 nm.

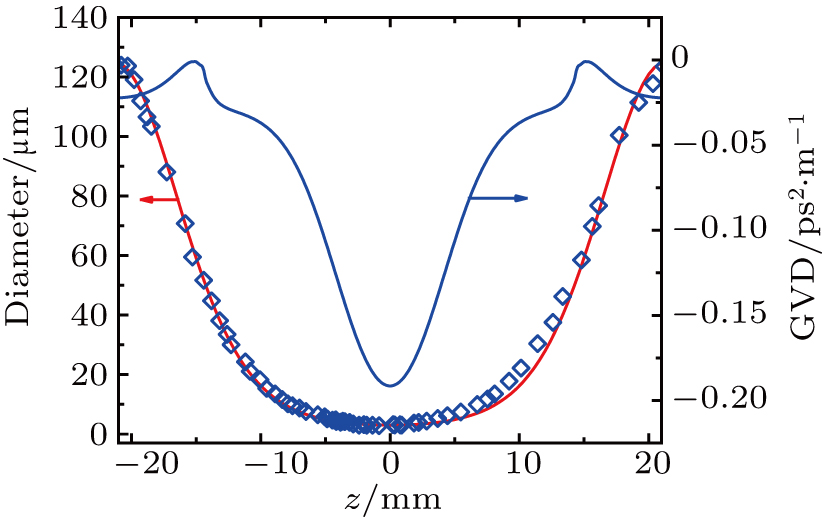
For better cavity dispersion management, the detailed group velocity dispersion (GVD) distribution of the tapered fiber was calculated. Initially, the shape of the tapered fiber was measured using an optical microscope. The shape of the tapered fiber can be expressed with the formula^[39]

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Shape of the tapered fiber (blue hollow squares: measured diameter; red solid line: numerical fitting) and the calculated dispersion distribution at 1550 nm along the z-axis of the tapered fiber (blue solid line).

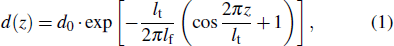To deposit the graphene onto the tapered fiber, the waist part of the tapered fiber was immersed in the graphene dispersion and an approximately 100-mW continuous wave laser at 1560 nm was injected into the tapered fiber. Because of the optical tweezer effect and light-induced swirl and convection, a graphene nanosheet was trapped and deposited onto the tapered fiber.^[40] After about 20 min, the deposition was completed. To guarantee a high enough modulation depth of the graphene SA, graphene nanosheets were deposited on the tapered fiber as much as possible, thereby leading to a large insertion loss. The insertion loss of the tapered fiber was measured as approximately 6.3 dB at 1560 nm. Using a microscope, it can be seen that the graphene nanosheets were deposited unevenly on the surface of the tapered fiber waist with a distribution length of about 150 μm.

The nonlinear optical absorption characteristic of the GTF SA was investigated using a balanced twin-detector system. The laser source used in the experiment was a commercial passively mode-locked erbium-doped fiber laser with a pulse width of ∼ 200 fs and a central wavelength of 1557 nm. The measured result is shown in Fig. 3, depicting the relationship between the input laser power and the transmittance of the graphene SA. Because of the limitation of the output power of the laser source, the GTF SA was not fully saturated in the measurement. Within the measurable range, the effective modulation depth was approximately 5%, and the unsaturated loss was around 69%.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Nonlinear absorption curve of the GTF SA.

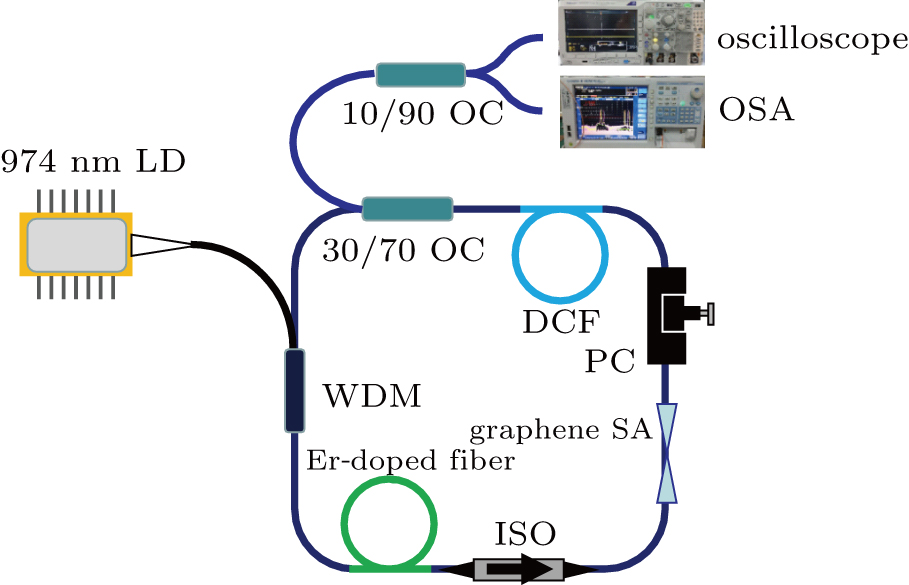
A passively mode-locked fiber laser was constructed, as shown in Fig. 4. The pump source was a Lumentum 360-mW laser diode (LD) with a peak wavelength of 974 nm. The LD was connected into the laser cavity through a 980/1550 wavelength division multiplexer (WDM). A segment of 0.85-m erbium-doped single-mode fiber (Nufern SM-ESF-7/125) was spliced with the 1550 arm of the WDM. After the erbium-doped fiber, a polarization-independent isolator (ISO) was applied to ensure unidirectional operation. A polarization controller (PC) was used for the control of cavity polarization. The output pulse was coupled out of the cavity through the 30% fiber of the 30/70 output coupler (OC). A dispersion compensation fiber (DCF) of approximately 1.6 m was employed to compensate for the abnormal dispersion of the laser cavity. The rest of the cavity was a single-mode fiber (SMF-28) with a length of 3.84 m. The GVDs of the SMF-28, erbium-doped fiber, and DCF were −0.023 ps²/m, −0.02 ps²/m, and 0.048 ps²/m, respectively, at 1550 nm. Considering the calculated dispersion of the tapered fiber, the net cavity dispersion was estimated to be −0.0317 ps². The 30% fiber of the 30/70 OC was connected to a 10/90 OC to divide the output signal into two ways. The output fiber was SMF-28 with a total length of around 2 m. The laser performance was simultaneously detected by a digital oscilloscope (Tektronic MDO 3102) and an optical spectrum analyzer (OSA Yokogawa AQ6370C).

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Experimental setup of the mode-locked fiber laser using the GTF SA.

When the pump power reached 67.5 mW, the laser output began to shift from continuous wave (CW) laser to Q-switched mode-locking pulses. When the pump power was increased to 79.8 mW, a CW-mode-locking pulse was obtained. The laser maintained the fundamental mode-locking working state until the pump power reached 116.4 mW. A further increment in pump power caused the mode-locked laser to work in the bound-soliton mode-locking regime. The relationship between the pump power and output power is shown in Fig. 5. The output power was measured at the 90% fiber of the 10/90 OC. The largest average output power of the fundamental mode-locking pulses was 0.442 mW, corresponding to a pulse energy of 13.5 pJ.

Fig. 5.

	Figure Option ViewDownloadNew Window
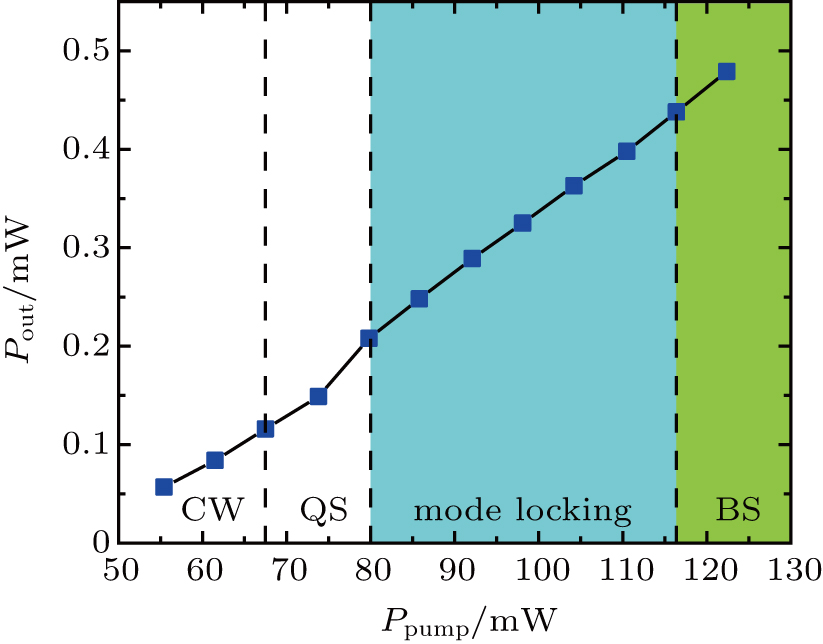	Fig. 5. Output power vs. pump power (CW: continuous wave regime, QS: Q-switched mode-locking regime, and BS: bound-soliton regime).

As shown in Fig. 6(a), the output spectrum with a 3-dB bandwidth of 13.6 nm was achieved at a pump power of 110.5 mW. The central wavelength of the spectrum was 1556 nm. In the spectrum, peaks were observed around the wavelength of 1530 nm, owing to the relatively large insertion loss of the GTF SA. The radio frequency (RF) spectrum was measured with a resolution bandwidth (RBW) of 10 Hz, as shown in Fig. 6(b). The repetition rate was 32.72 MHz, and the signal-to-noise ratio was 57 dB. Figure 6(c) shows the output pulse train with an interval of 30.6 ns corresponding to a cavity length of 6.33 m, thereby proving the single-pulse operation of the mode-locked fiber laser. As shown in Fig. 6(c), the pulse train has some intensity fluctuations, which may be caused by a fraction of output laser fed back to the laser cavity.^[41]

Fig. 6.

	Figure Option ViewDownloadNew Window
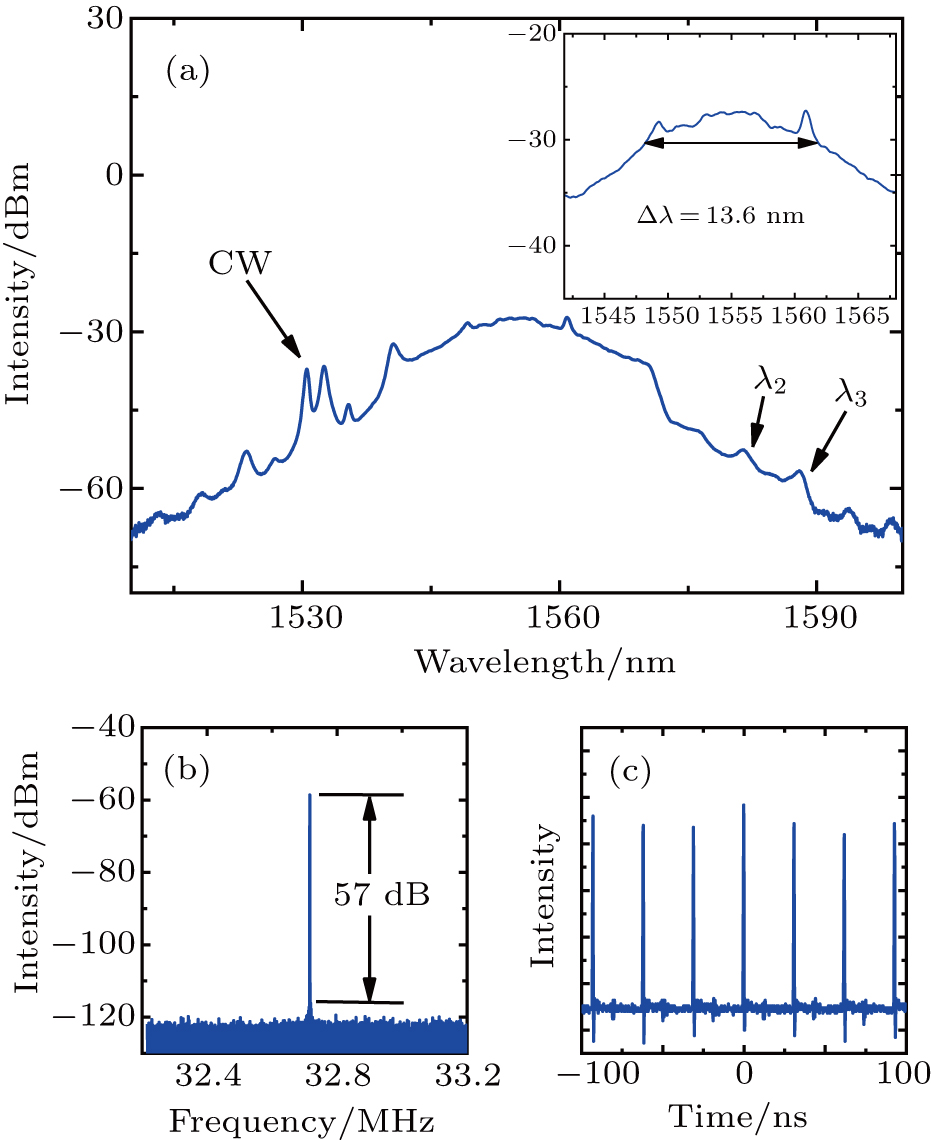	Fig. 6. Output pulse characteristics: (a) output spectrum with 3-dB bandwidth of 13.6 nm at a pump power of 110.5 mW, (b) RF spectrum, and (c) output pulse train.

Owing to the small output power and limitation of the experimental condition, the pulse duration could not be measured directly by the autocorrelator used in the experiment. To have a more complete understanding of the output performance, the pulse width was calculated based on the Kelly sideband position of the output spectrum. If the third- and higher-order dispersions are ignored, the position of Kelly sideband can be expressed as^[42]

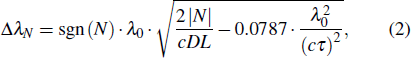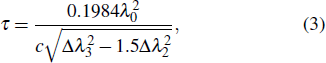The generation of the wide-bandwidth pulse can be attributed to the small net dispersion of the laser cavity. In the experiment, the length of DCF was set to be constant. The length of SMF-28 was changed to control the net cavity dispersion. As the SMF-28 became shorter, the net cavity dispersion gradually approached zero and the output spectrum became wider. When the length of SMF-28 was shortened to 3.84 m, the widest spectrum with 13.6-nm bandwidth was achieved. Further shortening the SMF-28 would narrow the spectrum bandwidth. The failure of the realization of stable mode-locked pulse with a 3-dB bandwidth wider than 13.6 nm may be because of the limitation of the modulation depth of the GTF SA.

The output performances of previous reports on erbium-doped mode-locked fiber lasers using GTF SAs are listed in Table 1. The output details of this work are presented at the bottom of the list. Among the results in Table 1, the laser presented here has outstanding performances both in spectral width and pulse duration, which can be attributed to the proper dispersion management of the laser cavity.

Table 1.

Table 1.

Table 1. Output performances of erbium-doped mode-locked fiber lasers incorporating GTF saturable absorbers. . Ref. Spectral Pulse Repletion Net cavity width/nm duration/ps rate/MHz dispersion/ps2 [20] 0.2 15.7 3.33 –1.02 [26] 0.24 11.8 8.034 – [16] 10 0.39 33.9 –0.094 [51] 2.08 1.12 1.89 –2.25 [52] 5.04 0.97 8.57 – [28] 0.85 7 1.67 –2.632 This work 13.6 ∼ 0.21 32.72 –0.0317

Table 1. Output performances of erbium-doped mode-locked fiber lasers incorporating GTF saturable absorbers. .

In this study, an erbium-doped passively mode-locked fiber laser based on GTF SA was demonstrated. With proper dispersion management, an output pulse with a 3-dB bandwidth of 13.6 nm was obtained, which is the widest spectrum ever achieved from a GTF SA-based mode-locked fiber laser. The output pulse had a repetition rate of 32.72 MHz and a signal-to-noise ratio of 57 dB.