† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11604164 and U1810129), the Fund for Shanxi “1331 Project” Key Innovation Research Team, China (Grant No. 1331KIRT), and Excellent Youth Academic Leader in Higher Education of Shanxi Province, China (2018).
Long range intermolecular interaction potential surface of CaF (2Σ+) was simulated by employing the MOLPRO program and using the RCCSD(T)/def2-TZVP theory. The predicted data were further fitted to obtain the collision cross-section. The elastic collision cross-section of CaF at the temperature around 2 mK is as high as 6.5×10−9 cm2 and the collision rate is over 4.1×106 Hz. Additionally, we found that an orientation electric field will simplify the intermolecular interaction potential function from quaternary into ternary and the collision cross-section will be raised by about three orders. All-optical evaporative cooling of cold CaF is discussed in the conclusion.
Cold molecular collision is one of the important aspects in the study of cold molecules. Quantum effects become important and even dominate the cold collision at low temperatures, where few partial waves contribute and the de Broglie wavelength associated with the relative velocity becomes comparable to or larger than the intermolecular distances.[1] Owing to the rapid progresses in the field of cold molecules in the past two decades, various cold molecules have been achieved experimentally, which has enabled investigations on cold molecular interaction and reaction.[2] Meanwhile, evaporative cooling appears to be the ultimate means to further cool the molecules to the μK region, and even to realize molecular Bose–Einstein condensation or Fermi-degeneracy, which is dominated by the molecular collision.
The calcium monofluoride (CaF) molecule has many potential applications.[3–6] The rovibronic ground state of CaF is high-field-seeking and no Majorana transition allows.[7] Additionally, when the temperature T fulfills kBT < 2hB, where kB is the Boltzmann constant, h is the Planck constant, and B is the molecular rotational constant, the inelastic collision is impossible,[8,9] which implies that there is little trapping loss. Thus, CaF is a good candidate for evaporative cooling. However, no molecule–molecule interaction of CaF has been reported so far.
At the RCCSD(T)/default-2 triple-zeta valence polarized (def2-TZVP) level, the interaction potential surface of CaF in the ground state X2Σ+ is fitted in the present work. Furthermore, the simplification of an orientation electrostatic field to the interaction potential is discussed. Our study shows that the collision cross-section will be enhanced significantly by the applied field. Finally, the evaporative cooling of CaF in an all-optical trap is also simulated.
Figure
CaF is an open shell molecule with electronic spin of 1/2, thus its dimer can either be a singlet (S = 0) or a triplet (S = 1). Therefore, the intermolecular interaction potential is determined by[10]
 |
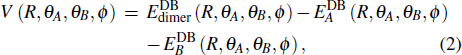 |
The four-dimension potential surface V(R,θA,θB,ϕ) in the molecular coordinates can be expanded in terms of spherical harmonics YL,M of degree L and order M as[10,17–19]
 |
 |
 |
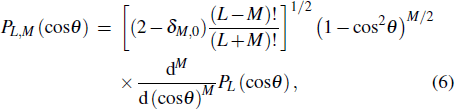 |
 |
Before computing the four-dimensional potential surface, we studied the CaF intermolecular interaction potential difference under the singlet and triplet systems. We computed the potential varying with the intermolecular distance with 27 sets of azimuthal angles. Some of these results are plotted in Fig.
We computed 32670 potential points employing MOLPRO program to obtain high precision potential surface VS=1(R,θA,θB,ϕ), and fitted to achieve 506 sets of vLA,LB,LAB(R). Some of the high order items, when Li = 10 and L > 10, appeared to be zero arose from the large separation azimuthal angles we set. If necessary, the high precision, high order items could also be determined. The obtained numerical potential points were non-linear least-squares fitted using Eq. (
 | Fig. 3. Partial of the non-linear least-squares fitted results of vLA,LB,LAB(R), where the dots were simulated and the lines were fitted. |
Different kinds of intermolecular interactions do not contribute equally to the collision cross-section. One has to determine the domination to estimate the cross-section. Liesbeth et al.[17] determined that the contribution of each coefficient to the interaction potential at the long range region can be expressed as
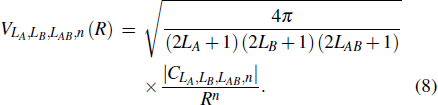 |
 | Fig. 4. The dipole–dipole (V1,1,2,3), dipole–quadrupole (V1,2,3,4), and dipole-induced-dipole (V0,0,0,6) interactions of CaF vs. intermolecular separation R. |
At the low molecular dense limit, the intermolecular elastic collision cross-section can be simplified as[20] (only considering the dipole–dipole interaction)
 |
 |
The investigation of intermolecular interaction is also in favor of cold molecular collision dynamics. The (ultra-)cold collision of CaF is very complex, and the quaternary potential surface function is hard either to analyze or understand, which are challenging to both the investigators and readers. Fortunately, CaF can be readily orientated due to both its relatively large permanent dipole and small rotational constant B = 0.3385 cm−1.[23] Figure
However, in a real case, the molecules cannot be fully orientated. We estimated that when the orientation degree is 0.96 obtained at the applied field of 100 kV/cm, only about 6% error of the cross-section arises. Therefore, in the high orientation case, the potential surface can be approximately determined using the simplified ternary model.
Additionally, the applied field to orientate the molecules will raise the intermolecular collision cross-section due to the field-induced molecular dipole, which depends on the polarizability. The polarizability tensor was calculated using the CCSD(T) theory on the basis of turbomole def2 series sets employing ORCA program,[27] and is listed in Table
| Table 1. Calculated component αzz of the polarizabilty tensor and molecular dipole μ at the CCSD(T) level in the basis of turbomole def2 series at different basis sets. . |
The induced dipole is 5.0×10−3 D at the applied field of 100 kV/cm. Figure
However, the dipole-induced-dipole interaction increases gradually with the decrease of the intermolecular distance—it would even overtake the dipole–dipole interaction, as shown in Fig.
 |
In addition, Ticknor[28] pointed out that the elastic collision cross-section of the ultracold molecules in high electric field is determined by the mass, induced electric dipole, and collision kinetic energy of the collision particles, and the cross-section does not depend on the detail of the short range interaction potential until it reaches the quantum unitarity limit σQ. The temperature corresponding to the σQ of CaF is 28 nK.[28] The elastic collision cross-section σSC of CaF at the temperature of 1 μK in the field of 100 kV/cm is as high as 1.2×10−8 cm2, larger than that of RbCs (3 × 10−9 cm2) under the same condition,[28] which further implies that CaF is a good candidate to be evaporatively cooled. Furthermore, the enhancement factor of the applied field to the elastic cross-section of CaF is over 2 × 103.
Other diatomic alkaline earth fluorides were also calculated and are listed in Table
| Table 2. Collision cross-sections of several diatomic radicals of alkaline earth fluorides. . |
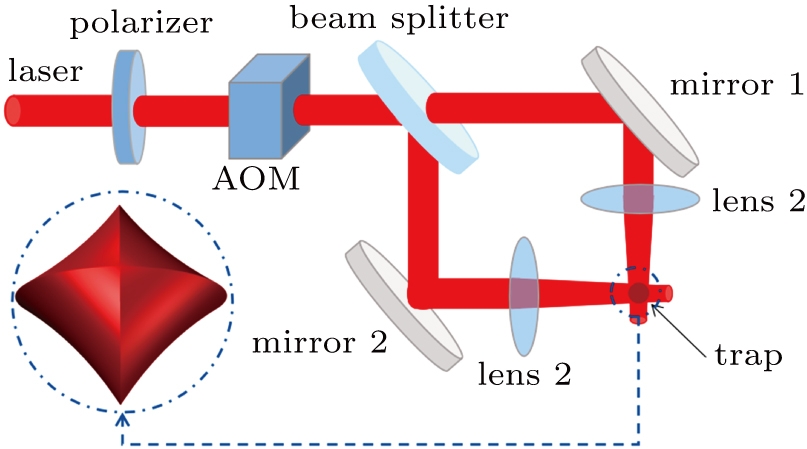
The setup for potential evaporative cooling of cold CaF molecules is illustrated in Fig.
 |
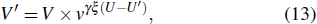 |
 |
 |
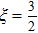
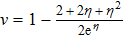
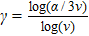
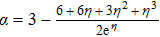
We simulated the CaF evaporative cooling in the proposed optical trap, as shown in Fig.
 | Fig. 9. (a) Molecular number N, (b) trapping volume V, (c) temperature T, and (d) molecular density n of CaF varying with time τ in the evaporative cooling procedure. |
The evaporative cooling of CaF presented above represents our preliminary discussion on a potential application of our cold CaF collision study. Detailed investigations, including short/long range intermolecular interaction in the singlet/triplet states, on the evaporative cooling is currently being undertaken by our group. The more precise molecular scattering cross-section will be determined by employing the MOLSCAT[31,32] program and the cooling process will be simulated and further optimized in the all-optical trap in our next work.
The long-range dipole–dipole interaction of CaF in its ground state was investigated in the present work by employing the MOLPRO program and using the RCCSD(T)/def2-TZVP theory. High precision molecular elastic collision cross-section and collision rate were obtained. At a temperature of 2 mK, the elastic cross-section of CaF molecules is as high as 6.5 ×10−9 cm2 and the collision rate is more than 4.1 × 106 Hz, which implies that CaF molecules are good candidates for evaporative cooling. Furthermore, the applied orientation electric field can simplify the molecular interaction potential surface function from quaternary into ternary, and can raise the collision cross-section by a factor of over 2000. Additionally, the evaporative cooling of CaF molecules (at 2 mK) in an all optical trap was discussed.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |