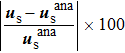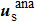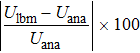† Corresponding author. E-mail:
We propose a boundary scheme for addressing multi-mechanism flow in a porous medium in slip and early transition flow regimes, which is frequently encountered in shale gas reservoirs. Micro-gaseous flow in organic-rich shale involves a complex flow mechanism. A self-developed boundary scheme that combines the non-equilibrium extrapolation scheme and the combined diffusive reflection and bounce-back scheme (half-way DBB) to embed the Langmuir slip boundary into the single-relaxation-time lattice Boltzmann method (SRT-LBM) enables us to describe this process, namely, the coupling effect of micro-gaseous flow and surface diffusion in organic-rich nanoscale pores. The present LBM model comes with the careful consideration of the local Knudsen number, local pressure gradient, viscosity correction model, and regularization procedure to account for the rarefied gas flows in irregular pores. Its validity and accuracy are verified by several benchmarking cases, and the calculated results by this boundary scheme accord well with our analytical solutions. This boundary scheme shows a higher accuracy than the existing studies. Additionally, a subiteration strategy is presented to tackle the coupled micro-gaseous flow and surface diffusion, which necessitates the iteration process matching of these two mechanisms. The multi-mechanism flow in the self-developed irregular pores is also numerically investigated and analyzed over a wide range of parameters. The results indicate that the present model can effectively capture the coupling effect of micro-gaseous flow and surface diffusion in a tree-like porous medium.
The accurate understanding of the fundamental flow mechanism of methane gas in complex micro/nanopores is crucial to the effective exploitation of unconventional reservoirs, the strata of which is associated with kerogen networks and organic matter. The unconventional reservoirs, such as shale reservoirs and other tight sandstone gas reservoirs, contain abundant micro-scale and nanoscale pores, the sizes of which vary in a wide range on a micro-scale from 2 nm up to 100 nm,[1] typically presenting multi-scale networks of pores. The non-Darcy flow, such as slip flow and early transition flow,[2] dominates in these multi-scale pore networks. In kerogen-rich pores, the coupled micro-scale effects and surface diffusion (induced by methane adsorption/desorption process) control the gas flows, involving a complex flow mechanism, while only the micro-gaseous flow exists in these inorganic pores in the absence of adsorption/desorption.
Despite its attracting significant research attention in recent years, the accurate flow mechanism of micro-gas in an organic-rich porous medium still has not been well addressed, because the existing models and parameters are geometry-dependent and not applicable to these irregular pores. Most of the current analytical models for micro-gaseous flow in organic/inorganic pores are limited to cases with simple geometries, such as tube and channel,[3–5] which are of limited applicability to shale reservoirs where complex irregular nanopores are ubiquitous. To our best knowledge, the multi-mechanism flow is still less understood, although some hypothetical models have been proposed to capture gas transport in organic nanopores considering surface diffusion.[3,4] Additionally, the experiment-based studies are less accurate due to the extremely low mass transport capability of shale and difficulty in controlling laboratory conditions.[6–9]
As a replacement or supplementary to experiments and theories, numerical simulation has become a promising and effective tool to research and reveal some micro-scale physical mechanisms which fall beyond the scope of experiments and theories. A variety of numerical models, such as molecular dynamics simulation (MD),[10–13] direct simulation of Monte Carlo (DSMC),[14,15] lattice Boltzmann method (LBM),[16,17] and traditional computational fluid dynamics (CFD), have been widely applied to the studies of micro-gaseous flow. Due to expensive computational costs, MD and DSMC have extremely restricted applications on a macroscale. The traditional continuum-based CFD models are of limited applicability to the rarefied gas flows where continuum assumption breaks down (e.g., Kn > 0.1). The LBM, originating from the kinetic theory of molecules,[18,19] is a mesoscopic numerical model. It achieves considerable success in modeling the near continuum regime flows ( Kn < 0.1), and has been tried in previous studies to treat rarefied gas flows in transition flow regimes within straight channels.[20–29] A series of LBM-based models with kinetic boundary schemes has been proposed to address micro-gaseous flow over curved surfaces in the slip and early transition flow regime.[30–38] Karlin et al.[35] first proposed a discrete form of the completely diffusive reflection, which can be applied to curved walls, but some studies revealed that this boundary overestimates the slip velocity at the wall for micro-Poiseuille flow. Following Karlin et al.’s work, a combination form of diffusive reflection and bounce-back scheme (namely the DBB scheme), proposed by Luo et al.[34] and Chai et al. almost at the same time,[32] has been used to model micro-gaseous flow in complex pores. In the DBB scheme, the 1st-order[34] or 2nd-order velocity-slip boundary condition[32] was incorporated into the LBM model by choosing an appropriate combination coefficient. The studies of Tao and Guo et al. expanded the applications of the DBB scheme to micro-flows over spheres in slip and early transition regimes.[33,37,38]
To date, despite the fruitful achievements in predicting the micro-gaseous flow in slip and early transition flow regimes via LBM-based models, little attention has been paid to the LBM-based modeling of the coupled multi-scale and multi-mechanism flow. The strategies appearing in previous literature can be summarized into five categories in terms of LBM-based modeling for the micro-gaseous flow considering surface diffusion. In the first category, the Langmuir slip model is incorporated into the LBM.[39–41] By using the non-equilibrium extrapolation scheme,[42] Fathi et al.[39] first developed an LBM-based boundary scheme to capture the multi-mechanism flow. Wang et al.[40] developed a similar boundary to account for the Langmuir slip model. In the boundary scheme of Wang et al., the strategies of Inamuro et al.[43] were used to handle the surface diffusion, and the slip velocity of free gas near to the wall was determined by a kinetic boundary scheme. However, extending their boundary scheme into inclined wall or curved wall was difficult for several reasons. Wang et al.[41] presented a new boundary scheme to take account of Langmuir slip boundary by utilizing the non-equilibrium extrapolation approach.[42] Again, only the cases with straight channels were validated and tested in their studies. In the second category, long-range forces are introduced into the LBM to consider gas adsorption/desorption and boundary slip (see Refs. [10], [39], [44], and [45] for details). In their studies, gas adsorption/desorption in organic pores was modeled by long-range forces between gas and wall, and the velocity-slip induced by micro-scale effect and rarefaction effect was simulated by kinetic boundary schemes. Nevertheless, the selection of some micro-parameters of long-range forces in these models, e.g., the interaction strength between gas and wall, wall’s density, is a challenging task. In the third category, some semi-analytical or analytical models are incorporated into the LBM.[46–49] Chen et al.[46] proposed a generalized LBM model to simulate the flow through a representative elementary volume (REV) scale porous medium considering the Klinkenberg’s effect, based on the permeability correction in drag force, then an REV-scale LBM model was developed to approach the multi-mechanism flow in the reconstructed shale matrix.[47,48] In the fourth category, the surface diffusion is considered as a moving boundary.[50–52] Ren et al.[50,53] developed the BSR or DBB boundary with a moving wall to study the coupling effect of micro-scale flow and surface diffusion, and the velocity of the moving wall equals the adsorbed-gas transport velocity. However, the constant pressure gradient was employed in their study to calculate the adsorbed-gas transport velocity, which did not reflect the real cases with complicated geometries. In the fifth category, the LBM and other numerical methods are coupled,[10,11] e.g., molecular dynamics.
As pointed out above, the LBM-based modeling for micro-gaseous flow considering surface diffusion in irregular organic-rich pores is still in its vacancy. In this study, a more accurate model is developed to address this issue and overcomes some existing defects. The rest of this paper is organized as follows. In Section
The lattice Boltzmann method is a mesoscopic numerical method for computational fluid dynamics. Using the multi-scale analysis developed by Chapman and Enskog, the Navier–Stokes equations can be recovered from the lattice Boltzmann equation. The expression of the lattice Boltzmann equation with external force can be given as follows:
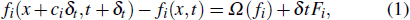 |
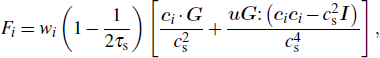 |
This study adopts D2Q9 model to predict the gas flow through a porous medium. Its velocity directions are defined as:
Usually, the collision operator Ω(fi) is a nonlinear integral differential expression in terms of particle distribution function fi(x,t). The well-known linearized collision operator Ω(fi) is employed and expressed as[16]
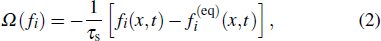 |
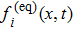
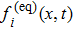
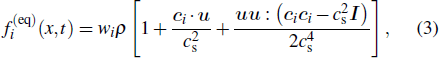 |
The macroscopic quantities, e.g., density ρ, velocity
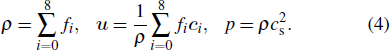 |
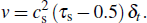 |
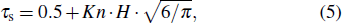 |
The adsorbed methane gas and free gas are coexistent in organic-rich pores. An accurate description of the coupling process of micro-gaseous flow and surface diffusion induced by adsorbed gas is under development and still has a puzzle. The universally adopted Langmuir slip model[39–41,54,55] is introduced to obtain the resultant slip velocity
 |
 |
We determine the diffusion velocity of adsorbed gas at wall with the strategies that combine the Maxwell–Stefan approach and Langmuir adsorption isotherm,[40] the effectiveness of which has been validated and confirmed by experimental and simulation studies. The diffusion velocity is expressed as[40]
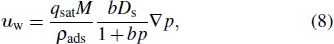 |
Note that three kinds of velocities are introduced into this study: the resultant slip velocity
The idea of non-equilibrium extrapolation scheme is that the unknown distribution functions of boundary nodes are approximated with the results of adjacent fluid nodes. At time step t, after collision and streaming step, the unknown distribution functions of a boundary node xb are decomposed into two parts as follows:[58]
 |
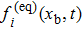
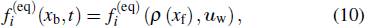 |
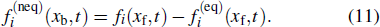 |
After obtaining the unknown distribution functions of boundary nodes at time step t, the unknown distribution functions of adjacent fluid nodes at time step t + 1 can be provided by the collision and streaming of their adjacent boundary nodes, which can be expressed as
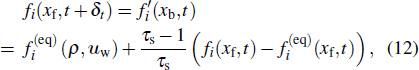 |
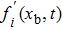
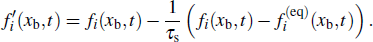 |
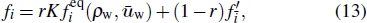 |

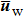
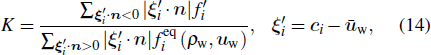 |
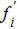
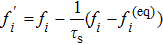
Considering Eq. (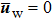
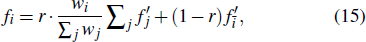 |
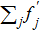
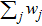
To include the 2nd-order slip boundary condition (e.g.,
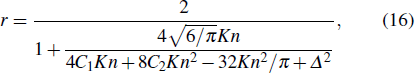 |
By combining Eqs. (
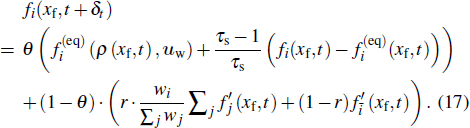 |
To ensure that the present SRT-LBM scheme is more accurate and stable in the hydrodynamic regime, a regularization step, developed by previous studies,[59–61] is embedded into this model to capture micro-gaseous flow at high Knudsen number. It filters out unnecessary higher-order contributions to non-equilibrium distribution functions to ensure that the non-equilibrium moments of the distribution functions satisfy the Hermite space.[60] The distribution functions are decomposed into the equilibrium and non-equilibrium parts as[60]
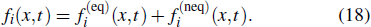 |
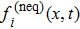
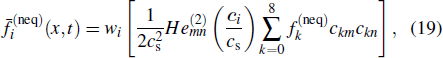 |
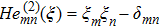
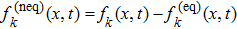
The evolution equation for the SRT-LBM model after being regularized is given as
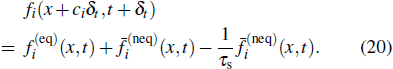 |
For the micro-gaseous flow in a porous medium, the Knudsen number is a local geometry-dependent parameter and associated with space location due to the spatial variation of its influencing factors, such as temperature, gas pressure, local characteristic length, etc.
For the hard sphere molecule, the mean free path λ of gas molecule can be expressed as[36]
 |
With Eq. (
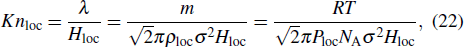 |
For pressure-driven micro-flows, the pressure gradient is also a space-dependent local parameter. To accurately capture surface diffusion and micro-scale flow along the surface, inspired by the research of Zhao et al.,[10,36] we propose a method to determine the local characteristic length and pressure gradient of free gas based on the following hypotheses: 1) the pressure variation of free gas along the transverse (or spanwise) direction can be neglected under an extremely low pressure difference at inlet and outlet; 2) the pressure gradient of free gas can be approximated by that of its nearest skeleton node of pore structures according to hypothesis 2); 3) the characteristic length of a fluid node equals that of its nearest skeleton node of pore structures, which can be reasonably accepted due to the definitions of the node’s characteristic length and skeleton of pore structures.
The detailed methods to approximately obtain the local characteristic length and pressure gradient of free gas are given below.
(I) The first step is to obtain the skeleton of pore structures. A thinning algorithm for digital patterns proposed by Zhang et al.[62] is employed in this study. It consists of two subiterations, aiming at deleting boundary points to obtain the skeleton of unitary thickness for random pore structures. A random porous medium and its skeleton line are shown in Fig.
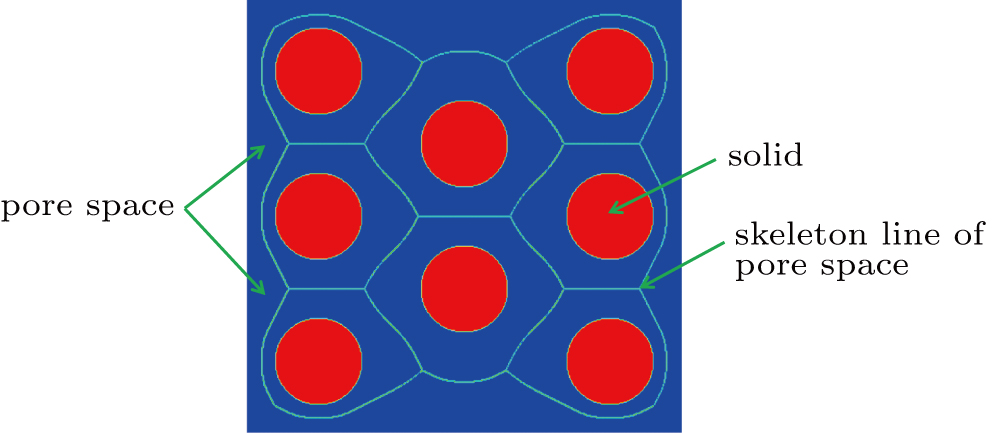 | Fig. 1. A channel filled with circular cylinders and calculated skeleton line by Zhang’s algorithm: the porous media and skeleton line of unitary thickness. |
(II) After obtaining the skeleton of pore structure, the local characteristic length of a skeleton point is determined by the maximal ball algorithm,[63] and then the local characteristic length of a fluid node is obtained under hypothesis 3).
(III) The pressure gradient of skeleton points is approximately obtained with difference approximation to partial derivatives, and then the pressure gradient of free gas is given by hypothesis 2).
With the local characteristic length of fluid nodes and local pressure gradient of free gas, we can easily implement the present boundary scheme in the LBM.
A few studies and numerical research[10,11,39–42,44,50–52] focused on the LBM-based modeling of multi-mechanism flow in micro/nanopores. However, most of them were only applied to a straight channel due to some limitations. The present scheme is built by coupling the non-equilibrium extrapolation scheme and halfway DBB boundary scheme, and later used to model multi-mechanism flow in a tree-like porous medium for its independence of the wall’s normal vector. The local Knudsen number for a fluid node and local pressure gradient along the skeleton line are also calculated to capture complex micro-flows along the irregular organic-rich pores. In addition, by considering viscosity correction and regularization procedure, the present model is capable of addressing high-Knudsen-number gas flows.
The micro-gaseous flow in a two-dimensional (2D) microchannel is employed to validate the proposed boundary scheme with Kn over a wide range. The gas flow is driven by a constant pressure gradient of ∂p/∂ x = 10–4, and the inlet and outlet are set as periodic boundary. The embedded Langmuir slip boundary (Eq. (

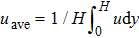
Gas flow driven by constant pressure gradient is the ideal case. However, the pressure-driven gas flow is more ubiquitous and significant in engineering applications. The micro-gaseous flow driven by pressure difference was modeled and validated in previous studies.[34,65] In this section, following the previous study,[65] we simulate the gas flow in a two-dimensional (2D) microchannel with height H and length L, and it is driven by a pressure difference between inlet pressure pin and outlet pressure pout. For isothermal micro-gaseous flow in the microchannel where the characteristic length of each fluid node is the height H, equation (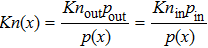
The size is set to be Nx = 2000 and Ny = 20 to ensure that the ratio of length over height is 100. The top and bottom walls are treated by the proposed boundary scheme, and the strategies of Verhaeghe et al.[34] are taken to address the pressure boundary at inlet and outlet. The outlet pressure pout is 1.0 / 3.0, and inlet pressure pin is set to be 1.4 / 3.0 for Kn = 0.0194 and 2.0 / 3.0 for Kn = 0.194. Figure
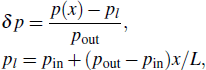 |
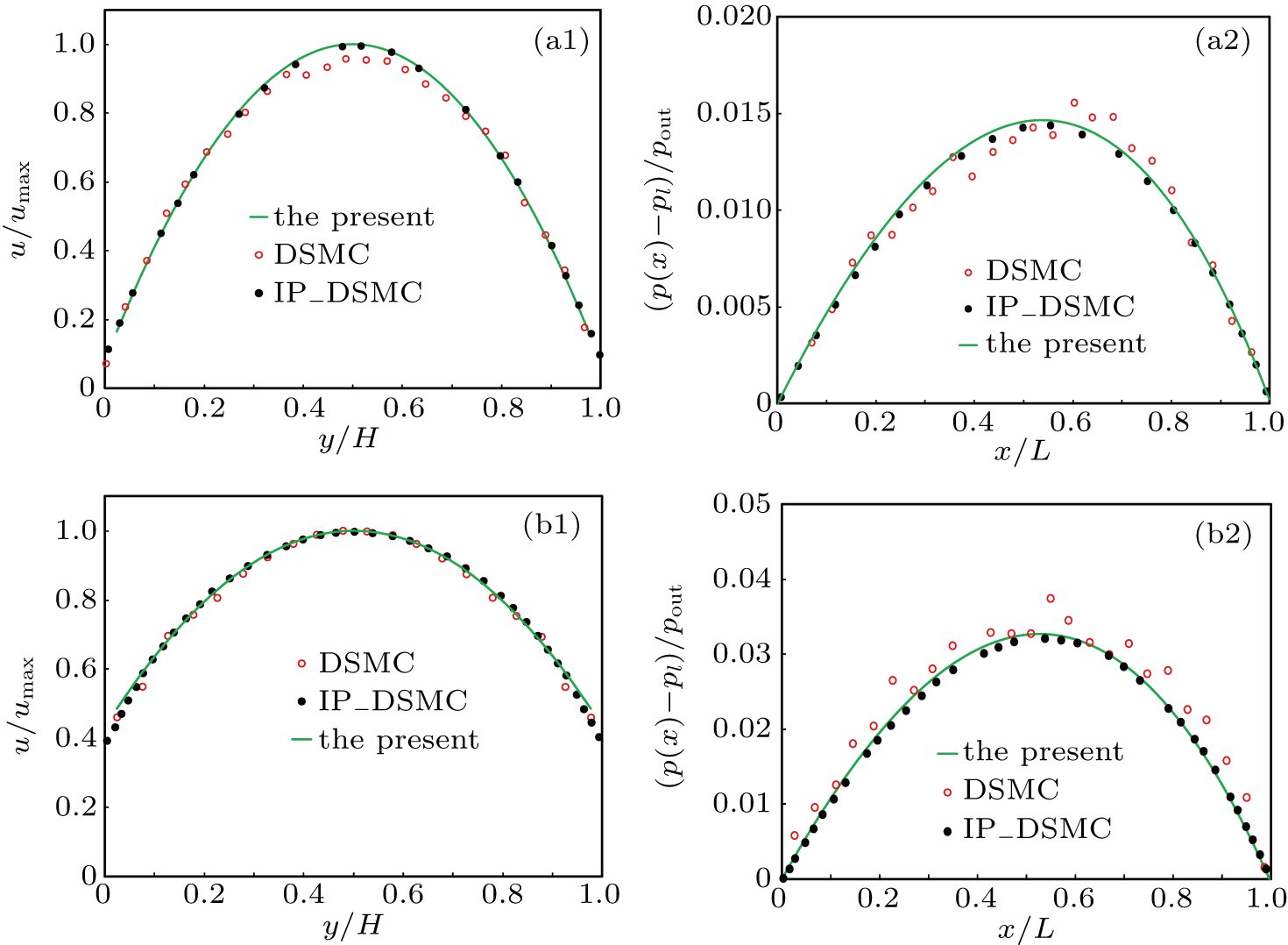 | Fig. 3. Normalized streamwise velocity profiles at outlet and non-dimensional pressure deviation along microchannel for (a) Kn = 0.0194 and (b) Kn = 0.194. Our numerical results are compared with results of Shan et al.[66] |
In Fig.
In the above two subsections, we verify that this boundary scheme is capable of modeling the micro-gaseous flow in slip and early transition flow regimes in a straight channel. In this subsubsection, we mainly check its accuracy and effectiveness in simulating the micro-scale gas flow considering surface diffusion. To include some existing results[40,41] for better comparison, we assume that
 |
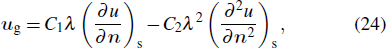 |
Then by combining Eqs. (
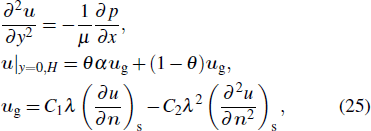 |
The analytical solution of Eq. (
 |
In this subsubsection, the present boundary scheme (Eq. (
We first choose the case with Kn = 0.0729 and θ = 1.0 to make comparisons with the existing results.[40,41] The size is set to be Nx = 2 and Ny = 500 for the periodic microchannel in use, and it is proven that this mesh size satisfies the mesh-independence. Figure
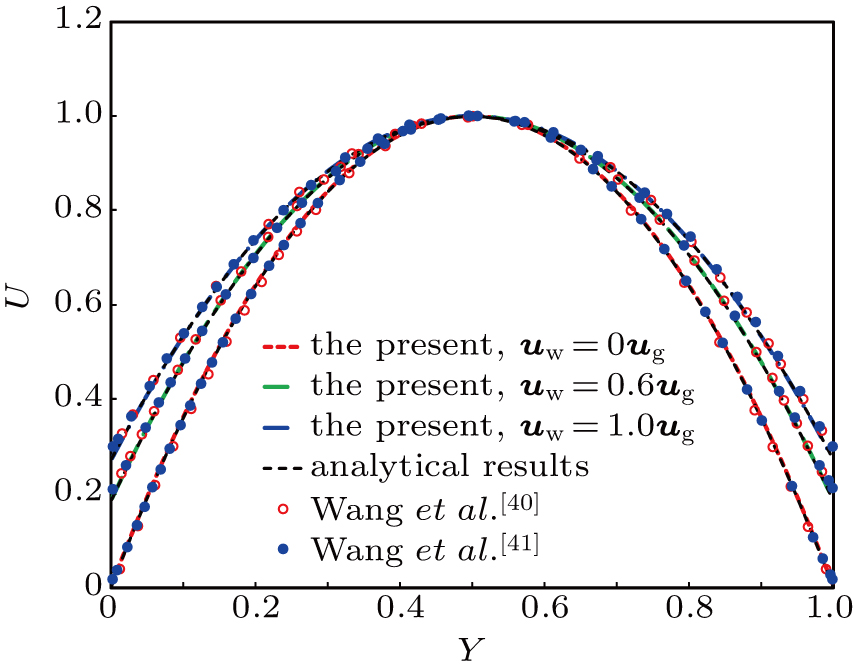 | Fig. 4. Comparison among the non-dimensional velocity profile predicted by the present model, analytical result, and previous studies (Wang et al.[40] and Wang et al.[41]) when Kn = 0.0729 and θ = 1.0. |
As is well known, the SRT-LBM model with bounce-back boundary will give rise to the viscosity-dependent unphysical issue when predicting velocity or permeability.[58,68–70] Actually, it is not induced by the SRT-LBM model, but by the bounce-back boundary and discretization errors.[18,69] The bounce-back boundary generally introduces an unphysical velocity-slip at static wall, which is associated with τs 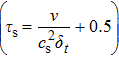
| Table 1. Normalized velocities at wall ( |
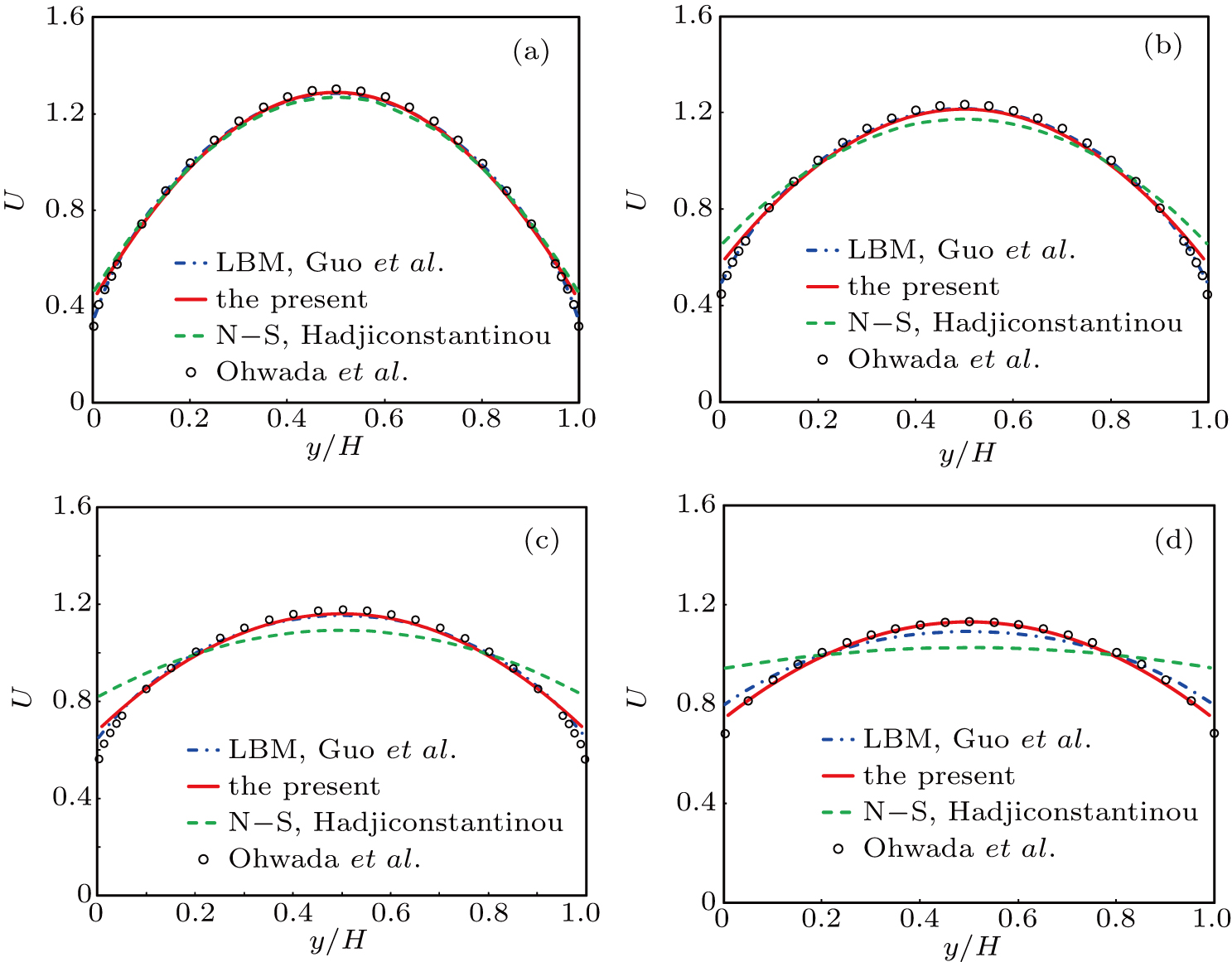
To further validate the proposed model, we carry out a series of validation cases with Kn (viscosities) and θ over a wide range. Our results are then compared with the analytical results from Eq. (
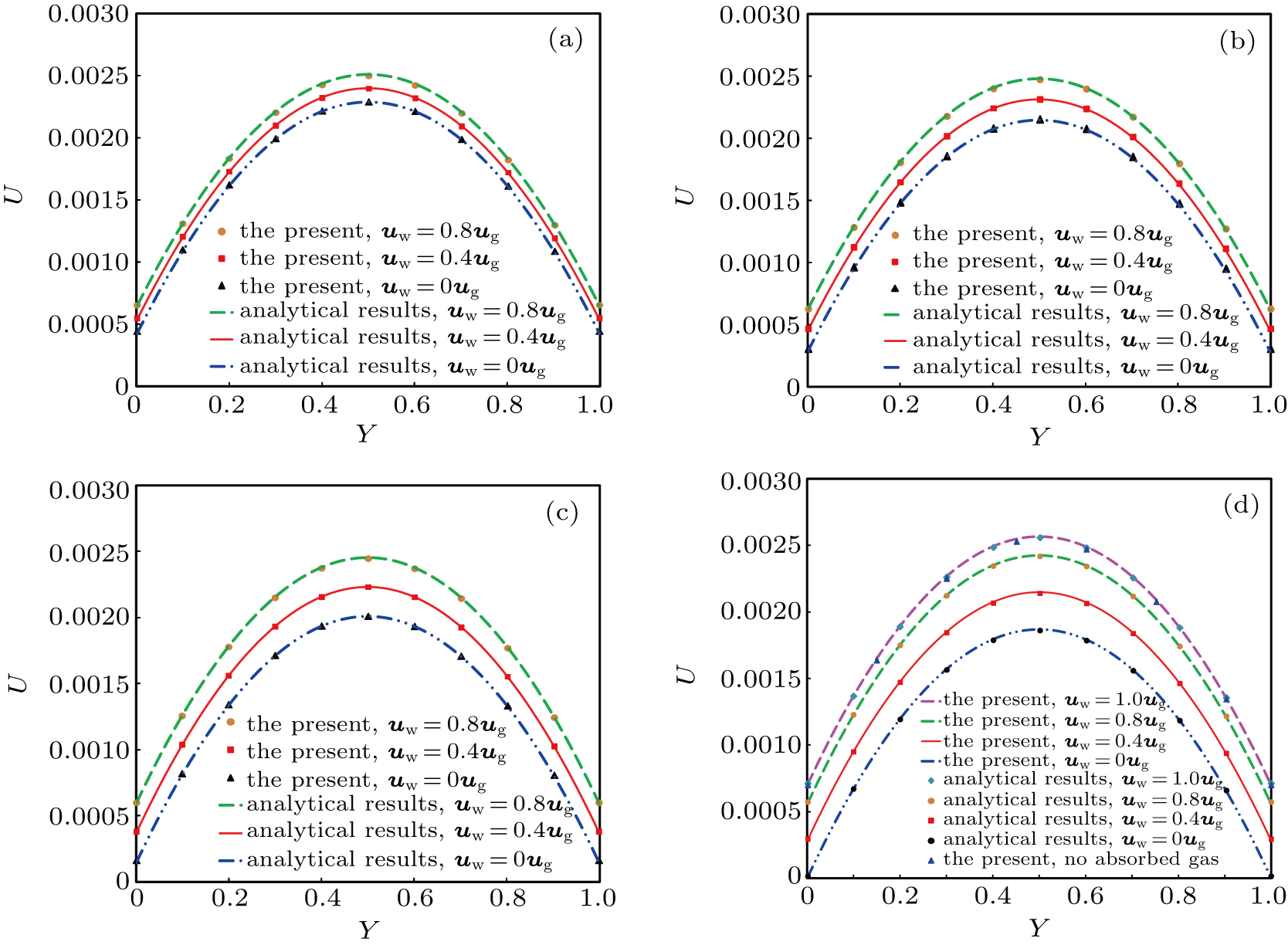 | Fig. 5. Comparison between streamwise velocity profiles predicted by the present model and analytical results (Eq. ( |
In the following parts, several cases with Kn = 0.01–0.12, within which the micro-gaseous flow in tight gas reservoirs mainly falls, are carefully investigated to further validate the present model. Again, all settings are consistent with the above validations in this subsubsection except for Kn. Our results show good agreement with analytical results when micro-gaseous flow considering surface diffusion falls within slip and early transition flow regimes as shown in Table
| Table 2. Relative errors of streamwise velocity between our numerical results and analytical results (Eq. ( |
In the following section, the micro-gaseous flow considering surface diffusion in self-developed tree-like porous medium is predicted by the present model.
The real pore structures of shale and sandstone can be reconstructed by experimental methods (e.g., computed tomography and focused ion beam scanning electron microscopy), numerical approaches (e.g., quartet structure generation set), and theoretical methods.[53] The popular theoretical models[53] are the bundle-of-tubes models, regular lattice model, circular model,[71] tree-like model,[72] etc. Inspired by the Sakhaee–Pour and Bryant’s works,[72] we adopt a tree-like model (see Fig.
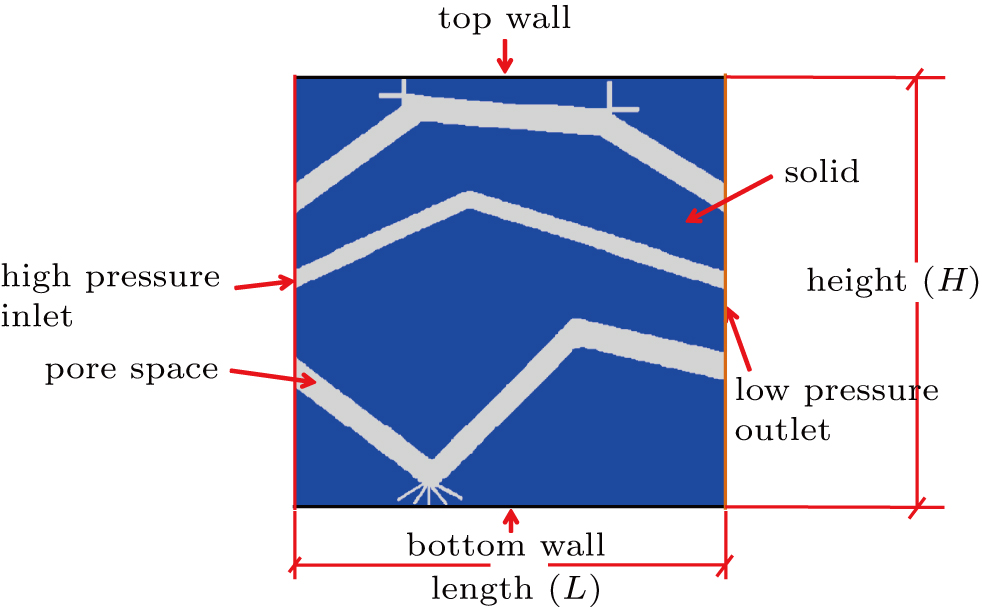 | Fig. 6. Boundary conditions and geometry of tree-like model: left and right boundaries are pressure boundaries, and the present scheme (Eq. ( |
| Table 3. Convention from physical units to lattice units (2D case). . |
In the above sections, all physical quantities (e.g., velocity, pressure) are non-dimensional parameters in lattice units, while all parameters have a specific physical unit in this section. Table
 |
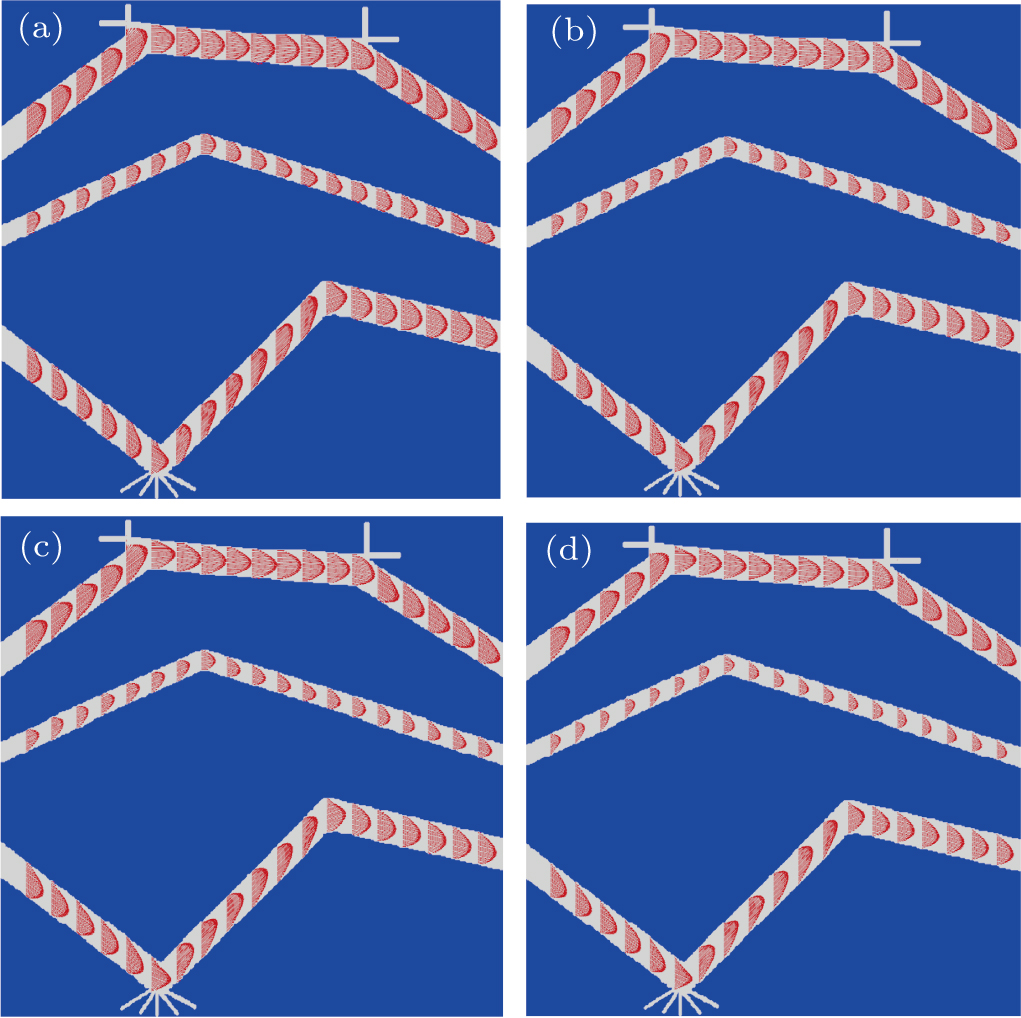
Figure
In Subsection
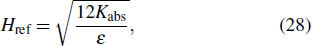 |
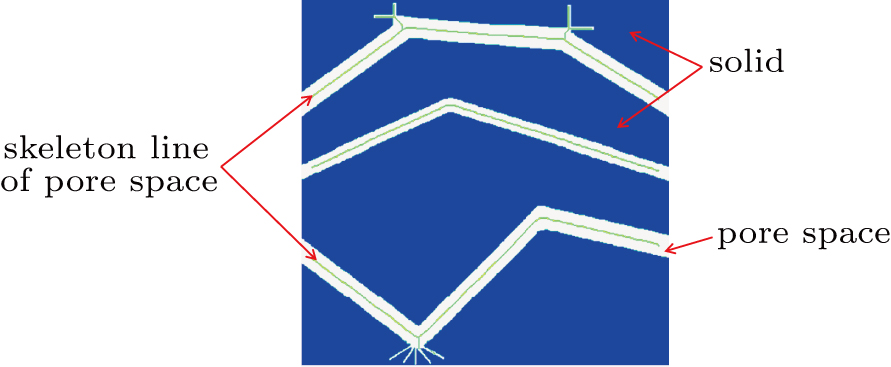 | Fig. 7. Skeleton line of tree-like model. Light green line represents skeleton line obtained via the method in Subsection |
The coupling process of micro-gaseous flow and surface diffusion involves two interconnected physical mechanisms. As shown in Eq. (
The first case begins with ∇ p = 0.1 MPa/m, pout = 10 MPa, Ds = 10–5 m2/s, qsat = 4000 mol/m3, b = 0.125 MPa–1, height = 75 nm and long = 75 nm. Figure
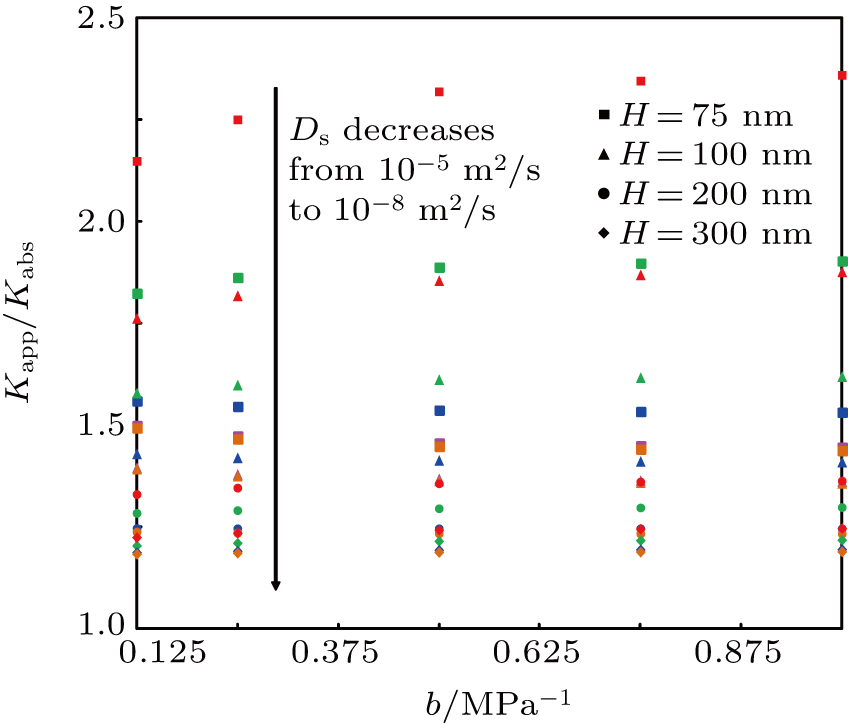
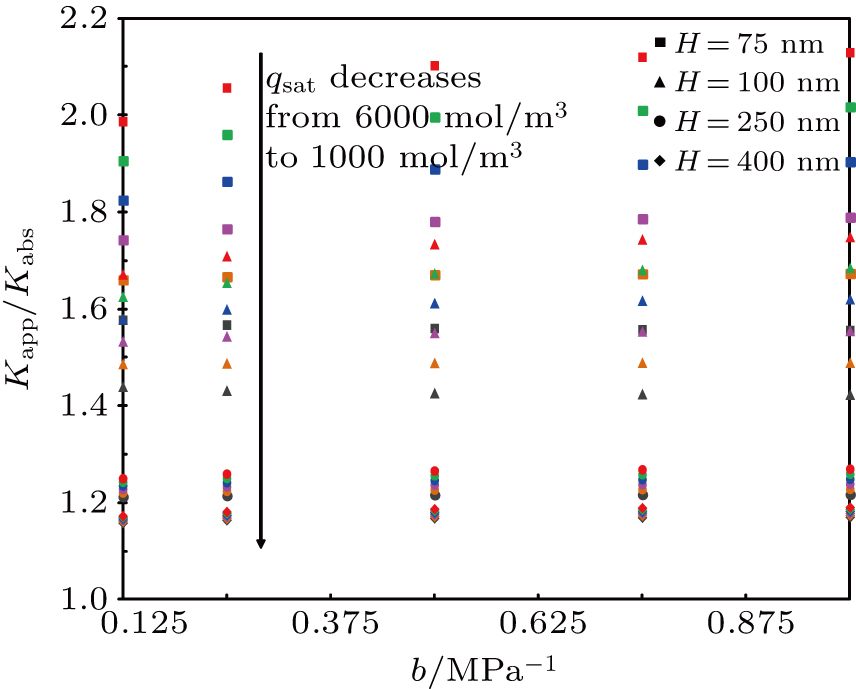
The apparent permeability Kapp as a function of pout, Ds, and H is shown in Fig.
Figure
In this section, the tree-like model composed of straight channels and inclined channels is employed to represent the shale matrix as done in previous studies.[53,72] Our validations above have carefully verified the present scheme, and it can be directly extended to addressing the tree-like model, which was evinced by previous studies.[18,32,42] Moreover, to some extent, our results are in agreement with Wang et al.’s results.[40] Therefore, the present model can effectively simulate multi-mechanism flow in the tree-like model.
Methane gas flow in organic-rich pores involves the coupling effect of multi-scale and multi-mechanism flow, specifically, the coupling of micro-gaseous flow and surface diffusion caused by methane adsorption/desorption in the pores. In this study, an LBM-based boundary scheme, which combines the non-equilibrium extrapolation scheme and half-way DBB scheme, is proposed to address this coupling effect by incorporating the Langmuir slip boundary into the single-relaxation-time lattice Boltzmann method. Several conclusions can be drawn as follows.
1) An algorithm for thinning digital patterns is employed to obtain the skeleton of pore structures, through which the local Knudsen number for a fluid node and local pressure gradient along skeleton line are calculated for better capturing micro-gaseous flow and surface diffusion along irregular organic-rich pores. By considering viscosity correction and regularization procedure, the present model can effectively resolve the high Knudsen number gas flows. Additionally, a subiteration strategy is proposed to address the coupling effect of micro-gaseous flow and surface diffusion.
2) The present scheme can effectively capture the coupling effect of micro-gaseous flow and surface diffusion in organic pores. An analytical solution under some assumptions is derived to further validate the present model, and good agreement is observed between our numerical results and analytical solutions. In addition, it achieves a higher accuracy than the existing studies, and also has the potential in modeling multi-scale and multi-mechanism flow in irregular pores. This study has extended it to simulate the multi-mechanism flow in a tree-like porous medium. Its effectiveness and accuracy are verified by the benchmarking cases and the comparisons with the existing results.
3) Multi-mechanism flow in the tree-like model is also numerically investigated and analyzed in a wide range of parameters. Our predicted results are consistent with Wang et al.’s results,[40] indicating that the present model is capable of modeling the multi-mechanism flow in irregular micro/nanoscale pores.
Our future work aims at extending the application of the present scheme to the complicated porous media and three-dimensional (3D) cases with GPU (CUDA C) platform.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] |