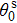Warm dense matter, which demonstrates complicated physics due to strong interactions between particles,^[1] is encountered in many engineering applications and fundamental research, such as cosmogony, inertial confined fusion, and Z-pinch. As an intermediate state between cold condensed matter and hot plasmas, warm dense matter is characterized by high densities as typical for condensed matter and temperatures of several eV.^[2] The equations of state (EOS) in solid and ideal plasma states have already been established using perturbation theory and statistical physics, respectively. However, those theories are not feasible to calculate the properties of warm dense matter, in which partial ionization, strong correlations, and quantum effects are important, resulting in immense challenges to describe the behavior of warm dense matter accurately.^[3]

EOS determines the fundamental thermodynamic properties of matter in hydrodynamic simulation. It is a crucial tool in interpreting the experimental results of warm dense matter.^[4] The impressive progress in pulsed-power technology and diagnostics of high spatiotemporal resolution gives a great motivation in the investigation of warm dense matter.^[5] The advanced experimental methods, such as dynamic compression using pulsed-power generator,^[6] ablation with high-intensity laser,^[7] generate extensive data of pressure to verify the EOS model. Since the warm dense matter occupies a broad range of phase diagram, a certain theory employed in EOS computations in specific density–temperature plane is difficult to cover the whole warm dense matter region. For instance, the chemical equilibrium model, in which several significant non-ideal effects are taken into consideration based on partially ionized plasma model, is commonly adopted to describe the thermodynamic properties for hot dense vapor and plasma.^[8] Generally, different theories should be applied to the corresponding application range with special treatments in the transitional region to produce a global EOS table, such as the most commonly used SESAME database.^[9] Much endeavor has been devoted to improve the prediction of EOS model in warm dense matter regime. Although the molecular dynamics and quantum Monte Carlo approaches have been employed in EOS computations,^[10] applying reasonable models in different states to construct semi-empirical EOS model with corrections of experimental data is still a popular method. Bushman et al. developed a generalized semi-empirical EOS model for metals over a wide range of pressure and temperature.^[11] Because it is easy to apply to different kinds of metallic materials with considerable accuracy, the multi-phase EOS model is further developed by Lomonosov.^[12] The semi-empirical EOS model contains a number of adjusting parameters, which are fitted by relevant experimental data. The Frankfurt equation of state, which is applied to study the dynamics of volumetrically heated matter passing through the liquid–vapor metastable states, is developed based on the quotidian equation of state (QEOS) scheme and, in principle, capable of generating EOS data for arbitrary materials as a function of density and temperature.^[13] Although much work has been devoted to the EOS computations, the construction of EOS model of relatively high accuracy in warm dense matter regime remains a challenge.

In this paper, a semi-empirical EOS model for aluminum in warm dense matter regime is established. The EOS model consists of cold term, thermal contribution of ions, and thermal contribution of electrons. The key parameters in cold term and thermal contribution of ions are determined based on relevant experimental data. The thermal contribution of electrons is calculated by Thomas–Fermi–Kirzhnits model with some practical modifications. The theoretical results derived from the semi-empirical EOS model are compared with relevant experimental data and other theoretical calculations.

The EOS model is subdivided into a cold term, thermal contributions of ions and electrons. The cold term is merely a function of density. The pressure P and internal energy E at a given density ρ and temperature T are expressed as follows:

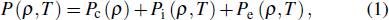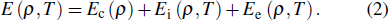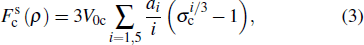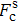
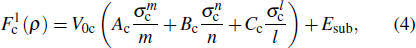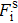
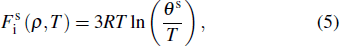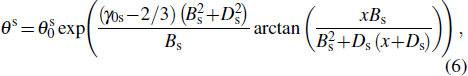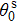
The thermal contribution of ions in solid state, , is calculated by high temperature approximations of Debye theory as^[11]

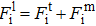
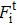
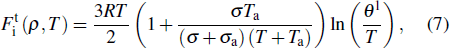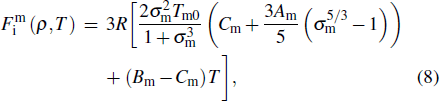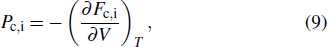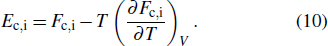The thermal contribution of ions in liquid state . Here is the anharmonicity of ions at high temperatures^[12] and ensures that the free energy is close to the asymptote of ideal gas in the high-temperature region

In the present work, the model for the thermal contribution of electrons is identical in solid, liquid, gas, and plasma states. The Thomas–Fermi–Kirzhnits model is applied to calculate the thermal contribution of electrons. The Thomas–Fermi model, which was initially developed to study the electron distribution of multi-electron atom, exhibits good performance for high Z (atomic number) elements. Since its advent, this model has been widely used in the EOS computations with advantages of clear physical picture and wide range of application.^[15] The Thomas–Fermi model describes the behavior of electrons within an atom of Wigner–Seitz radius with the distribution of electron density ρ(r) expressed as

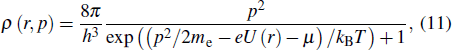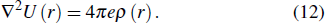The second-order differential equation for the Thomas–Fermi model can be derived from the above equations with the parameter transformation of dimensionless potential φ(x) = x(μ + eU(r))/k_BT and Fermi integral F_j. The Thomas–Fermi equation is expressed as

The Thomas–Fermi model, which yields a pressure of a few GPa under normal density at low temperatures, is only valid in the region of high compression ratio. In order to enlarge the application region of the Thomas–Fermi model, several corrections have been proposed to reduce the pressure to a reasonable level. Dirac introduced the electron exchange correction into the Thomas–Fermi model.^[17] Later, the quantum effect, which had been proven to be an additional predominating term, was taken into consideration.^[18] The Thomas–Fermi model with quantum and exchange corrections is denoted as the Thomas–Fermi–Kirzhnits model.^[19] The perturbation equations of exchange and quantum corrections for the Thomas–Fermi model are respectively

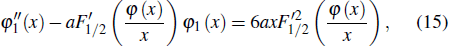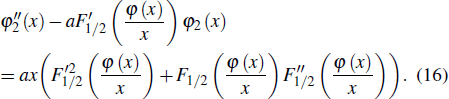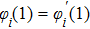
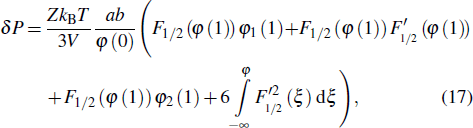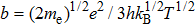
The cold contributions of ions and electrons are included in the cold term of the EOS model. Therefore, the thermal contribution of electrons is estimated by the Thomas–Fermi–Kirzhnits model with subtraction of the zero-temperature part. The pressure generated by the Thomas–Fermi model is substantially reduced with the quantum and exchange corrections taken into consideration. It is found in the construction procedure of the present EOS model that the correction value for electrons is much larger than that predicted by the Thomas–Fermi model in a certain region, resulting in a large negative pressure for the thermal contribution of electrons. The negative pressure for electrons acts as a binding force in a material, however, this effect has already been included in the cold term. This factor may be responsible for the obvious deviation between the theoretical calculation based on the Thomas–Fermi–Kirzhnits model and experimental measurements. The Thomas–Fermi–Kirzhnits model is applicable in the region where the exchange and quantum corrections are no larger than the thermodynamic parameter of the Thomas–Fermi model.^[21] This definition is adopted in the present EOS model. The thermal pressure of electrons P_e is calculated by the following practical modification in the present work:

Fig. 1.

	Figure Option ViewDownloadNew Window
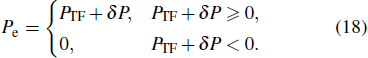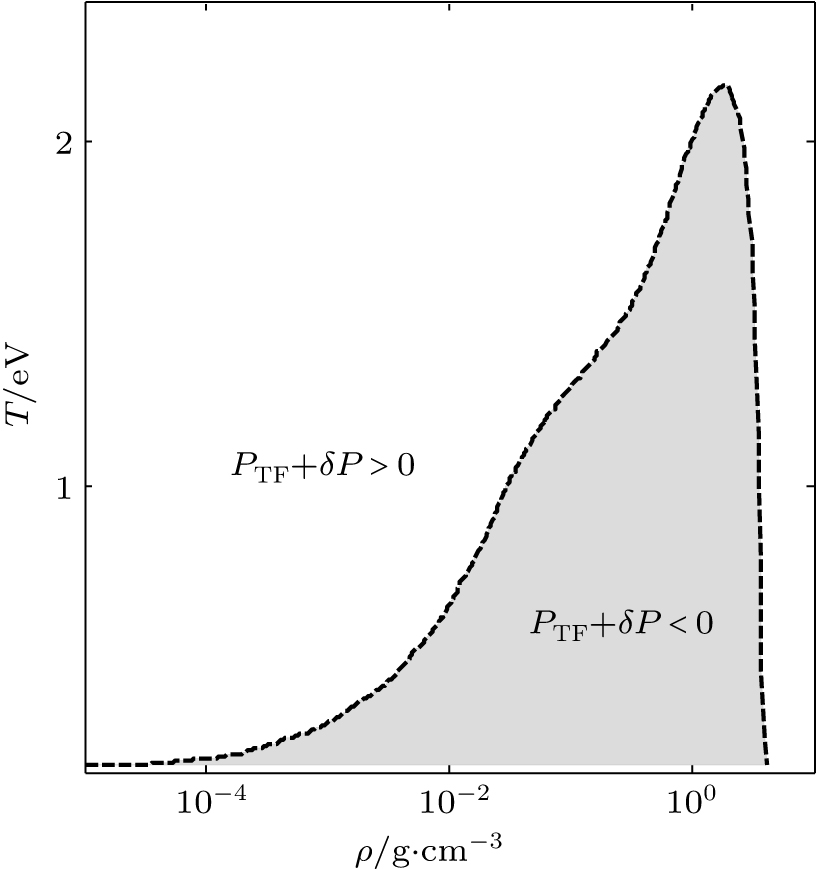	Fig. 1. The temperature–density boundary of PTF + δP = 0 for aluminum calculated from the Thomas–Fermi–Kirzhnits model.

The operator expansion of the electron distribution used to evaluate the corrections in the Thomas–Fermi–Kirzhnits model appears to be asymptotic near the normal density at low temperature, yielding overcorrection to the pressure and internal energy.^[19] This deficiency produces negative internal energy for the thermal contribution of electrons at low temperatures. The negative internal energy is encountered in some EOS models in certain density–temperature domain.^[13,22] Generally, a normalization treatment is designed to generate non-negative minimum internal energy and pressure under normal conditions.^[23] In the present work, the exchange and quantum corrections are not included in the electronic internal energy term to avoid negative total internal energy, making the EOS model approximately correct in this region.

Semi-empirical model is an important approach to calculate global EOS table for simulation of high energy density physics phenomena. The semi-empirical EOS model generates EOS data of different metal materials with relatively high accuracy and less calculation by adjusting several undetermined parameters. The fitting parameters in Table 1 for aluminum are determined based on the method described in the above section. In the construction process of the EOS model, the temperature, density, pressure, and internal energy are in units of kK, g/cm³, GPa, and kJ/g, respectively.

Table 1.

Table 1.

Table 1. Fitting parameters in the EOS model. . Variable Value Variable Value Variable Value V0c 0.3614 Bc 40.96 Ds 0.36 a1 326.35 Cc −28.05 σa 0.923 a2 −1035.4 m 8.0 Ta 30.0 a3 851.51 n 4.99 σm0 0.923 a4 −160.59 l 0.7 Tm0 0.933 a5 11.17 0.1 Am 2.24 Esub 12.098 γ0s 2.19 Bm −5.64 Ac −12.91 Bs 0.6 Cm 0.21

Table 1. Fitting parameters in the EOS model. .

Abundant pressure data at ambient temperature have been accumulated from a large number of isothermal compression experiments. Those data provide good benchmark for the cold term of EOS model in compressed solid state, because the thermal contribution constitutes a very small proportion of the results in compressed solid state at ambient temperature. The isothermal compression curve at ambient temperature calculated by this EOS model is presented in Fig. 2. The relevant experimental data^[24–26] and theoretical evaluation^[27] are also plotted for reference. The cold pressure is slightly lower than the pressure at room temperature. Generally, one can see from Fig. 2 that the isothermal compression curve agrees well with the experimental data, indicating that this EOS model generates reasonable predictions in the high-density region at low temperatures.

Fig. 2.

	Figure Option ViewDownloadNew Window
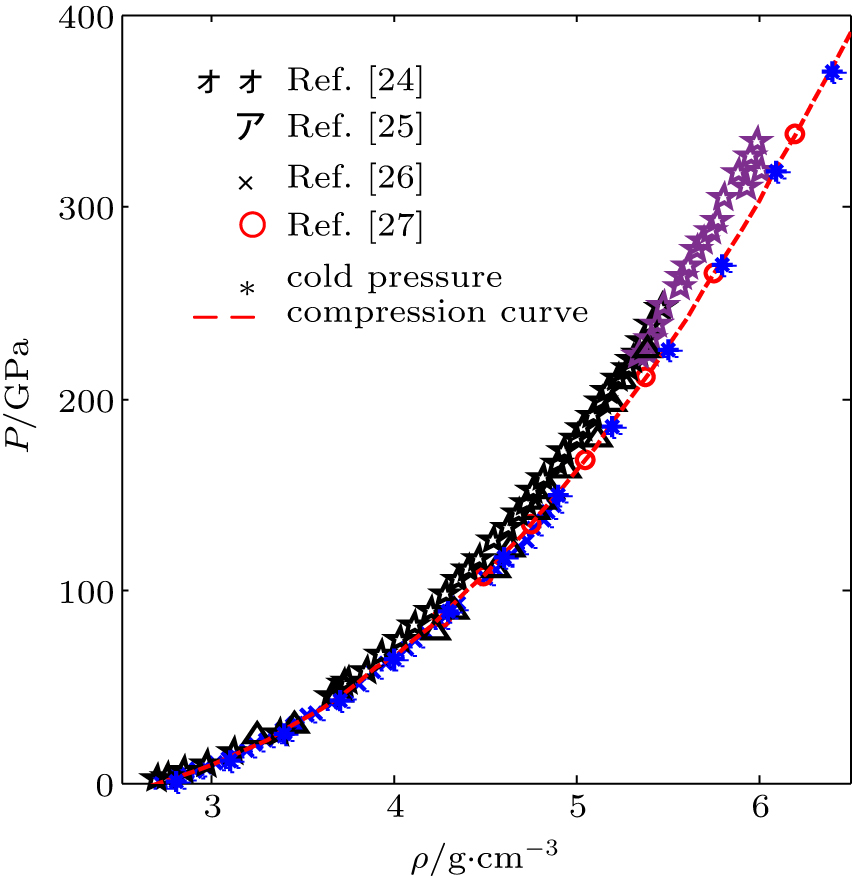	Fig. 2. The comparison of isothermal compression curve at ambient temperature with relevant experimental data and theoretical evaluation in compressed solid state.

The material behavior in condensed state at relatively high temperatures is one of the critical issues in EOS computations. The shock-compression experimental data is usually applied to verify the applicability of an EOS model in the region of high pressure and high temperature. If the shockwave propagates through a material, the thermodynamic parameter difference between the initial stage and behind the shockwave front is governed by the well-known Hugoniot relation^[28]

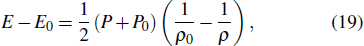The relation between pressure and density (or compression ratio) in Hugoniot curve can be calculated from Eq. (19) combined with the EOS model. The comparison of Hugoniot curve and relevant shock-compression experimental data^[29–33] and theoretical calculation^[34,35] is shown in Fig. 3. The Hugoniot curve is calculated up to the density of 10 g/cm³. It can be seen from Fig. 3 that the EOS predicts relatively accurate pressure along the Hugoniot curve with compression ratio ranging from 1 to 3.

Fig. 3.

	Figure Option ViewDownloadNew Window
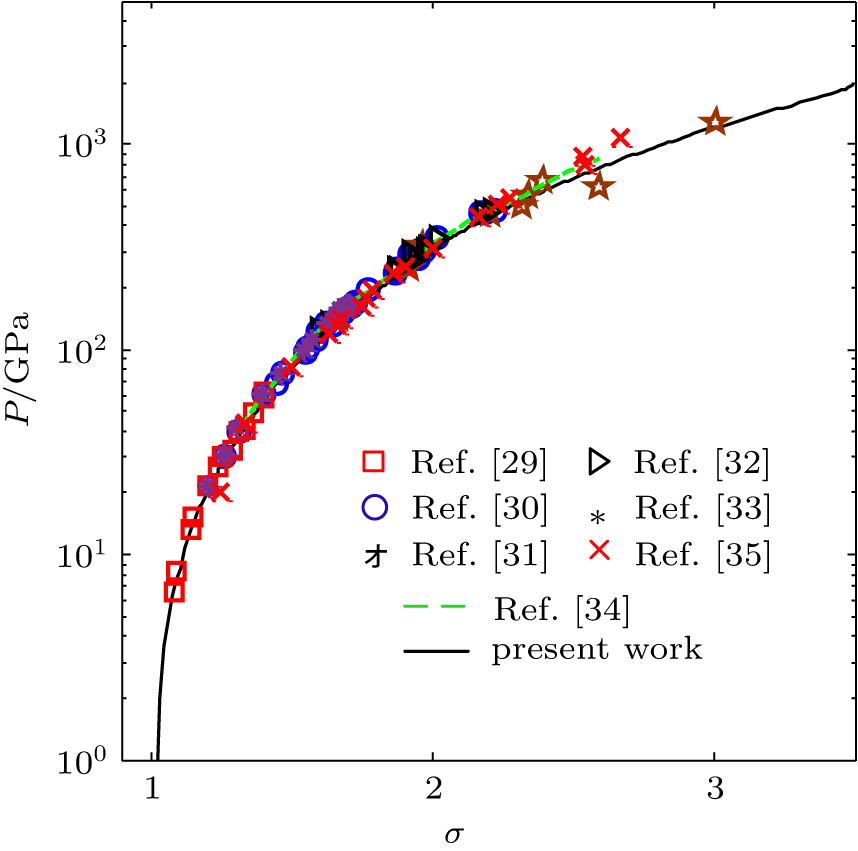	Fig. 3. Comparison of Hugoniot curve calculated by present EOS model with relevant shock-compression experimental data and theoretical evaluations.

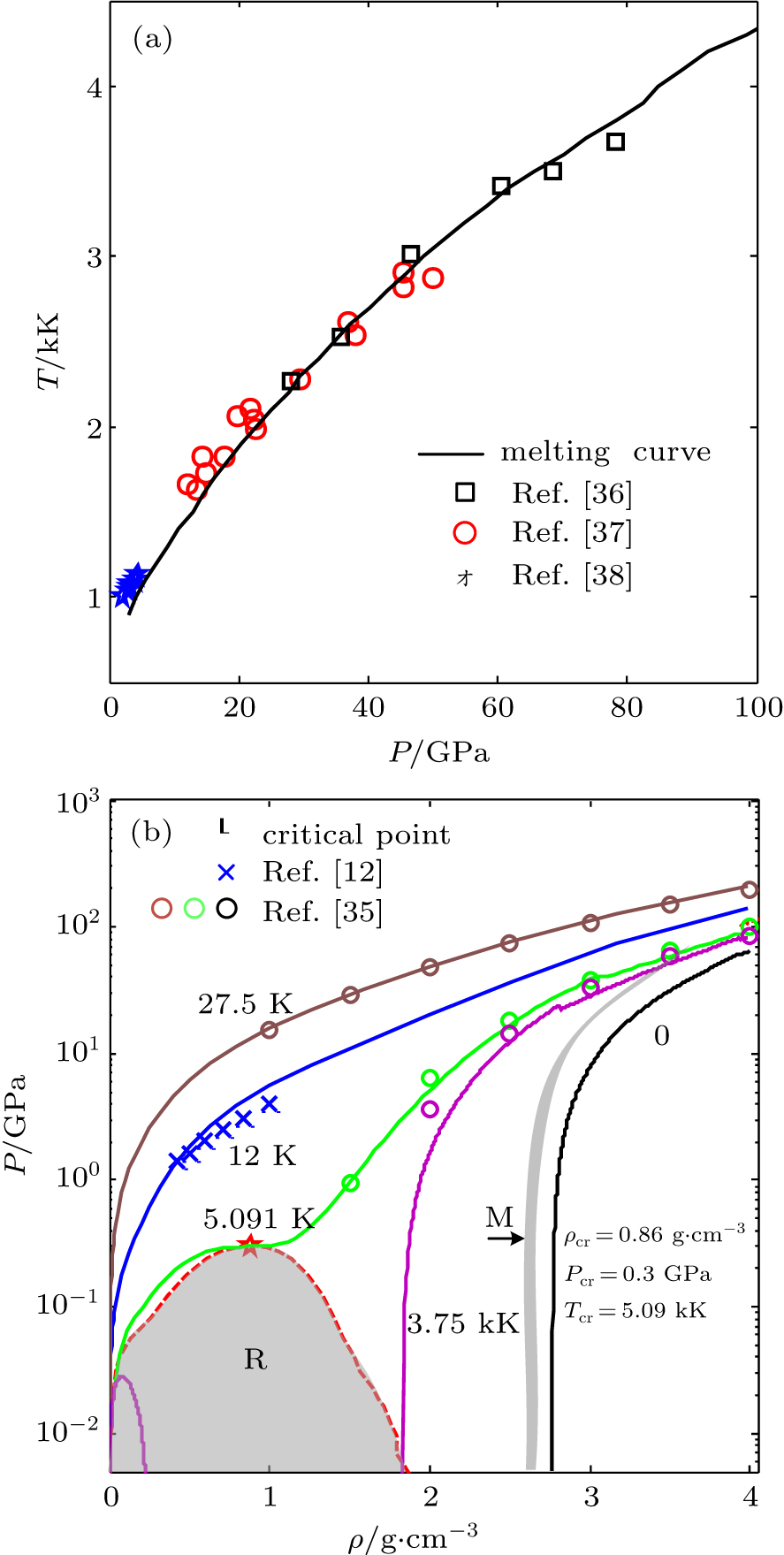
The metal material may experience severe phase transition from solid state to plasma state under the intense loading dynamics in warm dense matter regime. For instance, the thin aluminum wire is exploded into liquid, gas, and plasma states with pulsed current flowing through the load. The phase diagram is particularly important for analyzing the phase transition of the metallic target. The theoretical results of the phase diagram for aluminum calculated by the EOS model are shown in Fig. 4. The melting curve in Fig. 4(a) presents the dependence of melting temperature on pressure. The melting density and temperature are determined by the equivalence of free energy for solid and liquid states. It can be seen from the comparison between melting curve and experimental data^[36–38] in Fig. 4(a) that the calculated melting temperature in the region of low pressure is slightly lower than the experimental data, however, the relative error of the melting temperature is no more than 10%. The melting curve matches the experimental data very well in the relatively high-pressure region.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The theoretical calculation of phase diagram and comparison with relevant experimental data and theoretical evaluations: (a) melting curve at high pressures; (b) pressure–density phase diagram (solid line: isothermals for pressure; R: liquid–gas region; M: melting region; circle/cross: molecular dynamic simulations; red star: critical point).

Figure 4(b) shows the pressure–density phase diagram of aluminum, including the isothermals for pressure (solid line), liquid–gas region (grey region with red dashed line for liquid–gas coexistence curve), melting region (grey region with boundary of red dotted line), critical point (red star), and relevant molecular dynamic simulations (circle and cross marks).^[12,35] One can see from Fig. 4(b) that the isothermals for pressure are not monotonically increasing with density below the critical temperature, therefore, the saturated vapor pressure in liquid and gas phases at coexistence in the liquid–gas region can be calculated through Maxwell equal area rule. The branches for liquid and gas phases in coexistence curve connect at the critical point.

The parameters at the critical point are of great interest in many EOS computations. The critical density, temperature, and pressure are 0.86 g/cm³, 5.091 kK, and 0.3 GPa, respectively. A collection of estimated values of critical parameters for aluminum^[23,39,40] is presented in Table 2. The theoretical estimations for the critical parameters of aluminum from various EOS models exhibit relatively large variations. The critical temperature reported in many literatures ranges from 4.744 kK to 12.1 kK. The critical compressibility factor Z_c is usually used to compare the deviation of those critical parameters of different EOS models. The critical compressibility factor Z_c = 0.222 in the present work is close to the results derived by the soft-sphere model (Z_c = 0.243) and grand-canonical transition matrix Monte Carlo method (Z_c = 0.249).^[41]

Table 2.

Table 2.

Table 2. The collection of critical parameters for aluminum. . Tcr Pcr ρcr Zc Ref. 7.222 0.571 0.806 0.318 [11] 7.917 0.467 0.660 0.290 [23] 4.744−8.550 0.172−0.586 0.400−0.690 [39] 5.726 0.182 0.424 0.243 [40] 8.742 0.509 0.785 0.249 [41] 5.091 0.300 0.860 0.222 this work

Table 2. The collection of critical parameters for aluminum. .

The pressure and internal energy variation of aluminum at densities of 0.1 g/cm³ and 0.3 g/cm³ were measured using a homogeneous and thermally equilibrated plasma produced inside a closed vessel in the energy range 20–50 kJ/g by Renaudin^[1] and the isochore measurements were frequently used to verify the newly-established EOS models in warm dense matter regime. The pressure as a function of internal energy at densities of 0.1 g/cm³ and 0.3 g/cm³ derived from the present EOS model and comparison with experimental data are shown in Fig. 5. The theoretical results from QEOS, VASP calculated in Ref. [1] and results calculated by Lomonosov^[12] are also plotted in Fig. 5 for reference. One can see from Fig. 5 that the results from the present EOS model fit the experimental measurements relatively better among the theoretical models. The blue dashed line presents the results without practical modification of Eq. (18) to the pressure of the Thomas–Fermi–Kirzhnits model. The EOS model without pressure modification accords with experimental data at the density of 0.1 g/cm³, while generates noticeably lower pressure than experimental measurements at the density of 0.3 g/cm³. The value and variation trend in internal energy–pressure isochore curve of 0.3 g/cm³ is greatly improved with practical modification made to the Thomas–Fermi–Kirzhnits model.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The pressure as a function of internal energy at densities of 0.1 g/cm3 and 0.3 g/cm3 derived by the present EOS model and comparison with isochore measurements and other theoretical models.

A semi-empirical EOS model for aluminum in warm dense matter regime is constructed. The EOS model consists of three terms, i.e., the cold term, thermal contributions of ions and electrons. The Bush–Lomonosov model is used to estimate the cold term and thermal contribution of ions, while the thermal contribution of electrons is calculated based on the Thomas–Fermi–Kirzhnits model. The practical modifications are introduced to the Thomas–Fermi–Kirzhnits model to improve the prediction. The definition of applicable region of the Thomas–Fermi–Kirzhnits model from the condition of smallness of the corrections in comparison with thermodynamic parameter themselves is adopted to reshape the configuration of pressure. The minimum pressure for the thermal contribution of electrons is set to be zero artificially in the region where pressure depression from exchange and quantum corrections is larger than that derived from the Thomas–Fermi model. The critical parameters predicted by the EOS model are 0.86 g/cm³, 0.3 GPa, and 5.091 kK, respectively, giving a critical compressibility factor of 0.222. The isothermal compression curve, melting curve, and Hugoniot curve, as well as phase diagram are analyzed and compared with relevant experimental data and theoretical evaluations. The dependence of pressure on internal energy is verified by the isochore measurements in the warm dense matter regime. Generally speaking, the predictions of the EOS model are in relatively good agreement with the experimental data. This EOS model will be applied in the numerical investigation on the behavior of metallic target under the intense action of pulsed current in the future work, such as exploding wires and wire-array Z-pinch.