Formation mechanism of asymmetric breather and rogue waves in pair-transition-coupled nonlinear Schrödinger equations*

Project supported by the National Natural Science Foundation of China (Grant No. 61774001) and the Natural Science Foundation of Hunan Province, China (Grant No. 2017JJ2045).
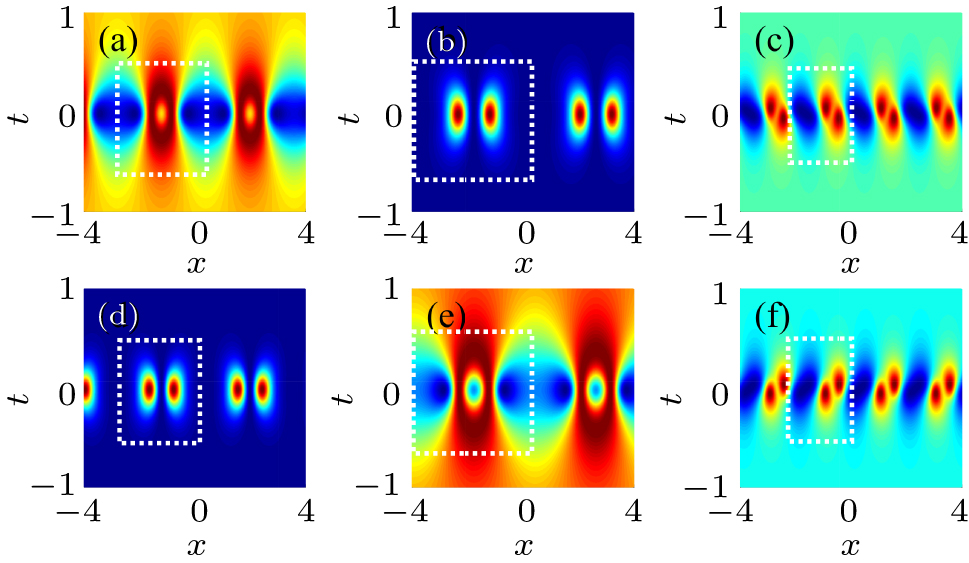
Li Zai-Dong1, 2, †, Wang Yang-yang1, He Peng-Bin3
       

The dynamic evolution of the Akhmediev breather solution in Eq. (6) with the parameters ν = 1, C1 = C3 = 1, C2 = 0, and C4 = 1.5. (a)–(c) Dynamic evolutions for the component |q1|2, and (d)–(f) dynamic evolutions for the component |q2|2. It can be seen that both (a) and (e) are dark Akhmediev breathers, both (b) and (d) are bright Akhmediev breathers, and (c) and (f) possess two peaks and one valley in each periodic unit. Other parameters are as follows: (a) and (d) a1 = 1.4, a2 = 0; (b) and (e) a1 = 0, a2 = 1.2277; (c) and (f) a1 = 1.4, a2 = 1.2277.