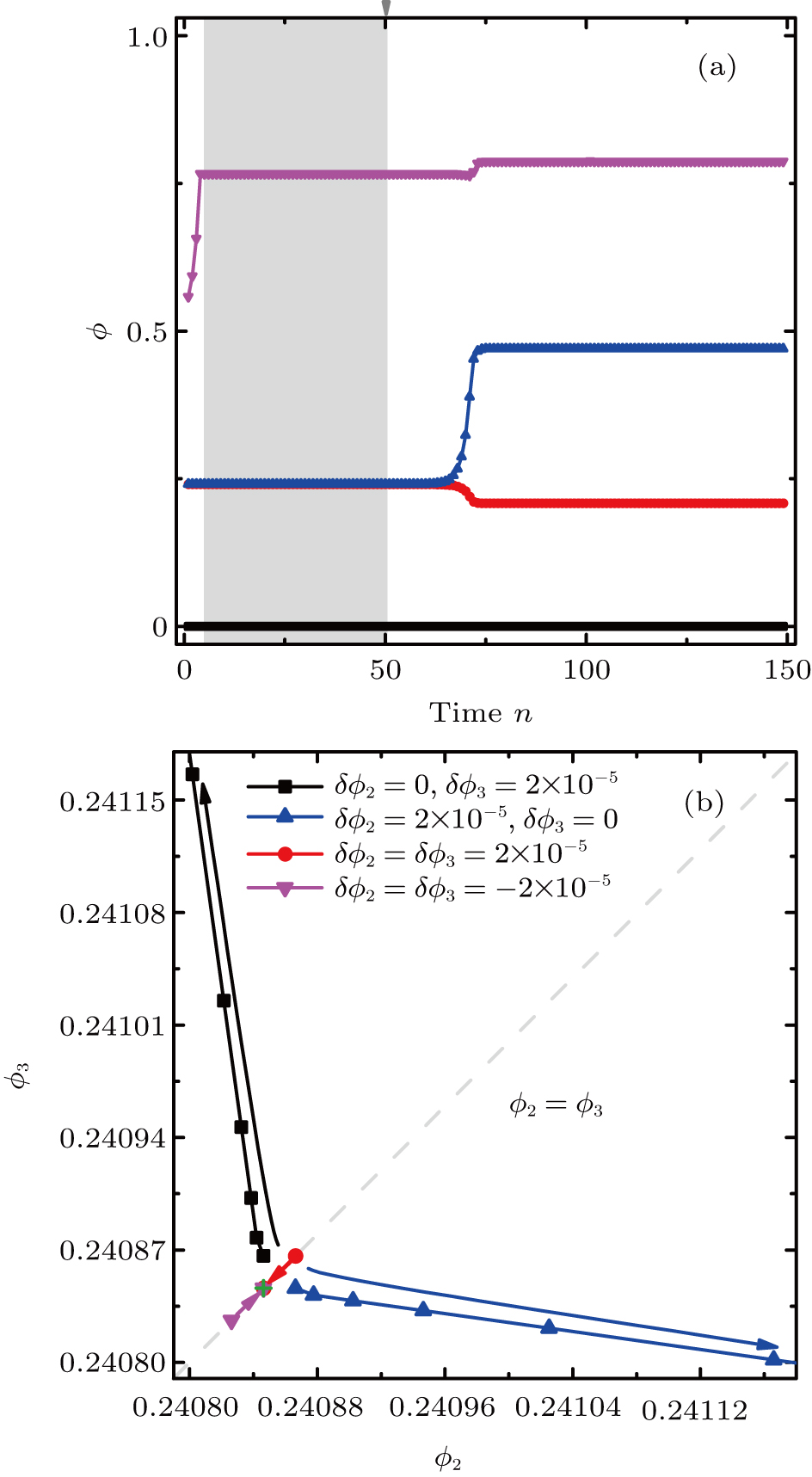
(a) An unstable attractor highlighted in gray is located with a randomly selected initial condition in four globally coupled oscillators. The four curves represent the states of the four oscillators respectively, which are recorded just after the n-th reset of the reference oscillator 1. Upon the perturbations introduced at the arrow position, the system will leave the attractor, indicating its unstable nature. (b) The dynamics in the (ϕ₂, ϕ₃) is shown, the existence of the two simultaneous active firing oscillators 2 and 3 is responsible for the unstable dynamics. The “+” denotes the unstable attractor. The different perturbations on oscillators 2 and 3 can split the simultaneous firing and make the system leave the unstable attractor (similar to the unstable manifold of a saddle). While the perturbations with δ ϕ₂ = δ ϕ₃ cannot split the simultaneous firings and the system can lead to the unstable attractor (similar to the stable manifold). The parameters are chosen as N = 4, b = 3, ε = 0.15, and τ = 0.2.