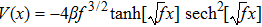Solitons in nonlinear systems and eigen-states in quantum wells*

Project supported by the National Natural Science Foundation of China (Grant No. 11775176), the Basic Research Program of Natural Science of Shaanxi Province, China (Grant No. 2018KJXX-094), the Key Innovative Research Team of Quantum Many-Body Theory and Quantum Control in Shaanxi Province, China (Grant No. 2017KCT-12), and the Major Basic Research Program of Natural Science of Shaanxi Province, China (Grant No. 2017ZDJC-32).
Zhao Li-Chen1, 2, †, Yang Zhan-Ying1, 2, Yang Wen-Li1, 2, 3
       

The profiles of quantum well which makes the Hamiltonian belong to the non-Hermitian Hamiltonian having parity–time symmetry. The quantum well admits the profile U ( x ) = − f sech 2 [ f x ] ( 2 β 2 f sech 2 [ f x ] + 1 ) and V ( x ) = − 4 β f 3 / 2 tanh [ f x ] sech 2 [ f x ] , for which it is hard to solve the Hamiltonian directly. But the corresponding eigen-state and eigenvalue can be obtained from the soliton solution of a nonlinear partial equation which can be solved by Darboux transformation. The parameters are β = 1 and f = 1.