Project supported by the National Key Research and Development Program of China (Grant No. 2016YFF0100501), the National Natural Science Foundation of China (Grant Nos. 61771466, 61775231, and 61611530708), the Six Talent Peaks Project of Jiangsu Province, China (Grant No. XXRJ-079), the Youth Innovation Promotion Association of Chinese Academy of Sciences (Grant No. 2017372), the Russian Foundation for Basic Research (Grant No. 17-52-53063), and the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20160400).
Project supported by the National Key Research and Development Program of China (Grant No. 2016YFF0100501), the National Natural Science Foundation of China (Grant Nos. 61771466, 61775231, and 61611530708), the Six Talent Peaks Project of Jiangsu Province, China (Grant No. XXRJ-079), the Youth Innovation Promotion Association of Chinese Academy of Sciences (Grant No. 2017372), the Russian Foundation for Basic Research (Grant No. 17-52-53063), and the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20160400).
† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant No. 2016YFF0100501), the National Natural Science Foundation of China (Grant Nos. 61771466, 61775231, and 61611530708), the Six Talent Peaks Project of Jiangsu Province, China (Grant No. XXRJ-079), the Youth Innovation Promotion Association of Chinese Academy of Sciences (Grant No. 2017372), the Russian Foundation for Basic Research (Grant No. 17-52-53063), and the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20160400).
Antenna-coupled field-effect-transistors (FETs) offer high sensitivity for terahertz detection. Both the magnitude and the polarity of the response signal are sensitive to the localized terahertz field under the gate. The ability of accurate sensing the intensity pattern is required for terahertz imaging systems. Here, we report artefacts in the intensity pattern of a focused terahertz beam around 1 THz by scanning a silicon-lens and antenna coupled AlGaN/GaN high-electron-mobility-transistor (HEMT) detector. The origin of the image distortion is found to be connected with one of the antenna blocks by probing the localized photocurrents as a function of the beam location and the frequency. Although the exact distortion is found with our specific antenna design, we believe similar artefacts could be commonplace in antenna-coupled FET terahertz detectors when the beam spot becomes comparable with the antenna size. To eliminate such artefacts, new antenna designs are welcomed to achieve strong asymmetry in the terahertz field distribution under the gate while maintaining a more symmetric radiation pattern for the whole antenna.
Sensitive terahertz sensors are one of the key devices in terahertz application systems, for example, terahertz imagers and scanners.[1–8] Such systems usually require direct detection of the terahertz power,[9] while some other systems, for example, coherent sensing systems need detection of phase as well.[10–12] Terahertz detectors and array for imaging applications require a precise response to the spatially distributed terahertz power of the incoming terahertz wave. An antenna-coupled field-effect-transistor (FET) terahertz detector receives the incident terahertz wave by the integrated onchip antenna and generates a self-mixing current. Since it is the asymmetry that ensures the generation of an unidirectional self-mixing current,[13–16] an asymmetric antenna is required to make the self-mixing more effective. For this purpose, a few different types of antennas or couplers have been realized and examined in FET-based detectors.[17–23] Recently, Boppel et al. found that an FET detector coupled with symmetric antennas is able to detect the intensity gradient and hence allows for direct edge detection.[14] They further pointed out that the asymmetry in the antenna-coupled FETs has to be assured so that the devices can be used as pure power detectors and become insensitive to the intensity gradient. For sensing and imaging applications, silicon lenses are widely used to greatly improve the coupling efficiency and hence the sensitivity by focusing the terahertz wave onto the active regions of the detectors.[23–25] Unlike optoelectronic detectors for shorter wavelength radiation in which the dimension of the detector area is greater than the wavelength, the integration of FET detectors with silicon lenses may induces a beam spot size comparable to the antenna. The detector response becomes sensitive to the location of the focused beam relative to the antenna and gives rise to unpredicted changes not only in the magnitude but also in the photocurrent direction in some circumstances. Hence, careful design of the antenna and accurate alignment of the antenna to the silicon lens are needed to avoid unwanted artefacts in the terahertz imaging system. In this work, we report raster scanned images of a focused terahertz beam by using an antenna-coupled highelectron- mobility-transistor (HEMT) detector integrated on a silicon lens. An image distortion is found to be related with the frequency and the relative location between the focused beam and the antenna. Possible solutions to eliminate this type of artefacts are discussed.
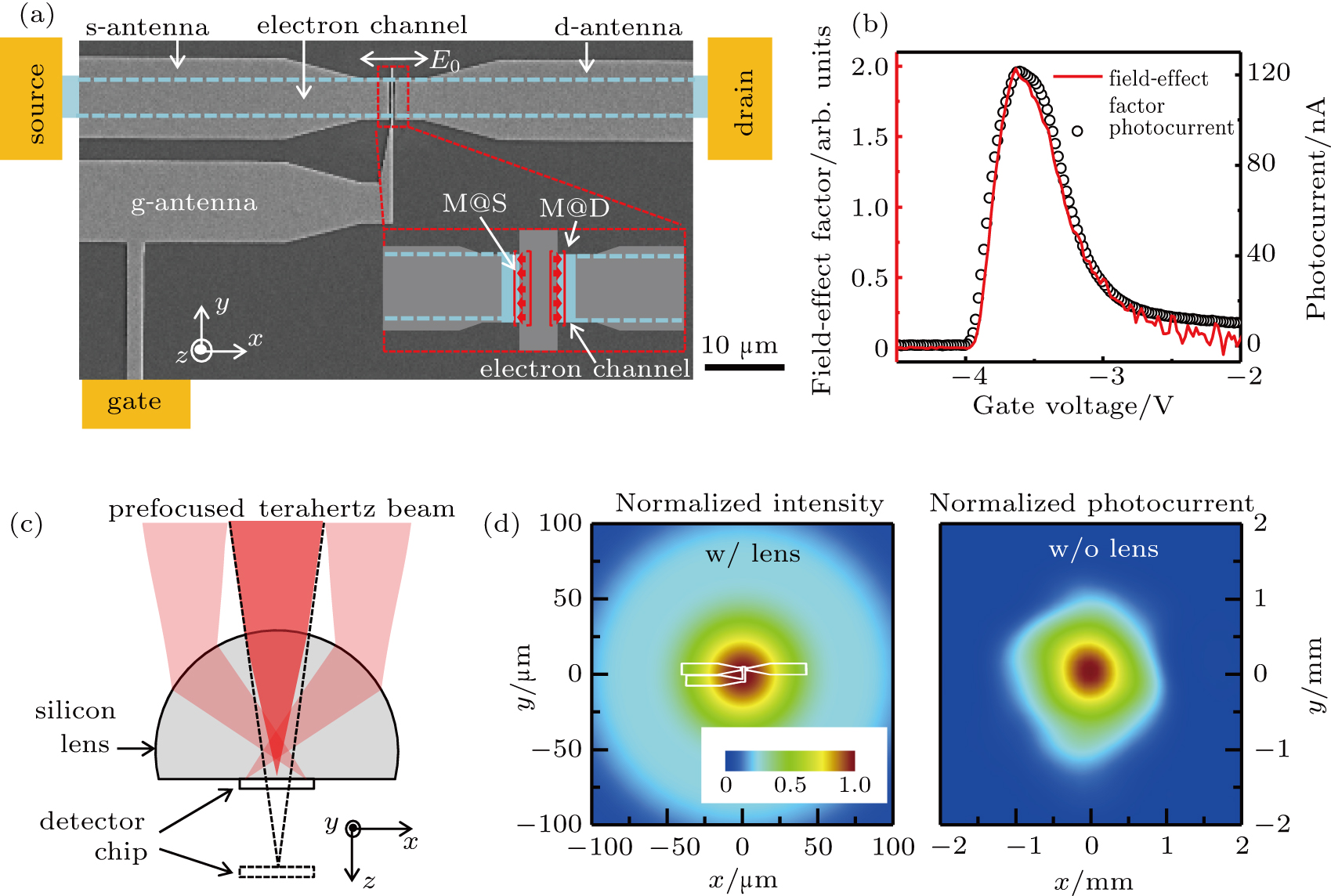
The terahertz detector is an antenna-coupled HEMT fabricated based on AlGaN/GaN heterostructure with a sapphire substrate. The fabrication process has been introduced in details in our previous reports.[15,26] As shown in Fig.
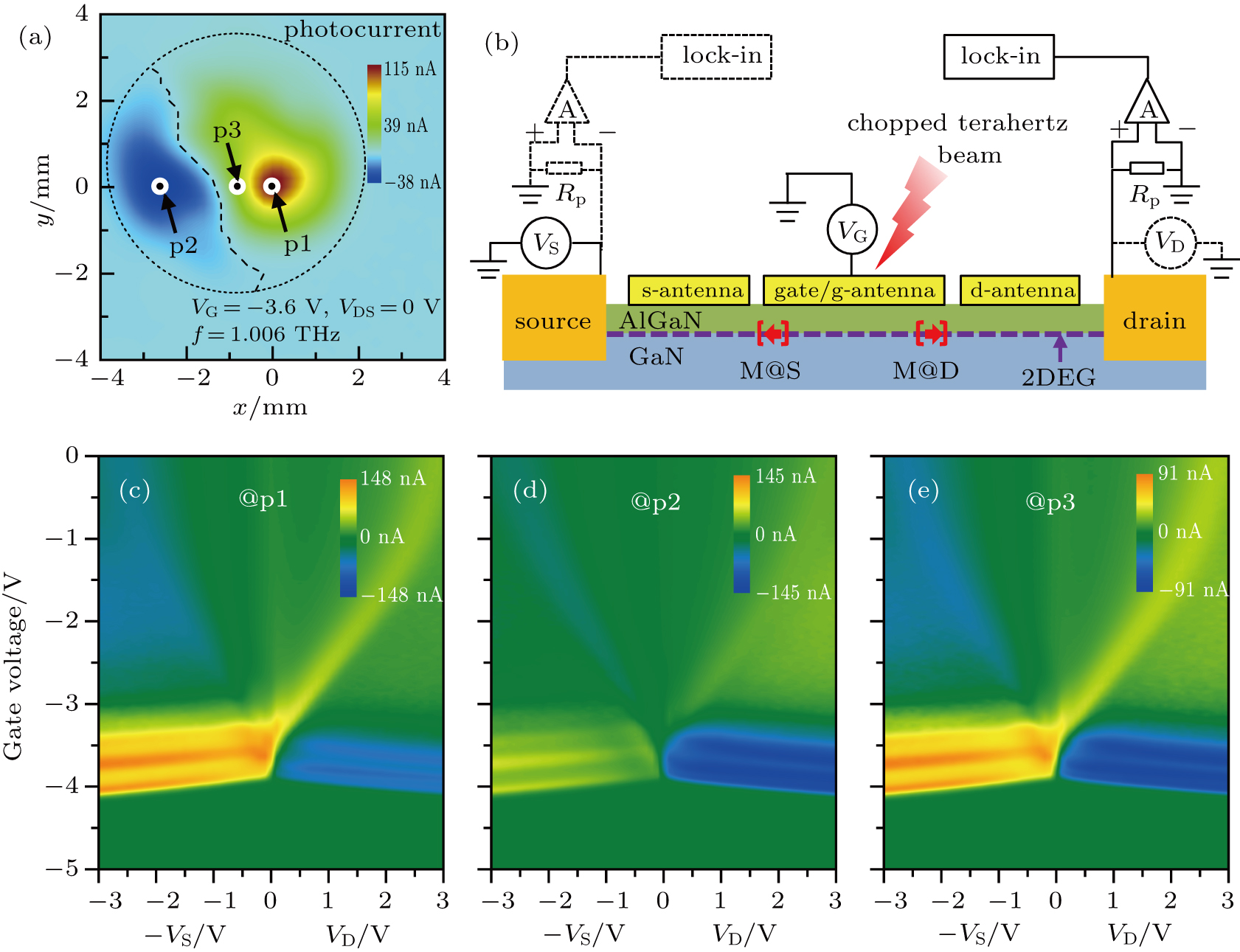
As reported earlier in Ref. [26], the terahertz detector consists of the terahertz antenna and the HEMT. The incident terahertz beam reaches the channel of the HEMT, after collected by the terahertz antenna, induces an electric field in the channel. There exist two terahertz field components (Ex and Ez) in the gated electron channel, one alone direction x, i.e., from source to drain, the other in z, i.e., perpendicular to the plane of the channel. The self-mixing current generated in M@S or M@D is proportional to the product of the two field components. Due to the phase change of π between field components Ez in areas M@S and M@D, a negative self-mixing current and a positive self-mixing current are generated in areas M@S and M@D, respectively, as schematically illustrated by the red arrows in brackets in Fig. 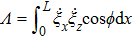
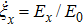

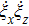
Attempts to enhance the photocurrent include increase of the field-effect factor, increase of the terahertz field strength in one of the mixing areas, and increase of the degree of asymmetry in the field distribution. In our specific antenna design, since the strength of the mixing factor in M@S is about one third of that in M@D, there is a significant fraction of mixing current in M@D which is compensated by the opposite current in M@S.[15] When the terahertz beam is focused down to a diameter about 1 mm by using a three-inch-diameter offaxis parabolic (OAP) mirror, no negative photocurrent can be probed in such detector without silicon lens. However, a negative photocurrent can be extracted from such bare detectors even without silicon lens by applying a positive source–drain bias on the drain to deplete the electron channel and hence suppress the positive self-mixing current in M@D.[26] In this work, the terahertz beam before the silicon lens is prefocused by an OAP mirror and the detector is mounted in the center of a hyperspherical silicon lens with a diameter of 6 mm, as schematically shown in Fig.
By applying a gate voltage of −3.6 V and a zero source–drain bias, the lens-integrated detector is used to scan the prefocused terahertz beam at 1.006 THz. The obtained image of the photocurrent is shown in Fig.
As shown in Fig.
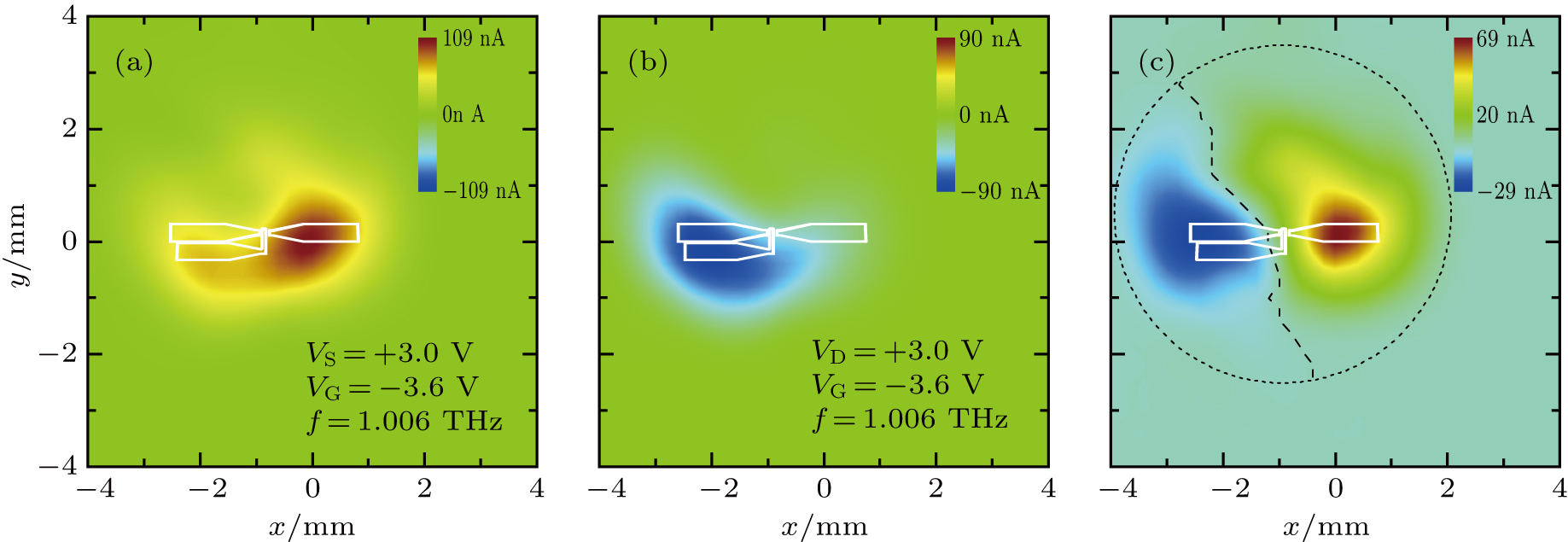
The local self-mixing in M@S and M@D can be effectively switched off by depleting the corresponding electron channel. We examine the images of the same focused beam by applying a +3.0 V bias to the source or the drain, as shown in Figs.
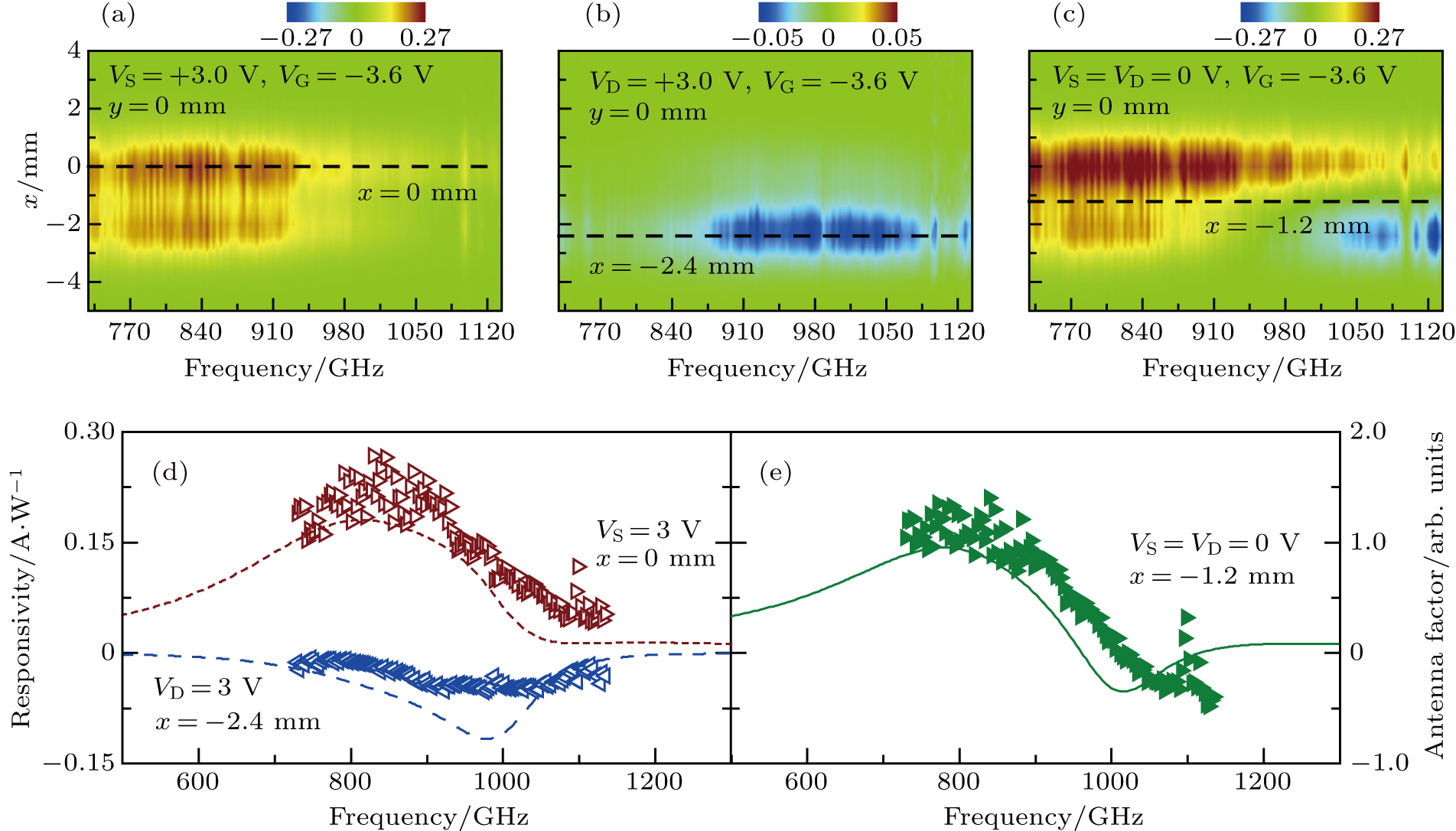
The effect of the three-block antenna and the interplay of the local self-mixing currents in M@S and M@D can also be seen when the frequency is swept. To reveal the frequency response, the detector responsivity is obtained by normalizing the photocurrent with the corresponding terahertz power. With a +3 V bias applied on the source, the responsivity as a function of the frequency and the location in x is plotted in Fig.
FET-based terahertz detectors require an inherently asymmetric field distribution under the gate. In our specific three-block antenna design, the asymmetric field distribution is assured by d-antenna and g-antenna. The addition of s-antenna introduces an extra antenna mode which is responsible to the negative photocurrent generated in M@S. When the detector is integrated on a hyperspherical silicon lens, the focused beam spot has a dimension comparable to the antenna size, severe image distortion appears due to the interplay of d-antenna and s-antenna. Although the negative photocurrent can be effectively suppressed by an external positive bias applied on the source, the intensity pattern scanned by the lens-coupled detector exhibits strong dependence on the geometric configuration of the antenna and the lens. Hence, a new antenna design enabling an asymmetric field distribution under the gate while maintaining a symmetric radiation pattern is preferred for power detection and imaging. The following procedures could be taken: 1) remove s-antenna and duplicate g-antenna on the other side of the channel to make a new three-block antenna with higher symmetry in the radiation pattern; 2) replace the hyperspherical lens with a hemispherical or hypo-hemispherical lens so as to make the beam spot slightly larger than the antenna size; 3) bias the detector to suppress the unwanted part of the self-mixing currents. Also, methods of calibrating such integrated detectors should be developed to evaluate the performance in recovering the true intensity pattern of an arbitrary incoming terahertz beam.
The photoresponse of an antenna-coupled AlGaN/GaN-HEMT terahertz detector integrated on a silicon lens was examined to reveal the effect of the antenna irradiated by a focused terahertz beam. The integrated detector is sensitive to the location of the incident terahertz wave and does not reflect the intensity pattern truthfully. The s-antenna is found to be responsible to the distortion in intensity pattern. Such artefacts might be commonplace in antenna-coupled FET terahertz detectors especially when the terahertz beam is strongly focused with a dimension comparable to the antenna size. Precautions have to be taken when such detectors are used for imaging. Such artefacts are expected to be eliminated by improving the symmetry in the antenna’s radiation pattern while maintaining the strong asymmetry in the terahertz field distribution under the field-effect gate.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] |