Project supported by the National Natural Science Foundation of China (Grant Nos. 11474308, 11574343, and 11774377).
Project supported by the National Natural Science Foundation of China (Grant Nos. 11474308, 11574343, and 11774377).
† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11474308, 11574343, and 11774377).
Ultrasonic inspection of austenitic steel weld is a great challenge due to skewed and distorted beam in such a highly anisotropic and inhomogeneous material. To improve the ultrasonic measurement in this situation, it is essential to have an in-depth understanding of ultrasound characteristics in austenitic steel weld. To meet such a need, in the present study we propose a method which combines the weld model, Dijkstra’s path-finding algorithm and Gaussian beam equivalent point source model to calculate the acoustic fields from ultrasonic phased array in such a weld. With this method, the acoustic field in a steel-austenitic weld-steel three-layered structure for a linear phase array transducer is calculated and the propagation characteristics of ultrasound in weld are studied. The research results show that the method proposed here is capable of calculating the acoustic field in austenitic weld. Additionally, beam steering and focusing can be still realized in the austenitic steel weld and the beam distortion is more severe in the middle of weld than at other positions.
Austenitic steel, as a kind of specific complex material, is welded widely in nuclear power plants and other industries.[1–5] For security reasons, it is of great importance to evaluate the structural integrity of the austenitic steel weld. However, due to the high anisotropy and inhomogeneity, huge difficulties exist when using ultrasound technique to inspect such a structure. Apart from the energy attenuation, the elastic wave will be spited and skewed, which makes the testing results inaccurate. As a result, developing a method to evaluate the acoustic fields inside austenitic steel weld has become an urgent need.
Up to now, a lot of efforts have been made by numerous researchers. Silk[6] first developed a computer model based on ray tracing technique to predict the ray paths in complex orthotropic structures. Ogilvy[7,8] presented a weld model to approximately describe the grain orientation at each position and developed the RAYTRAIM, a commercial software package, based on weld model and traditional ray tracing technique. Spies[9] calculated the acoustic fields emitted from a single transducer in multilayered inhomogeneous anisotropic medium and austenitic steel weld respectively by using multi-Gaussian beam (MGB) model. Ye et al.[10] presented a model combining the traditional ray tracing technique and the linear phasing multi-Gaussian beam model to calculate the focused fields produced by a phased array transducer in dissimilar metal welds. Kolkoori et al.[11] introduced the ray directivity factor into ray tracing technique and calculated the acoustic fields in specific directions from distributed sources in austenitic steel weld. Simulation results were validated with the results obtained from two-dimensional (2D) elastodynamic finite integration technique (EFIT) and experiments. Although the traditional ray tracing technique is a powerful tool for determining the ray path, it must be run many times if the number of target points is large, which will increase the computation time. In such a situation, Nowers Oliver et al.[12,13] first adopted the Dijkstra’s algorithm and A* algorithm which have been widely used in computer science for finding the shortest path to predict the ray paths in austenitic steel welds efficiently. And, it is worth mentioning that the Dijkstra’s algorithm,[14] as a novel ray tracing technique, can be used to obtain the ray paths from one source to any number of target points in one run. However, such an algorithm can only be used to determine the ray path but not to calculate the amplitude of acoustic field.
For the calculation of acoustic fields in frequency domain, the multi-Gaussian beam (MGB) model, based on the superposition of several (10–15) special Gaussian beams, has been widely used by numerous researchers[15–19] and considered as the most efficient method, especially in multiple medium. However, due to the assumption of paraxial approximation, when it comes to phased array, this method will lose accuracy if the steering angle becomes too large.[20] For this reason, some efforts have been made to solve this problem. Zhao[21,22] expressed the distance factor in terms of several approximate terms and proposed a nonparaxial multi-Gaussian beam model. Huang[23–25] introduced 2 modification factors into the MGB model including linear phasing and directivity function and developed the LPMGB model. Furthermore, Schmerr[15] combined the point source superposition model and Gaussian beam method, and finally developed the Gaussian beam equivalent point source (GBEPS) model. In this model, the surface of each transducer is considered as the superposition of several point sources and each point source emits spherical wave into medium. Through substituting a specific Gaussian beam for spherical wave and rotating the coordinate system to make each field point be on the main axis of Gaussian beam, the limitation of paraxial approximation can be eliminated. In view of this, the GBEPS model is used here to simulate the acoustic fields emitted by ultrasonic phased array in austenitic steel weld.
Therefore, in this work, for evaluating the acoustic field in weld, a systematic method combining with the weld model for describing grain orientation inside austenitic steel weld, the Dijkstra’s algorithm for obtaining ray paths, and the Gaussian beam equivalent point source (GBEPS) model[15] for calculating the amplitude of displacement is introduced and discussed. In addition, as a simulation example, the case of steel-weld-steel with linear phased array transducer is considered and the focusing and steering fields are calculated and analyzed by using the proposed approach.
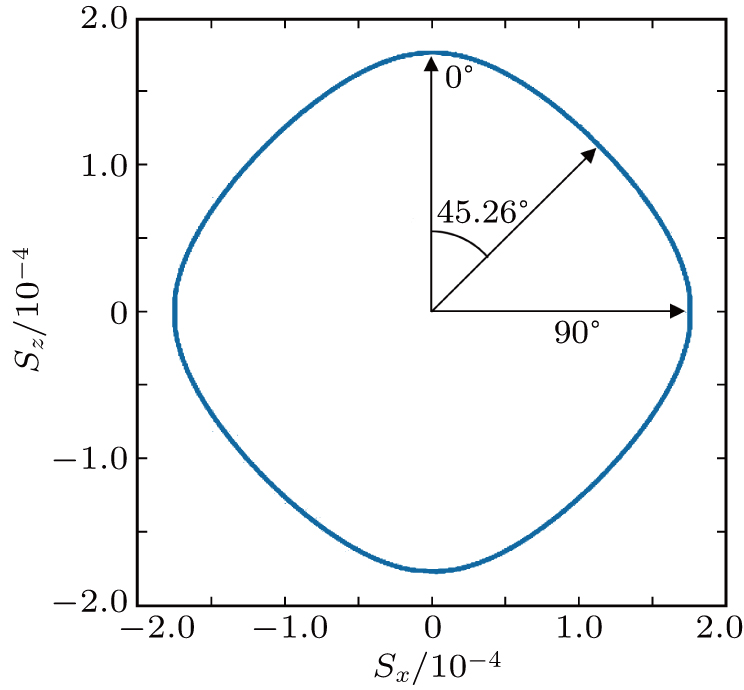
Generally, the austenitic steel weld is a kind of anisotropic and inhomogeneous material. In the formation of the weld, crystalline grains grow along the maximum thermal gradient when cooling,[3] which causes the coarse grains with different orientations: such a formation process is different from that of isotropic material. As a result, while traveling through such a material, the ultrasound will be steered and distorted by these grains, which means that the determination of grain orientations plays an important role in studying the propagation of ultrasound in austenitic steel weld. In this paper, the weld model presented by Ogilvy[7] is adopted, which gives a mathematical empirical function to describe the local grain orientations of the weld. The form of function is given as
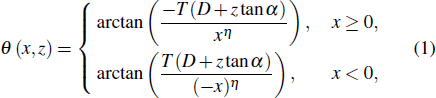 |
Figure
As a matter of fact, the phase velocity c is generally different from group velocity
 |
| Table 1. Material properties for transversely isotropic type-316 austenitic steel weld metal. . |
Figure
Consider a linear phased array with N elements. Each element is divided into Q segments which are tiny enough to be regarded as point sources emitting spherical wave. According to the GBEPS model, such a spherical wave at each field point is approximated as a specific Gaussian beam. And the particle velocity in the M + 1 medium,
 |
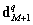
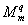
From Eq. (
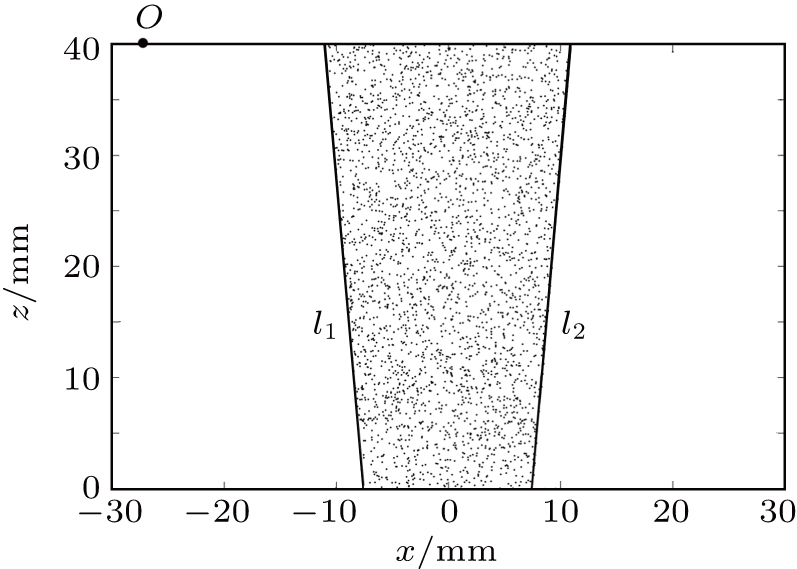
According to the Dijkstra’s algorithm, a large number of nodes are distributed randomly in the austenitic weld and on the interfaces (l1 and l2) (Fig.
(i) Choose a current node N1 on the interface l1 [Fig.
(ii) With the known grain orientations at these adjacent nodes, calculate the phased velocity and group velocity corresponding to the propagation directions from N1 to them. And then, the propagation time of group velocity can be obtained., on the assumption that the materials between N1 and its adjacent nodes are homogeneous anisotropic medium.
(iii) Find the node N2 which has the shortest propagation time and define it as the new current node [Fig.
(iv) Calculate the vector of virtual boundary L2 at current node N2 using Eq. (
(v) Calculate the incident, refracted angle θ2i, θ2t, and transmission coefficient T2 at N2.
(vi) Using Eq. (
(vii) Repeat Steps (iv)–(vi) until all of nodes in weld are calculated.
After the above algorithm is done, the acoustic fields of all the nodes in the weld, generated by one element of transducer, are calculated. When the phased array transducer with N elements is used, the acoustic fields can be calculated by superposing the results from all elements with proper time delay, which is expressed by
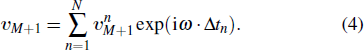 |
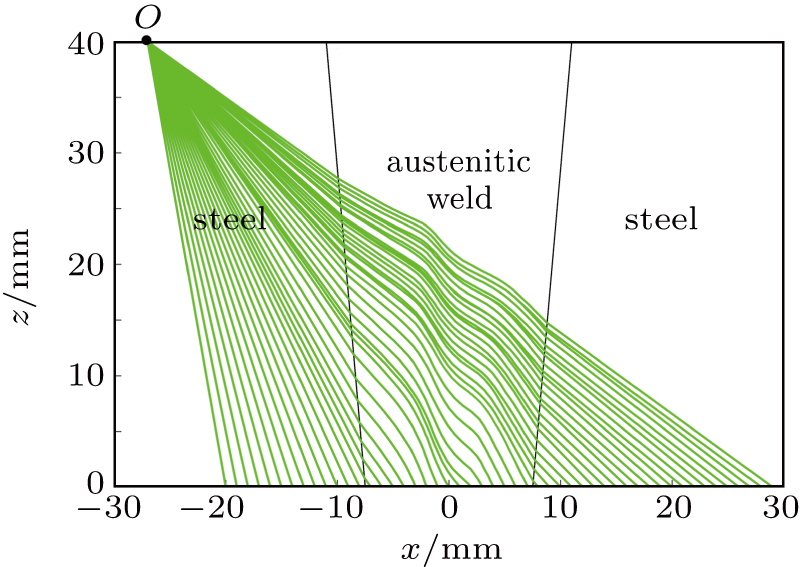
To demonstrate the presented method, the radiated acoustic fields emitted by a linear phased array transducer in steel-austenitic steel weld-steel structure [Fig.
Figure
Figures
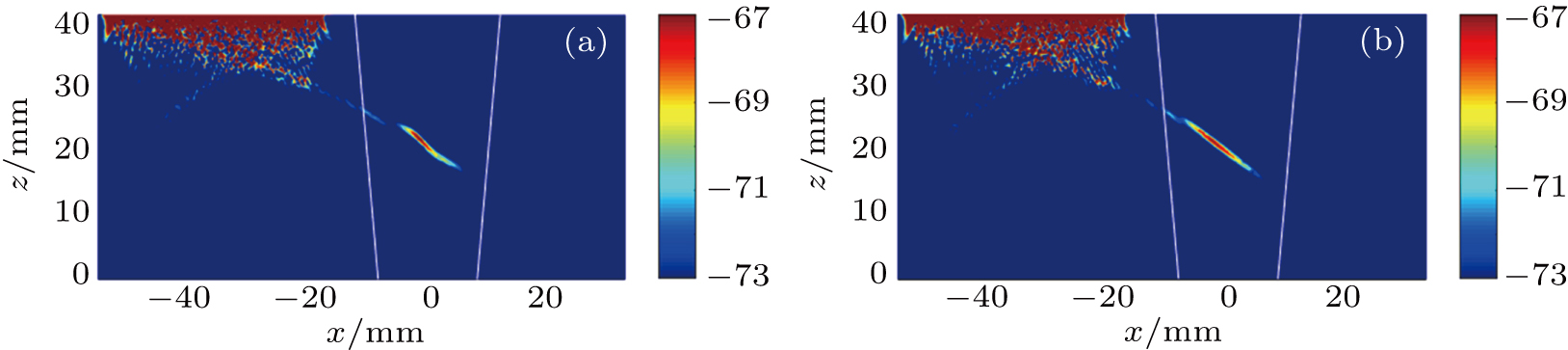
To make acoustic wave focus at a specific point, time delays of all elements should be obtained at first by using Dijkstra’s algorithm. Figure
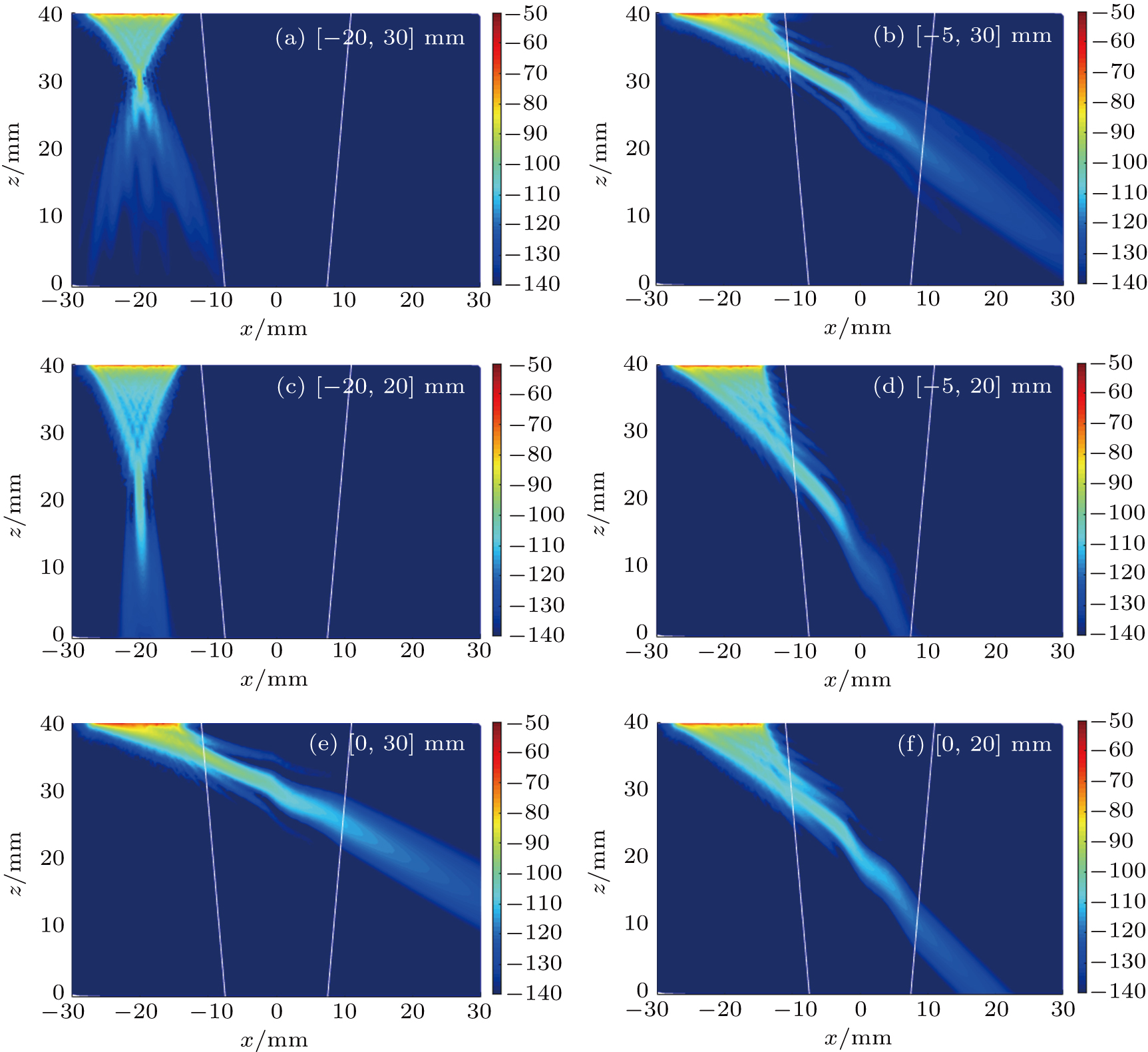 | Fig. 7. Acoustic fields focused at several points: (a) [−20, 30] mm, (b) [−5, 30] mm, (c) [−20, 20] mm, (d) [−5, 20] mm, (e) [0, 30] mm, (f) [0, 20] mm. |
At present, during setting the detection parameters and image processing, the ultrasonic detection of welds is still generally based on the weld model under the assumption of isotropic medium. In practice, however, the propagation path of sound wave in the real austenitic stainless steel welds is deflected and bent as shown in Figs.
Firstly, for a real austenitic stainless steel weld, if the isotropic medium model is used to simplify the calculation, the ray paths and time delays of phased array will be obtained easily, but the actual acoustic beam cannot accurately focus on the target point. Figure
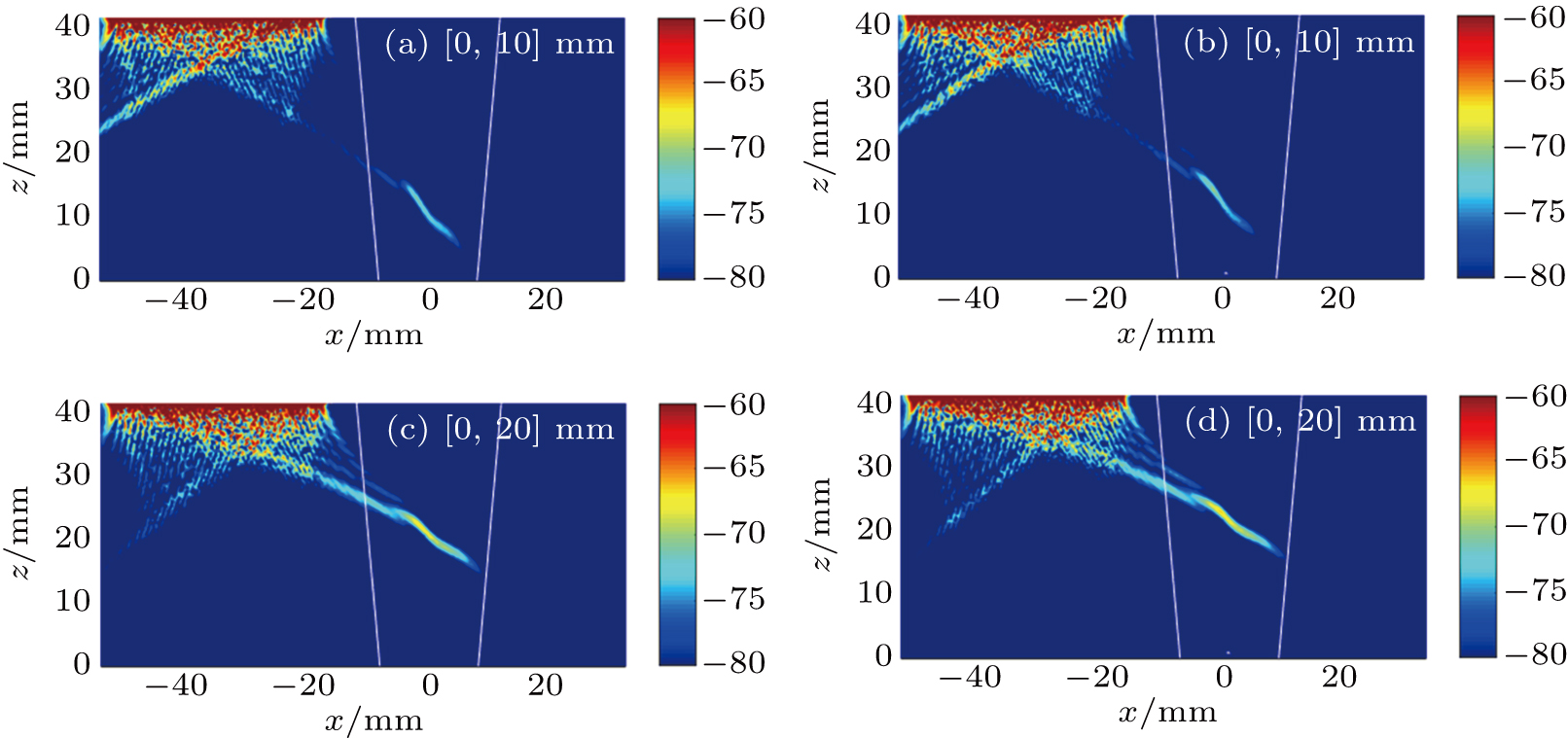 | Fig. 8. Comparison among focused sound fields in anisotropic weld model (Ogilvy) under different delay rules. Delays are calculated by using ((a), (c)) proposed method and ((b), (d)) isotropic model. |
In addition, in the process of defect imaging, such as time reversal focusing imaging, the actual delayed echo data are affected by the inhomogeneous anisotropy of weld, but such an effect cannot be reconstructed in the isotropic medium model, which will lead to inaccurate defect imaging results. At this time, more accurate weld simulation model is needed to reconstruct the echo data, and the model and algorithm proposed here can be used to improve the imaging accuracy. Figure
A systematic method combining with weld model, Dijkstra’s algorithm and Gaussian beam equivalent point source model is presented and allows the calculation of acoustic fields generated by phased array transducer in austenitic steel weld. As a simulation example, the case of steel-austenitic steel weld-steel with linear phased array is considered, in which, the longitudinal acoustic fields with different time delays are calculated and beam steering and focusing are realized. As the example illustrates, useful information including ray path, particle velocity amplitude and propagation characteristics in austenitic steel weld can be obtained, which demonstrates the capability of the proposed method. Simulation results show the propagation behavior of ultrasound through austenitic steel weld and also indicate that the ultrasound is distorted and skewed severely in the middle of the weld. Finally, the problems that may be caused by the isotropic theory in the actual austenitic weld inspection are analyzed. These results present theoretical support for actual ultrasound testing.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] |