Project supported by the National Key Research and Development Program of China (Grant Nos. 2018YFA0306600 and 2016YFB0501603), the National Natural Science Foundation of China (Grant No. 11761131011), the Fund from the Chinese Academy of Sciences (Grant Nos. GJJSTD20170001, QYZDYSSWSLH004, and QYZDB-SSW-SLH005), the Anhui Initiative Fund in Quantum Information Technologies, China (Grant No. AHY050000), and the Youth Innovation Promotion Association of the Chinese Academy of Sciences.
Project supported by the National Key Research and Development Program of China (Grant Nos. 2018YFA0306600 and 2016YFB0501603), the National Natural Science Foundation of China (Grant No. 11761131011), the Fund from the Chinese Academy of Sciences (Grant Nos. GJJSTD20170001, QYZDYSSWSLH004, and QYZDB-SSW-SLH005), the Anhui Initiative Fund in Quantum Information Technologies, China (Grant No. AHY050000), and the Youth Innovation Promotion Association of the Chinese Academy of Sciences.
† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant Nos. 2018YFA0306600 and 2016YFB0501603), the National Natural Science Foundation of China (Grant No. 11761131011), the Fund from the Chinese Academy of Sciences (Grant Nos. GJJSTD20170001, QYZDYSSWSLH004, and QYZDB-SSW-SLH005), the Anhui Initiative Fund in Quantum Information Technologies, China (Grant No. AHY050000), and the Youth Innovation Promotion Association of the Chinese Academy of Sciences.
There are some problems that quantum computers seem to be exponentially faster than classical computers, like factoring large numbers, machine learning, and simulation of quantum systems. Constructing an appropriate quantum algorithm becomes more important for solving these specific problems. In principle, any quantum algorithm can recast by a quantum random walk algorithm. Although quantum random walk with a few qubits has been implemented in a variety of systems, the experimental demonstration of solid-state quantum random walk remains elusive. Here we report the experimental implementation of the quantum continuous-time random walk algorithm by a two-qubit quantum processor in a nitrogen–vacancy center in diamond. We found that quantum random walk on a circle does not converge to any stationary distribution and exhibit a reversible property. Our results represent a further investigation of quantum walking dynamics in solid spin platforms, may also lead to other practical applications by the use of quantum continuous-time random walk for quantum algorithm design and quantum coherence transport.
Richard Feynman[1] proposed the idea of quantum computing for the first time in 1982. He believes that computers built according to the principles of quantum mechanics are more efficient than classical computers in dealing with a certain type of problem. Only at the end of the 20th century, Deutsch[2] and Shor[3] discovered the first two famous quantum algorithms and since then the research of quantum computing has been developed more rapidly. Creating an efficient quantum algorithm plays a crucial role in the manufacture of the quantum computer. Unfortunately, finding a new quantum algorithm is a challenging task.
Quantum random walk (QRW) is a fundamental model of dynamical process and has extensive application in science, such as fast hitting tasks[4] and energy transport simulation.[5] In the quantum regime, quantum state has the characteristics of quantum superposition and quantum coherence. Therefore, QRW shows different behaviors from its classic version.[6,7] These characteristics allow QRW to simulate large-scale quantum many-body systems and realize universal quantum computation without time-dependent control.[8] For instance, some theoretical researchers have been revealed that QRWs propagating in one dimension (1D) have better transmission characteristics than 1D classical random walks.[9] A dozen years ago, a quantum search algorithm, which is based on the framework of QRW algorithm with remarkable speed up to their corresponding classical algorithm, was reported in Ref. [10]. Some researchers showed that in principle, any quantum algorithm can be recast as a quantum walk algorithm.[11] QRWs have been successfully implemented in systems as diverse as NMR,[12,13] bulk,[14] and fibre[15] optics, trapped ions,[16,17] trapped neutral atoms,[18] superconducting qubits,[8] and photonics.[19–22]
Here, we report an experimental realization of the quantum continuous-time random walk (CTRW) algorithm in the nitrogen-vacancy (NV) center in diamond by a two-qubit programmable quantum processor. We found that QRW has completely different probability distributions from classical random walk. While the probability distributions of the classic CTRW exhibit a uniform distribution, the probability distributions of the quantum CTRW show an oscillating trend.
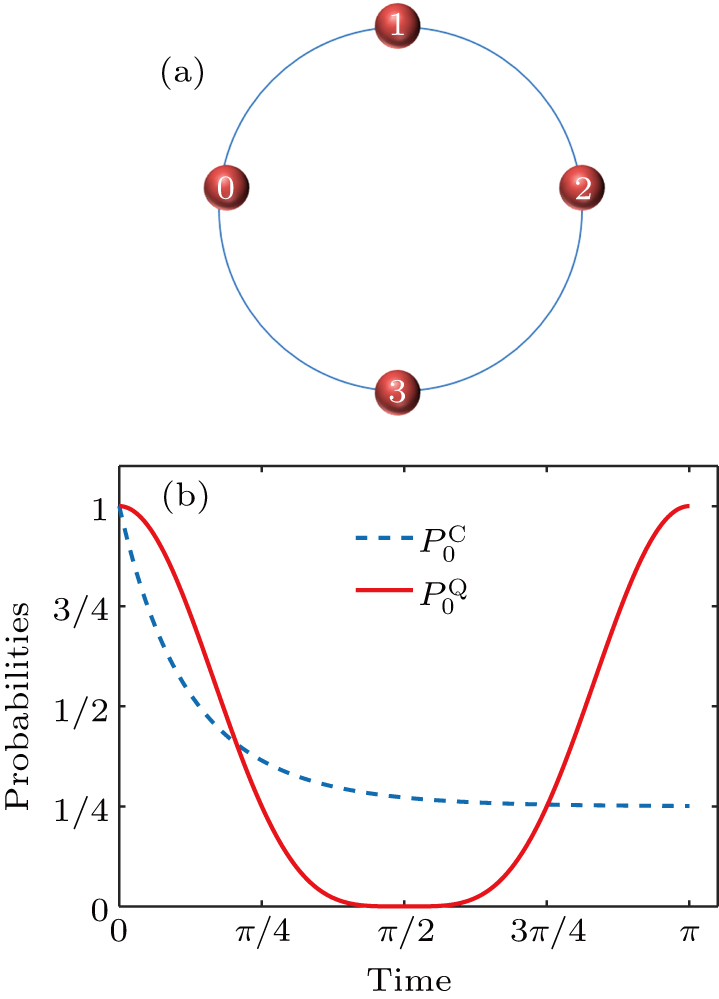
The concept of quantum CTRW was proposed in Ref. [23]. For the CTRW on an undirected circle, four nodes can be grouped in columns indexed by {0,1,2,3} as shown in Fig.
With such a generator matrix H, it is possible to construct a classical CTRW. The evolution of the probability distribution 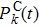
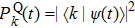
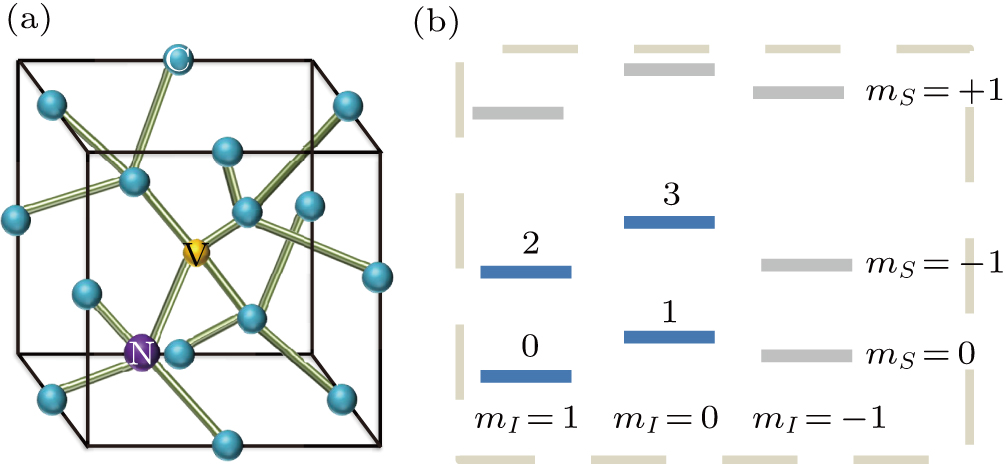
To implement quantum CTRW on a circle, an NV center in diamond was used in our experiment. The NV center is a defect in diamond as depicted in Fig.
Our diamond sample is a [100] facial bulk diamond and was mounted on a typical optically detected magnetic resonance confocal setup. The substitutional nitrogen concentration of sample is less than 5 ppb and the natural abundance of 13C is about 1.1%. By applying a 532-nm green laser and a 500-Gs (1 Gs = 10−4 T) static magnetic field aligned parallel to the symmetry axis of the NV center, the spin state of the NV center is effectively polarized to (mS, mI) = (0,+1).[24] The static magnetic field is created by a permanent magnet. A coplanar waveguide and a coil were used for feeding the microwave (MW) and radio frequency (RF) pulses, respectively.
| Table 1. The parameters of two-qubit programmable processor for quantum CTRW algorithm. . |
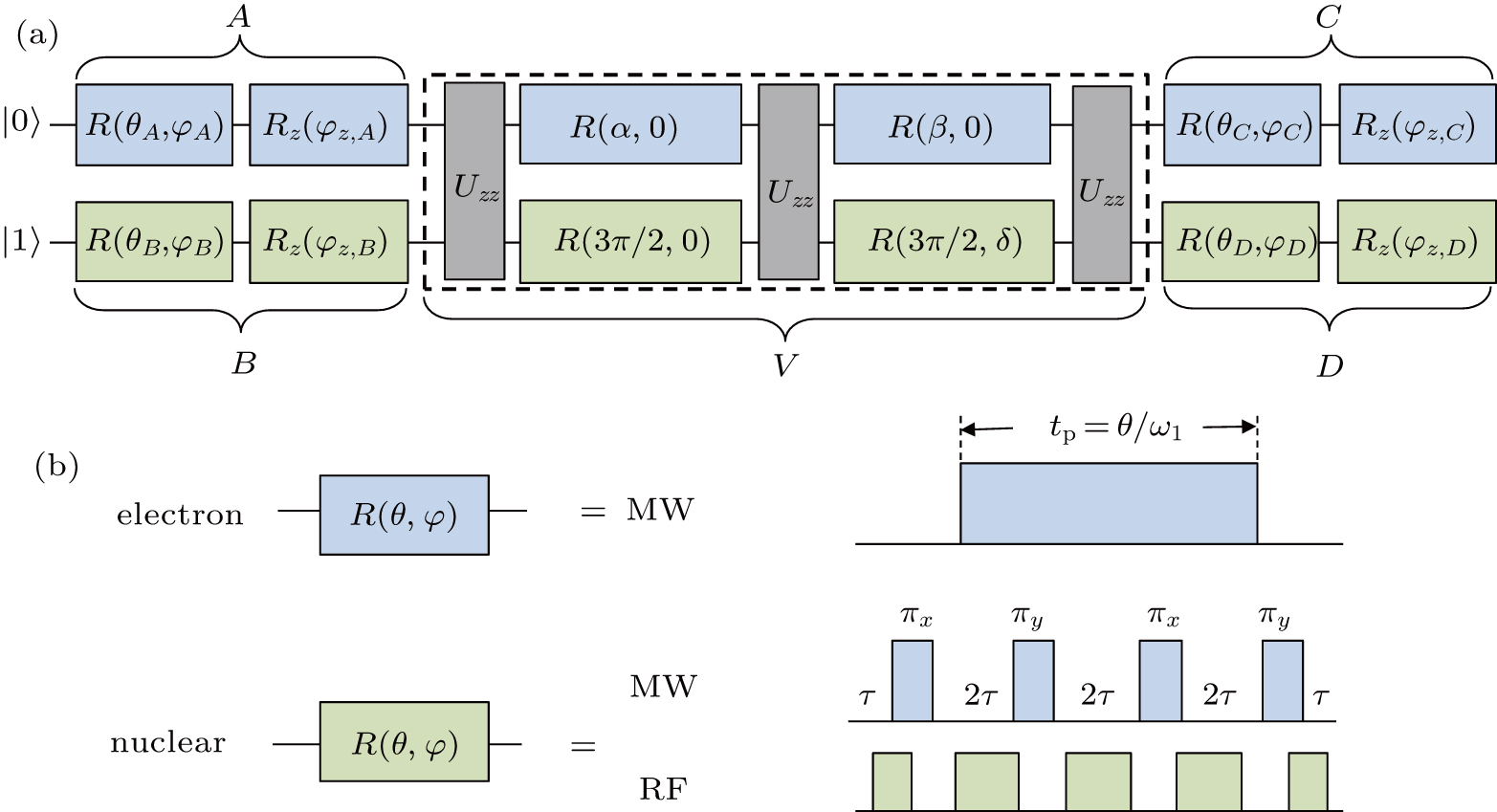
In our experiment, a two-qubit programmable quantum processor[25] was used to realize the time evolution of the quantum CTRW. The arbitrary two-qubit unitary operation can be implemented by the programmable quantum processor using the universal quantum circuit with altering the parameters. We chose the universal gate library consisting of single-qubit gates parameterized by the decomposition Rz(φz) · R(θ, φ) and an entangling two-qubit gate Uzz = exp(i π Sz ⊗ Iz). Here R(θ, φ) = exp[−i θ(cos φ Sx + sin φ Sy)] corresponds to a rotation of angle θ around the axis in the XY plane. Parameter φ denotes the angle between the axis of rotation and the X axis. Rz(φz) represents a rotation of angle φz around the Z axis. Sj (j = x, y, z) and Iz are the electron and nuclear spin operators, respectively. According to Eq. (
In the experiment, the single qubit rotations on the electron spin are implemented by a hard microwave pulse as shown in Fig.
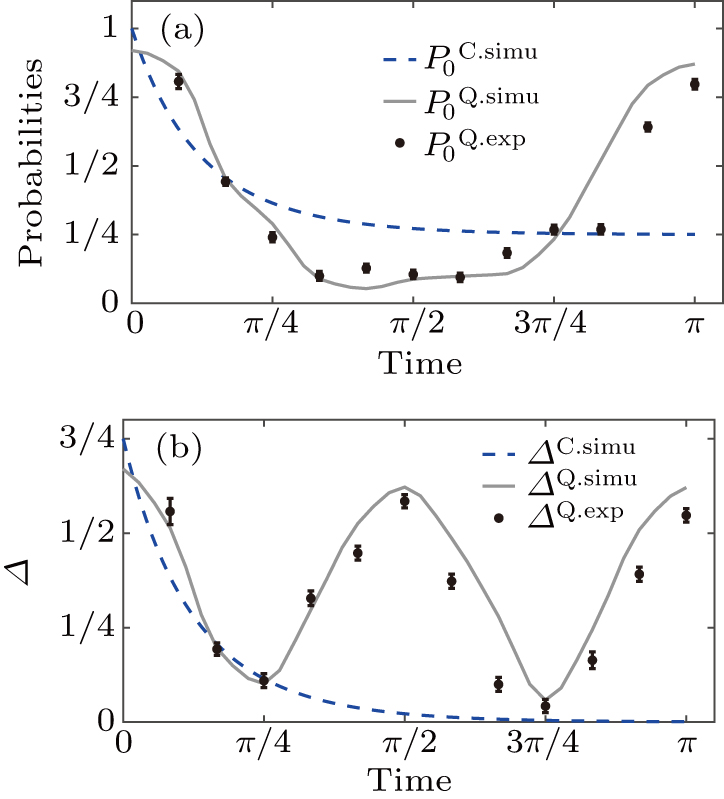
The probabilities as a function of time t are shown in Fig.
A straightforward method to characterize the uniformity of a distribution is to use the total variation distance between the given distribution and the uniform distribution. The classical and quantum total variation distance as a function of time t is
Figure
In conclusion, we have realized quantum CTRW algorithm with a solid-state programmable two-qubit quantum processor at room temperature. The programmable quantum processor which is based on the spin qubits in an NV center is used to implement the quantum CTRW algorithm by altering the parameters in the universal quantum circuit. The experimental results demonstrate that the quantum walk yields the oscillating behavior which is reversible and periodic, while the classical counterpart is essentially dissipative. Our work verifies the computational flexibility of the programmable processor, which paves the way to implement various algorithms in a large-scale room-temperature programmable quantum computation architecture.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] |