Project supported by the Yue-Qi Scholar of the China University of Mining and Technology (Grant No. 102504180004) and the 333 Project of Jiangsu Province, China (Grant No. BRA2018320).
Project supported by the Yue-Qi Scholar of the China University of Mining and Technology (Grant No. 102504180004) and the 333 Project of Jiangsu Province, China (Grant No. BRA2018320).
† Corresponding author. E-mail:
Project supported by the Yue-Qi Scholar of the China University of Mining and Technology (Grant No. 102504180004) and the 333 Project of Jiangsu Province, China (Grant No. BRA2018320).
To transform the exponential traveling wave solutions to bilinear differential equations, a sufficient and necessary condition is proposed. Motivated by the condition, we extend the results to the (2+1)-dimensional Kadomtsev–Petviashvili (KP) equation, the (3+1)-dimensional generalized Kadomtsev–Petviashvili (g-KP) equation, and the B-type Kadomtsev–Petviashvili (BKP) equation. Aa a result, we obtain some new resonant multiple wave solutions through the parameterization for wave numbers and frequencies via some linear combinations of exponential traveling waves. Finally, these new resonant type solutions can be displayed in graphs to illustrate the resonant behaviors of multiple wave solutions.
It is well known that the Hirota bilinear method is an efficient tool to construct exact solutions of nonlinear differential equations.[1,2] Based on Hirota bilinear forms, rational solutions, solitons solutions, rogue wave solutions, and periodic solutions could be obtained, e.g. in Refs. [3]–[7]. Meanwhile, the exact solutions play an essential role in proper understanding of qualitative features of the concerned phenomena and processes in various fields of science and engineering.[8–11] Recently, the lump solutions, lump type solutions and its various interaction solutions between lump solutions and other kinds of dispersive wave solutions are explored.[12–18] Meanwhile, using the Riemann–Hilbert method to construct N-soliton solutions has also attracted people's attention in the field of mathematical physics.[19,20] More recently, the linear superposition principle has been applied to exponential traveling waves of Hirota bilinear equations, and formed a specific sub-class of solutions from linear combinations of exponential wave solutions.[21,22] Some useful and extended results have been discussed in Refs. [23]–[27].
Let Υ be a polynomial in M variables, and then we consider a Hirota bilinear equation
 |
Substitute the linear combination function
For the above processes (
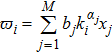
Moreover, Eq. (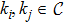

In what follows, we apply the linear superposition principle to extend the results for the (2+1)-dimensional KP equation, the (3+1)-dimensional g-KP equation and the BKP equation to obtain resonant multiple wave solutions in this paper.[29] To the best of our knowledge, they have not been obtained before.
In this section, we apply the linear superposition principle to solve the (2+1)-dimensional KP equation,[29] which is important because it serves as a kernel model in the universe Sato's theory,[30–32] that is,
Equation (
By Eq. (
Applying Theorem 1 and Eq. (
Solving Eq. (
Suppose that N1, N2 in N, N = N1 + N2. The N-wave variables 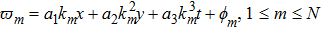
Taking θm = 0, we have
Taking θm = 2kπ + π/2, k ∈ K, then we have
In this section, we apply the linear superposition principle to solve the (3+1)-dimensional g-KP equation[29]
Equation (
Using Eq. (
Applying Theorem 1 and Eq. (
Solving Eq. (
Suppose that N1, N2 ∈ N, N = N1 + N2. We have the N-wave variables 
Using Theorem 2, any linear combination of exponential and trigonometric waves can be taken as follows:
Taking θm = 0, we have
Taking θm = 2kπ + π/2, k ∈ K, we have
Furthermore, we can obtain the following mixed-type function solutions like complexiton solutions
In this section, we apply the linear superposition principle to solve the (3+1)-dimensional BKP equation[29]
Equation (
Along with Eq. (
Applying Theorem 1 and Eq. (
Solving Eq. (
Suppose that N1, N2 ∈ N, N = N1 + N2. We have the N-wave variables 
Taking θm = 0, we have
Taking θm = 2kπ + π/2, k ∈ K, we have
Furthermore, we can obtain the following mixed-type function solutions like complexiton solutions
Suppose that N1, N2 ∈ N, N = N1 + N2. We have the N-wave variables 
Using Theorem 2, any linear combination of exponential and trigonometric waves reads
Taking θm = 0, we have
Taking θm = 2kπ + π/2, k ∈ K, we have
Furthermore, we can obtain the following mixed type function solutions like complexiton solutions
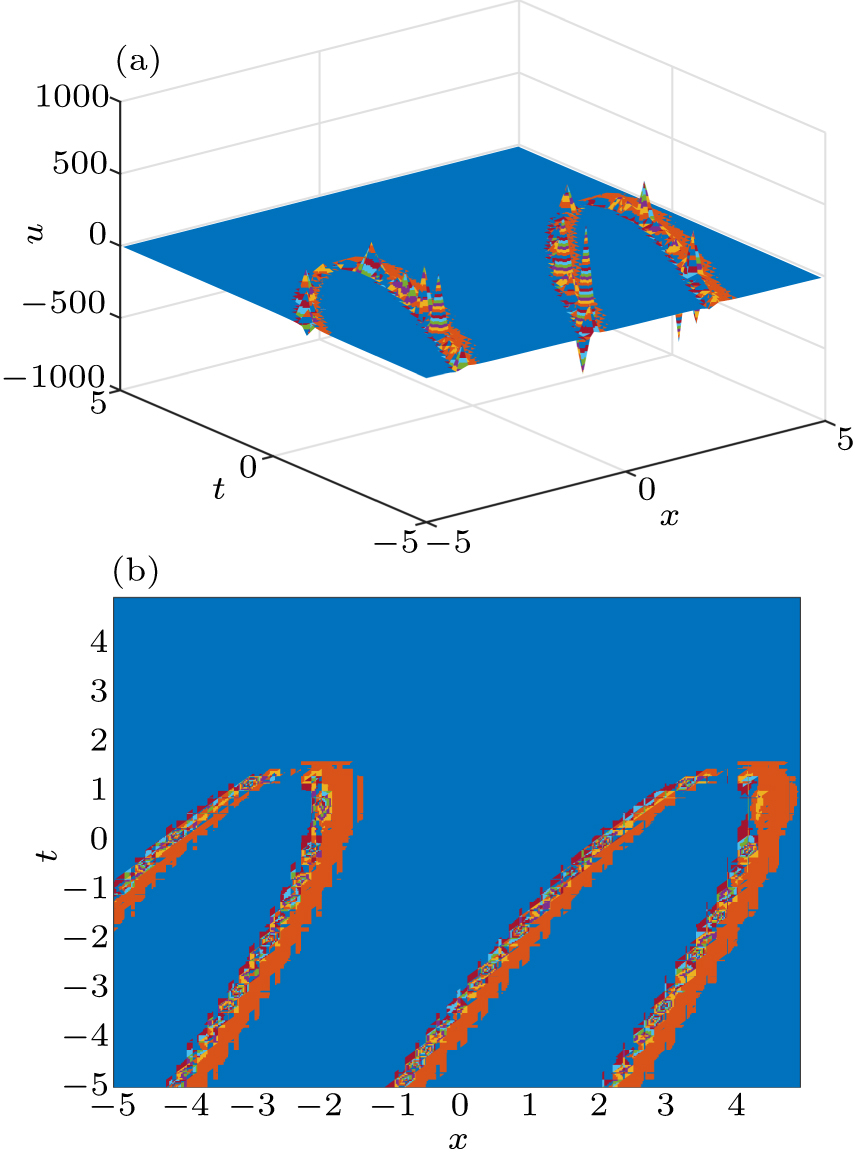
In order to better understand the resonant multiple wave solution, we display them by 3D-plot in Figs.
In summary, resonant multiple-wave solutions including soliton and complexion type solutions have been generated for a generalized (3+1)-dimensional KP equation with the aid of the linear superposition principle in complex field sense. These type solutions could help us better understand resonant nonlinear phenomena. Meanwhile, we would like to point that this paper can be regarded as an extension to the article.[29] Furthermore, for other types of special solutions of soliton equations appearing in this paper, we would further consider them in the future work.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] |