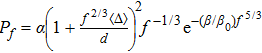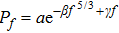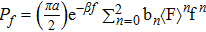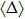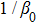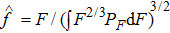† Corresponding author. E-mail:
Granular packings under gravity in frictional and frictionless silos were simulated and the influence of the wall friction on the normal force distribution was investigated. Although there is an obvious Janssen effect in frictional silos, only a slight influence on the geometry of packing was found. The law of normal force distribution is different for frictional and frictionless walls, which is related to the pressure profile. A modified formula with consideration of the pressure profile was well fitted to the simulation results.
Granular packing is very important for the mining industry and civil engineering. It is a suitable model to study about how the microscopic randomness and nonlinear contacts influence the macroscopic properties. Although the ideal conditions, such as periodic boundary or weightlessness, are appropriate to be achieved in simulations, the influence of gravity and boundary effect are very crucial and also difficult to be removed in experiments and engineering. In Dorbolo et al.ʼs experiment, the gravity was changed by a rotation tumbler and the results showed that Beverloo scaling law is still valid.[1] In the last few decades, the influence of sidewalls on granular systems has been studied and the results have shown that the wall friction plays a significant role in granular packing and flowing.[2–4]
A universal feature of the confined granular packing is that there is a saturation of vertical stress with depth, which was observed by Hagen[5] in 1852 and explained by Janssen[6] in 1895. The explanation contains two a priori assumptions: the ratio of vertical stress to horizontal stress is a constant and the friction on the wall is fully mobilized.[7,8] The general formula of the profile of vertical stress is 

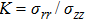
The normal force distribution is considered to be an important statistical characteristic in the granular system. In the last 20 years, the normal force distributions in granular packing and flows have been broadly investigated by both numerical simulations and experimental researches.[16–19] For a packing without external compression, Lovoll et al. found that the distribution function is consistent with a power law with an exponent 0.3 for small forces and an exponent decay with a constant 1.8 for larger forces.[20] In the static compressed system, there is a peak below the mean force with an exponential tail for forces larger than the mean force.[21] Meanwhile, van Eerd et al. simulated the packing of frictionless granules and fitted the parameters of the exponential tail in their force distribution. They suggested the tail as 

| Table 1.
Literature review of the formulas of force distribution. . |
Several formulas of the normal force distributions have been developed from empirical data or theoretical models (see Table
Although several fitting formulas exist, we wonder if they are still valid when the packing is confined and under gravity. In this paper, we simulated packings of 200000 spheres in a 3D cylinder silo. The effect of wall friction on the force distribution was investigated. It was found that the laws of force distribution vary with different wall frictions and the discrepancy is related with the Janssen effect.
The discrete element method (DEM)[37] has been widely accepted to be an effective method to solve problems of granular materials including static packings and flows.[38–41] DEM simulation includes calculation of contact forces among particles and solving the motion equation. Simulations of this work were performed on GPUs by the code developed with the DEM, in which interactions between two spheres were given by the Hertz–Mindlin model[42,43] and the integration of the motional equation was carried out using velocity-verlet scheme.[44]
According to the Hertz–Mindlin model, the normal and tangential forces between two contacting mono-sized spheres are
 |
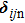
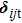
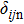
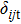
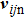
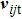


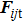
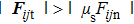
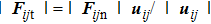

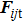
In a gravity field, the equations of motion for the spheres are
 |
In this work, 200000 spherical particles were randomly inserted into the space within the silo with a bottom diameter 0.012 m and the initial volume fraction was about 0.2. The spheres then fell freely and the packing process did not stop until the kinetic energy of the whole system was small enough. To accelerate the packing process, the drag force was added on each particle.[45] We then calculated the distribution of normalized normal force with various friction coefficients between particles and walls. The parameters of the spherical particles and the friction coefficients are listed in Tables
| Table 2.
Parameters of the particles in the simulation. . |
| Table 3.
Different friction coefficients used in the simulations. . |
To analyze the geometry of packing, Voronoi tessellation was used to measure the local volume fraction of each particle. The bond orientational orders Q4 and Q6 are calculated as[46]
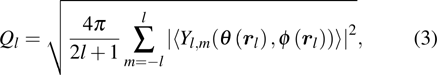 |
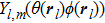
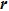

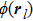
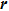
For the preparation, the particles were inserted randomly into the space inside the silo and no overlap between any two particles was guaranteed. Then, the gravity was activated to force the particles to fall to the bottom. Here, we followed Silbert et al.[45] to add a viscous damping which is helpful for accelerate the packing process. This process was finished when the total kinetic energy of the particles was less than 10−9 J.
For static granular packing under gravity, the results (Figs.
We also analyze the distributions of local bond orientational orders Q4 and Q6 in the packing.[46] No obvious crystallization is observed in the packing. From Fig.
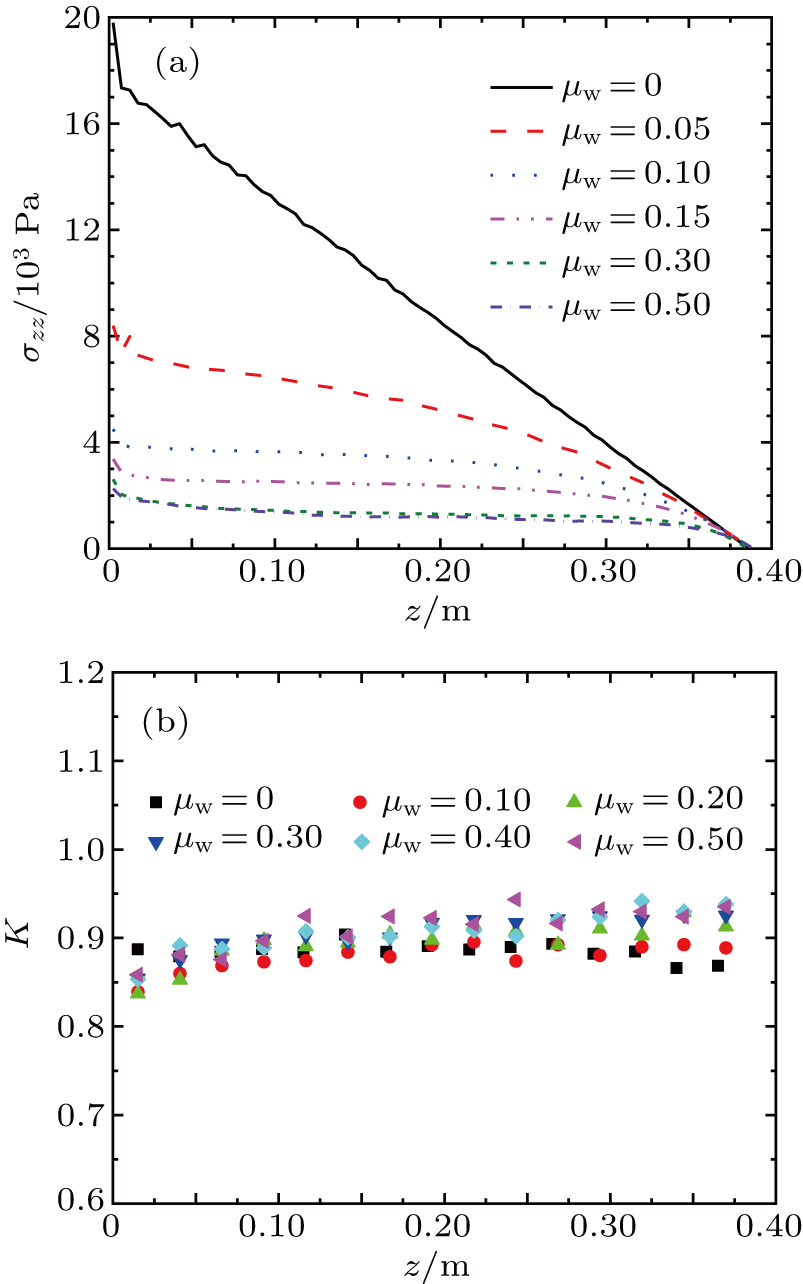
As introduced above, the packs of granular materials have a remarkable feature called the Janssen effect, which is the saturation of vertical stress at the bottom of the silo.[49,50] The appearance of the Janssen effect depends on the existence of the friction between grains and walls.[51] Figure 
In our simulations, the stress ratio K has slight fluctuations with different heights and is not influenced by μw (see Fig. 

We scanned wall friction coefficients μw from 0.0 to 0.5 and found that the distribution of normal forces is not invariant especially when the walls are frictionless enough (see Fig. 
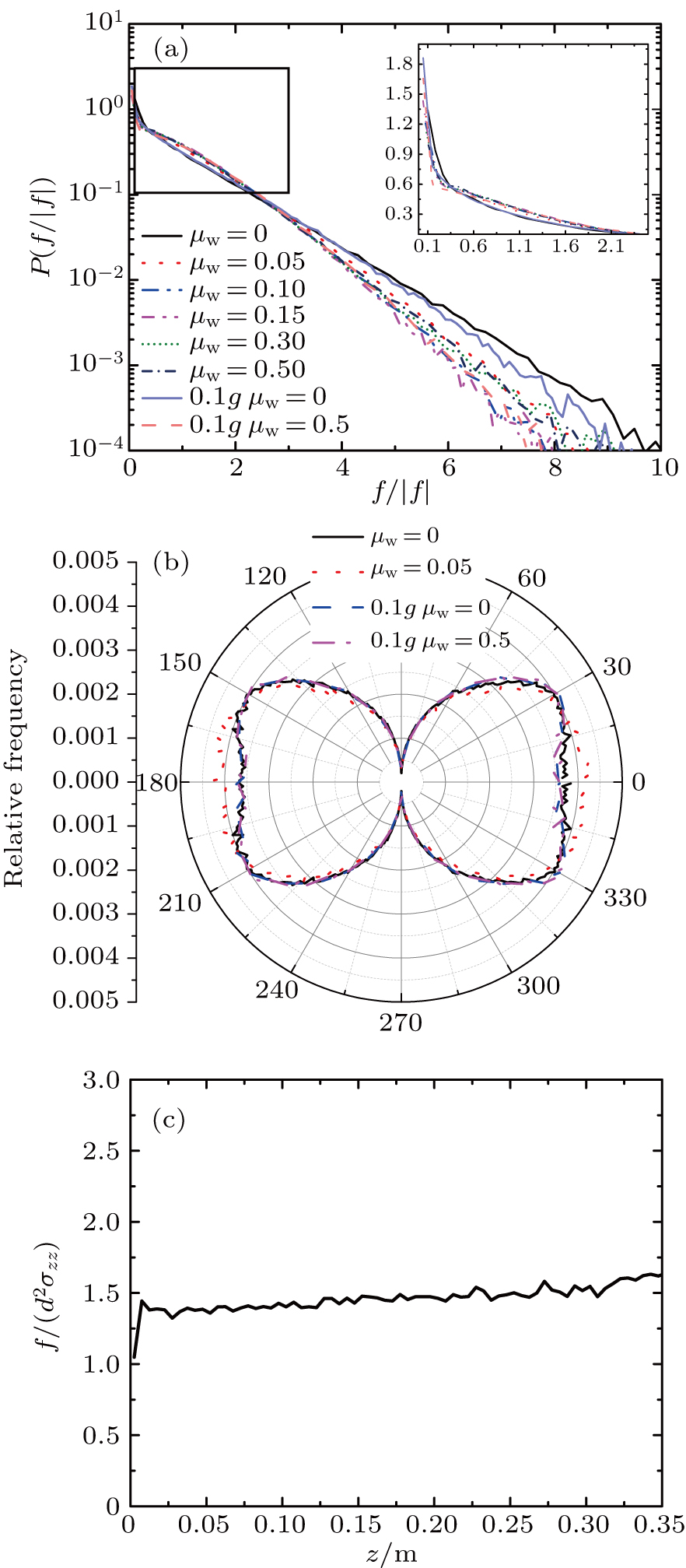 | Fig. 3. (a) Force distribution in simulation results with different wall frictions. 
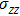
|
For the normal force distribution, there are several formulas developed from previous investigations. The q model, developed by Coppersmith et al., used the mean-field method to describe the force distribution in every layer (the whole space is vertically divided into layers and the thickness of the layers is equal to the diameter of the spheres) within the granular packing and considered the variances caused by gravity between the layers.[33] The formulas in most studies are more suitable to describe the granular packings when the influence of gravity is neglected. From Fig. 
 |
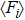
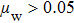
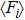
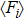
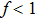
 | Fig. 4. (a) Simulation data is fitted with theories from Refs. [23], [24], [32], [34], and [36] In the simulations, the wall friction is set as 0.5. The enlarged graph shows the details of the fitting about normalized force from 0 to 2. (b) Simulation data is fitted with theories from Refs. [24], [34], and [36] along using Eq. ( |
In statistics mechanics, the velocity distribution of the ideal gas obeys the classical Maxwell–Boltzmann distribution; that is, 

This work studied the influence of wall frictions on the normal force distribution in granular packing with gravity. It was found that when the walls are frictionless, the distribution is different from that when the walls are not frictionless. This discrepancy can be explained using the Janssen effect; that is, the average normal force varies with the packing height when the walls are frictionless while it stays constant at most heights when the walls are frictional. We used the distribution function suggested in previous papers after considering the pressure profile and the fitted results support our explanations. However, more properties need to be studied in the future, such as the tangential force distribution in packings, the force distribution in granular flows, and the angular distribution of the contact force.
We thank Prof. Xiaohui Cheng for his instructive comments. We thank Dr. Liang-wen Chen for revising the manuscript and for the discussion.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] |