† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11704242) and the Natural Science Foundation of Shanghai, China (Grant No. 17ZR1447200).
The electrocaloric effect of the model ferroelectric BaTiO3 was investigated using phenomenological theory. The results indicate that the applied electric field strength is a key factor for the induced electrocaloric response and there are two distinguishing electrocaloric responses. When a moderate electric field is applied, the electrocaloric temperature variation is small but the electrocaloric strength is high. In contrast, the electrocaloric temperature variation is large but electrocaloric strength is low when a very high electric field is applied. These results are consistent with the experimental observations on BaTiO3 based bulk and thin film ferroelectric materials.
The electrocaloric (EC) effect refers to the isothermal entropy change ΔS or adiabatic temperature change ΔT of a dielectric material when an electric field is applied or removed. It has attracted great attention after the findings of 12-K temperature change in PbZr0.95Ti0.05O3[1] and more than 12-K temperature variation in P(VDF-TrFE) (55 mol%/45 mol%).[2] It has been particularly used for applications in cooling.[3–6] Lead-based electrocaloric materials show a large EC effect. However, the toxicity of lead has limited their applications. Therefore, lead-free ferroelectrics have been considered as better candidates for EC refrigeration, such as Bi0.5Na0.5TiO3-based ceramics,[7–9] and BaTiO3-based materials.[10]
The EC ΔT is closely related to the applied electric field. The electrocaloric strength ΔT/ΔE is also evaluated in the studies of EC effect. For instance, the large EC effects in PbZr0.95Ti0.05O3 were induced with a field of 77.6 MV/m,[1] which is huge in comparison with the dielectric strengths of common inorganic ferroelectric materials.
To gain an insight into the effect of the applied electric field, we conducted a theoretical study of the EC effect of the model ferroelectric BaTiO3 (BTO). A variety of experimental results has been reported on the EC effect of this material. In single crystal, the reported ΔT varies from 0.9 K@1.2 MV/m,[11] ∼1.2 K@1.2 MV/m,[12] to 1.6 K@1 MV/m.[13] In multilayer films, the ΔT varies from 1.8 K@17.6 MV/m,[14] to 7.1 K@80 MV/m.[15] These results indicate that the electric field strength is crucial for the EC response.
Based on the Maxwell equation, the EC adiabatic temperature change ΔT can be evaluated by the following equation[16,17]
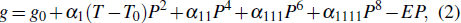 |
The EC ΔT of BTO at the different electric field strengths are plotted in Fig.
 | Fig. 1. (color online) Calculated EC ΔT of BTO at different electric field strengths by the phenomenological method. |
This profile of ΔT–T is consistent with the experimental observations.[11–13] Both the intensity and the width of the peak increase slightly with the increase of the applied electric field strength. The starting temperature of the ΔT peak is TC, and the stopping temperature is TCP. The predicted ΔT at 1 MV/m is 1.2 K, and the EC strength ΔT/ΔE is 1.2 × 10−6 K · m · V−1. These values agree with the experimental observations in the crystals of BTO as listed in Table
| Table 1. Data of EC properties of BTO and doped BTO in the literature. . |
In contrast, the EC ΔT–T profiles become broad and flat at the electric field strengths approaching and higher than ECP; as shown in Fig.
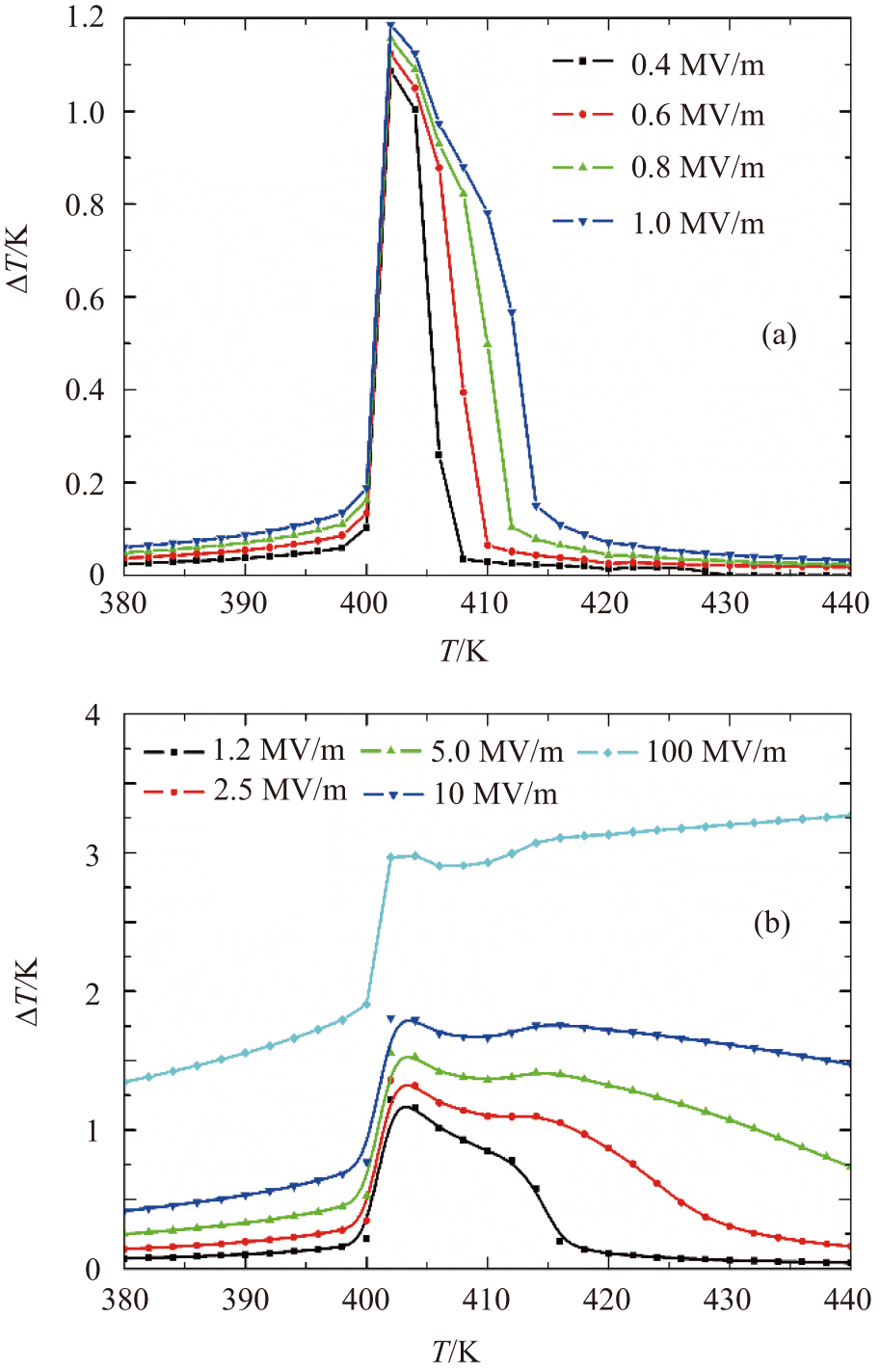
To disclose these two types of EC responses, we calculated
 | Fig. 2. (color online) The |
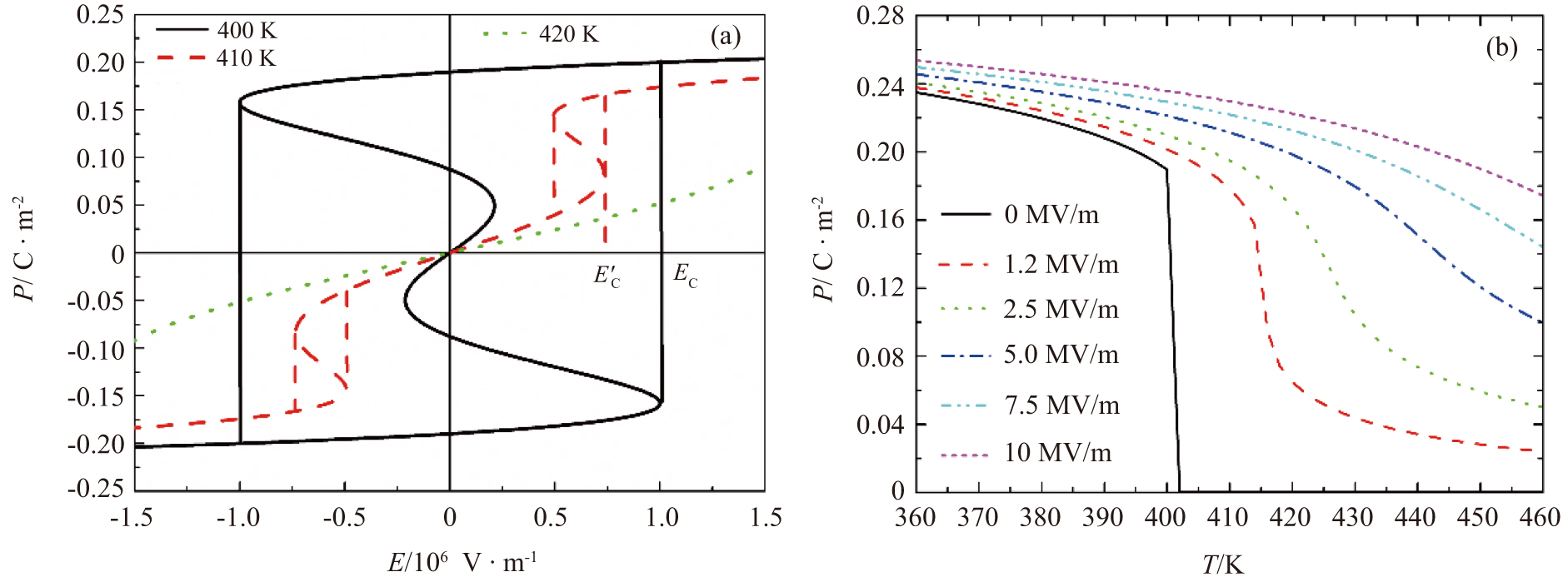
The electric field effect on the evolution of polarization is depicted in Fig.
Finally, we suggest that the finding in BTO is universal for ferroelectrics with first-order phase transition. At an electric field approaching ECP, ferroelectric materials have small ΔT about 1 K but high EC strength, and a sharp EC ΔT–T peak. Under a strong electric field, they produce giant ΔT but low EC strength, and a flat ΔT–T profile is observed. Since ferroelectric ceramics in bulk have low dielectric strengths around ECP, a sharp ΔT–T peak and tiny ΔT are normally observed. Because the dielectric strength is significantly enhanced in the thin films of ferroelectrics, a broad ΔT–T profile and large ΔT are observed. Table
In conclusion, the present study indicates that there are two distinguishing EC responses for ferroelectrics with first-order phase transition, which are mainly decided by the applied electric field. When the applied electric field strength is comparable with ECP, there exists a sharp ΔT–T peak with large ΔT/ΔE between [TC, TCP]. When the applied electric field strength is much higher than ECP, because of the vanishing of the first-order phase transition, the polarization is a weak function of temperature. The large EC ΔT can be induced by a large electric field but the EC ΔT/ΔE is quite small. A flat EC ΔT–T profile is observed commonly. This result explains the experimental observations on BTO-based materials from bulks to thin films. It also inspires researchers to find alternative ways to achieve both large EC ΔT and ΔT/ΔE simultaneously.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] |

