† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11704191), the Jiangsu Specially-Appointed Professor, the Natural Science Foundation of Jiangsu Province of China (Grant No. BK20171026), and the Six-Talent Peaks Project in Jiangsu Province, China (Grant No. XYDXX-038).
Most of the reported observations are about the dynamic properties of individual domain-walls in magnetic nanowires, but the properties of multiple stripe-domains have rarely been investigated. Here, we demonstrate a simple but efficient scenario for multiple domains injection in magnetic nanowires. The domain-chains (DCs), a cluster of multiple domains, can be dynamically generated with tunable static properties. It is found that the number of domains in a single DC can be dynamically adjusted by varying the frequency of microwave field (MF) and the period of spin-polarized current (SPC) intensity. The static properties of the DCs, i.e., its length, spacing, and period between neighboring DCs, can be dynamically controlled by regulating the frequency of MF and the intensity of SPC. We have also discussed the possibility of using domain-chains as information carries, which provides a meaningful approach for flexible multi-bit information storage applications.
With the development of nano-technology, high-density storage becomes an inevitable trend. Compared to the traditional hard disk, the racetrack memory based on magnetic domains (such as domain wall, skyrmion) can greatly improve the storage density. The dynamical behavior of magnetic domain walls[1–3] has been extensively investigated. As previously reported, due to the coupling effect of the antiferromagnetic layer film on the ferromagnetic layer, the magnetic domain wall width and the domain wall moving speed of the system change significantly.[4,5] In such domain wall-based racetrack memories, extensive research has been conducted on how to reduce the critical current density, reduce the influence of the pinning layer, and maintain the high-speed motion of the domain walls.[1,2,6] In particular, the spin-transfer torque (STT) driven motion of magnetic domain-walls and skyrmions has been demonstrated in magnetic nanowires.[7–16] The current-induced DW motion[12,17–20] has attracted much attention, since it provides an alternative candidate as information carries for the next-generation spintronic devices.[10,16,18,21–25] However, most of the research contents are about individual DW. From the application point of view, the multiple domain-based devices have the advances of manipulating flexibility and tunability in magnetic nanostructures.
In this work, we numerically investigated the dynamic nucleation of domain-chains (DCs) in magnetic nanowire using micromagnetic simulations. To distinguish them from isolate domains, we defined domain-chains as clusters comprised of multiple equally spaced domains, i.e., multiple domains forming one chain. The schematic diagram of a domain-chain containing two domains is shown in Fig.
Micromagnetic simulations have been done by using the public object-oriented micromagnetic framework (OOMMF) code at 0 K.[26] The OOMMF code has been extended to consider the Dzyaloshinskii–Moriya interaction (DMI)[27–29] and the SPC-induced magnetization dynamics by extending the Landau–Lifshitz–Gilbert (LLG) equation with additional DMI[27–29] and STT terms[7,30]
 |
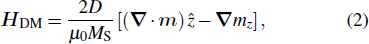 |
 |
The parameters used in the simulations are those of the Co/Pt bilayer with the presence of interfacial DMI.[31] The saturation magnetization Ms, exchange constant A, perpendicular magnetic anisotropy K, and DMI constant D are 5.8 × 105 A/m, 1.5 ×10−11 J/m, 0.7 MJ/m3, 3 mJ/m2, respectively. With the application of interfacial type DMI, the domain-walls appearing in the nanotrack will be the Néel type as confirmed from the simulated magnetization. The damping constant α, non-adiabatic STT parameter β, gyromagnetic ratio γ, and polarization rate of the SPC P are 0.3, 0.3, 2.211 × 105 m/As, and 0.4, respectively. The relative value of α and β is still in debate, and which will either boost or hinder the velocity of domain-walls in nanowires.[2,7,32,33] However, the nucleation scenario of domain-chains as proposed in this work will be hardly affected by this relative value. Without loss of generality, we choose the value of α = β = 0.3 (as used in Ref. [31]). The dimension of the nanotrack is 2400 nm × 60 nm × 1 nm along the x, y, and z directions, respectively. The used cells have a size of 2 nm × 2 nm × 1 nm, which is smaller than the characteristic length of material domains. There is no external magnetic fields were applied in all the simulations. For the parameters used in the simulation, u ≈ j·P·(4 ×10−11 m3/A·s), g = 2. The intensity of SPC is j ≈ 6.25 × 1013 A/m2 for u = 1000 m/s.
To create DCs successively, an external excitation microwave field was applied in the form of harmonic sinusoidal function Hy(t) = H0 sin(2πft) with f represents the excitation field. The microwave field with an amplitude of μ0 H0 = 5 T is applied locally to a Δx × Δy × Δz = 10 nm × 60 nm × 1 nm region near the left end of the nanotrack by injecting current pulses. The magnetization in the microwave “excitation” region can be reversed locally with the formation of domains.[16] The generated domains are driven by SPC to move rightward in the nanotrack. The scenario of nucleation of N-DCs as proposed in this work, are quite related to the frequency of the excitation magnetic field f, the amplitude of the excitation magnetic field H0, and the density of the driven spin-polarized current u. Depending on the requirement, suitable values of the three parameters can be chosen. Here, we use u = 1000 m/s corresponding to j = 6.25 × 1013 A/m2, however, the proposed scenario can also be realized using much lower current density with the loose of the DC velocity. As shown in Fig.
Figure
Figure
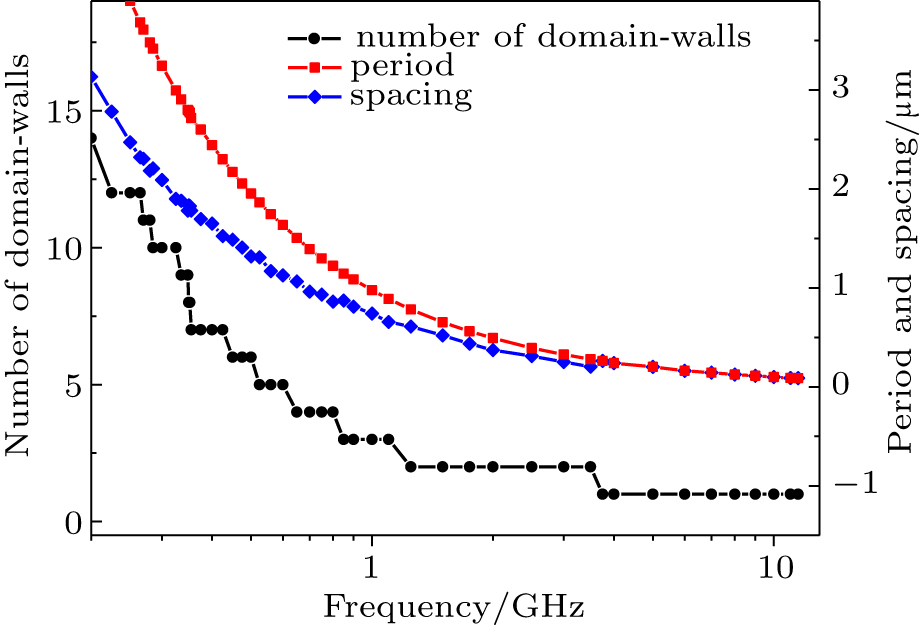
To understand how the frequency f of MF will affect the static properties of the DCs, we studied the temporal magnetization variation in the nanotrack with reducing f from 8 GHz to 0.5 GHz. As shown in Fig.
 | Fig. 3. (color online) Snapshot of the out-of-plane magnetization mz for N-domain-chain under various microwave field frequency f, where N is the number of individual domains in each domain-chain. |
Figure
So far, we have demonstrated the possibility of controlling DCs’ properties by varying the microwave field frequency. However, the manipulation of DCs by controlling the excitation MF frequencies is not efficient from the application point of view with the requirement of excitation antenna preparation. Alternatively, with a fixed excitation MF frequency f, DCs of various properties can also be generated by temporally changing the intensity u of SPC. Figure
We have numerically studied the dynamical creation of magnetic domain-chains, comprised of multi-single-domains, in magnetic nanowires. It has been demonstrated that both the frequency f of the excitation MFs and the temporal format of the SPC intensity can obviously affect the typical characteristics of generated domain-chains: the number N of individual domains in each DC, the period of DCs, and the distance between adjacent DCs. Our demonstrated scheme of multiple DCs nucleation could enrich the fields of using magnetic domains for the design of racetrack memory and logic devices.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] |