† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11704191), the Jiangsu Specially-Appointed Professor, the Natural Science Foundation of Jiangsu Province of China (Grant No. BK20171026), and the Six-Talent Peaks Project in Jiangsu Province, China (Grant No. XYDXX-038).
In this work, we experimentally investigated the thermal stability of the interlayer exchange coupling field (Hex) and strength (–Jiec) in synthetic antiferromagnetic (SAF) structure of [Pt(0.6)/Co(0.6)]2/Ru(tRu)/[Co(0.6)/Pt(0.6)]4 multilayers with perpendicular anisotropy. Depending on the thickness of the spacing ruthenium (Ru) layer, the observed interlayer exchange coupling can be either ferromagnetic or antiferromagnetic. The Hex were studied by measuring the magnetization hysteresis loops in the temperature range from 100 K to 700 K as well as the theoretical calculation of the –Jiec. It is found that the interlayer coupling in the multilayers is very sensitive to the thickness of Ru and temperature. The Hex exhibits either a linear or a non-linear dependence on the temperature for different thickness of Ru. Furthermore, our SAF multilayers show a high thermal stability even up to 600 K (Hex = 3.19 KOe, –Jiec = 1.97 erg/cm2 for tRu = 0.6 nm, the unit 1 Oe = 79.5775 A·m–1), which was higher than the previous studies.
Spin-transfer-torque magnetic random access memories (STT-MRAMs) is one of the most attractive candidate to satisfy the need of memory markets owing to their outstanding performance, such as non-volatile, low power consumption, unlimited endurance, wide operating temperature, and long-term data retention.[1–8] However, how to realize the high density of current MRAM is the main bottleneck limiting their practical applications, which is due to the stray magnetic fields generated by magnetic layers. Recently, perpendicularly magnetized tunnel junctions (p-MTJs) that including synthetic antiferromagnetic (SAF) layers have been used to promote the development of STT-MRAMs. The introduction of SAF layers into MRAM devices suppresses the effect from the stray magnetic field, extends the operation temperature range, and improves the thermal stability.[9–11]
The SAF structure is mainly composed of two ferromagnetic (FM) layers separated by a nonmagnetic spacing layer (e.g., Ru, Rh, or Ir),[12–14] where the two FM layers are antiferromagnetically or ferromagnetically coupled by varying the thickness of the spacing layer. Thanks to their perceived advantages of strong magnetic stability, high thermal stability, and sensitive magnetic moment rotation, SAF structure with perpendicular magnetic anisotropy (PMA) has been extensively studied.[15,16] For instance, the spin-orbit torque induced switching of the two magnetic layers in Co/Ru/[Co/Pt]2[17] and completely compensated Pt/[Co/Pd]/Ru/[Co/Pd][18] SAF structures. The antiferromagnetic interlayer exchange coupling (IEC) and the outstanding performance in a wider temperature range are the key fundamental characteristics of SAF multilayers, which are important for such large-scale industrial application as field sensors, magnetic recording, and magnetic random-access memory.[19,20] As required by the potential military and aerospace applications, it is highly desirable to control the IEC of multilayers by changing external physical parameter, such as temperature. However, the widespread Pt/Co-based SAF multilayer with an Ru spacer is still a challenge due to the structural discontinuity or intermixing that occurs at high temperature. In this work, we experimentally investigated the temperature-dependent IEC properties of SAF multilayers comprised of two Pt/Co ferromagnetic layers and an Ru spacing layer. It is showing that the interlayer exchange coupling field (Hex) and coupling strength (–Jiec) are highly dependent on the Ru spacer thickness (from 0 nm to 1.6 nm) and the measuring temperature (from 100 K to 700 K).
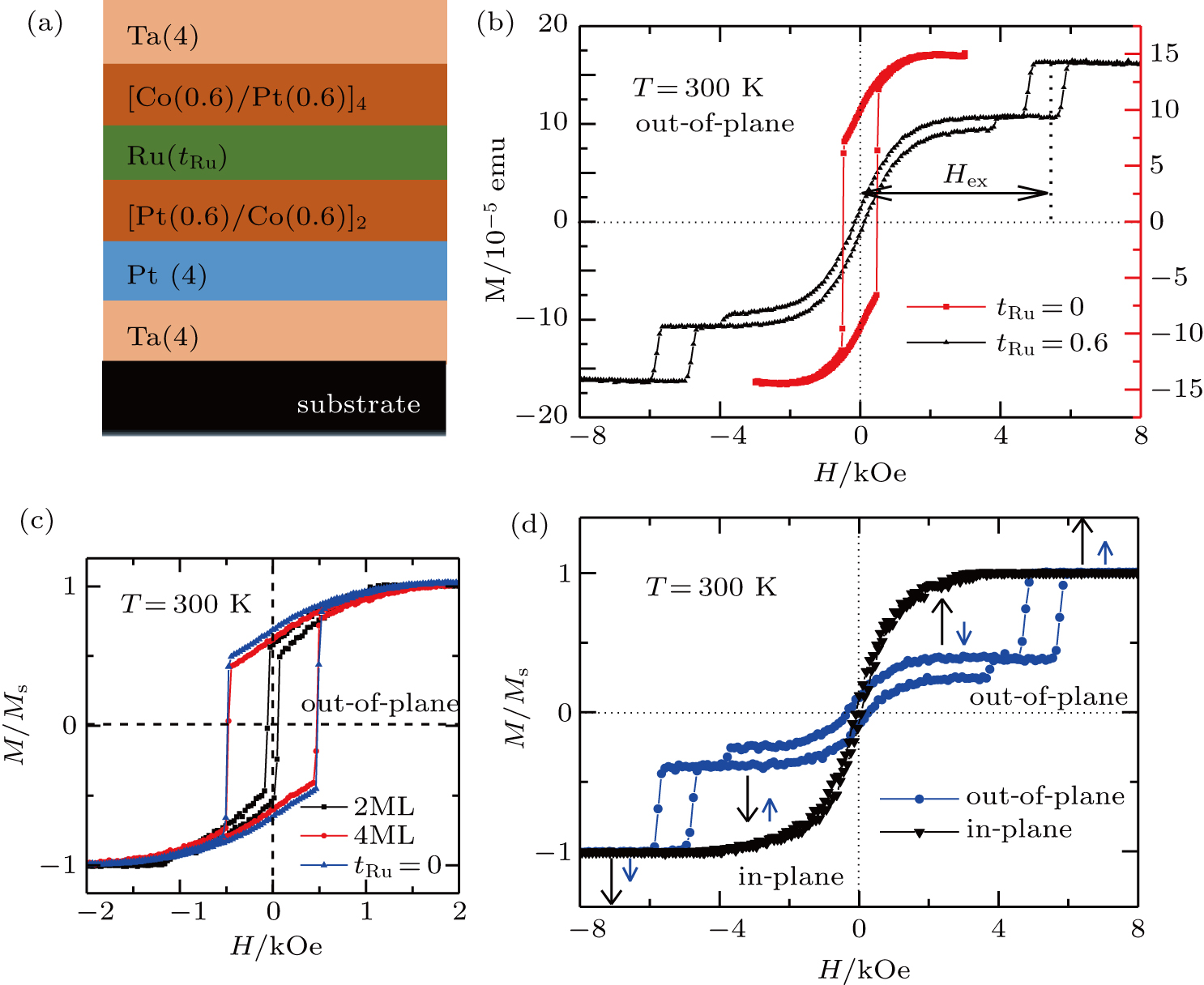
Ta(4)/Pt(4)/[Pt(0.6)/Co(0.6)]2/Ru(tRu)/[Co(0.6)/Pt(0.6)]4/Ta(4) thin film stacks were deposited on a thermally oxidized silicon wafer use DC magnetron sputtering techniques at room temperature (RT). Argon gas (∼ 2.3 mTorr, 1 Torr = 1.33322×102Pa) was used during the sputtering process with a background pressure of 2 × 10–9 Torr, and the deposition rates for Ta, Pt, Co, and Ru were 0.026, 0.544, 0.14, 0.21, and 0.10 Å/s, respectively. Numbers in parentheses are the nominal thicknesses in unit nm. In the thin film stacks, the bottom ferromagnetic stack ([Pt(0.6)/Co(0.6)]2) and the top ferromagnetic stack ([Co(0.6)/Pt(0.6)]4) are antiferromagnetically or ferromagnetically coupled through the spacing layer depending on the Ru thickness. We prepared five SAF multilayers with the thickness of Ru, tRu = 0, 0.6, 0.9, 1.2, 1.6 nm, respectively. To compare the effect of the thickness of FM layer [Pt(0.6)/Co(0.6)]x, we also prepared two reference samples Ta(4)/Pt(4)/[Pt(0.6)/Co(0.6)]x/Ta(4) (x = 2 and 4, respectively). For simplicity, these two reference samples will be named as 2ML and 4ML. Vibrating sample magnetometer (VSM) was used to measure the in-plane and out-of-plane magnetization hysteresis loops of the sputtered magnetic thin film stacks. A series of hysteresis curves were achieved by varying the magnetic field at center sweeping rate using electro-magnet at different temperatures. The measurements done below RT were accomplished by a continuous flow of gas through liquid nitrogen cooled, and the measurements done above RT were carried out with the sample chamber heated electrically.
Figure
In order to study the relationship between the exchange coupling field (Hex) and the thickness of Ru spacer, we measured the out-of-plane M–H loops of four samples with different thickness of Ru at room temperature. Figure
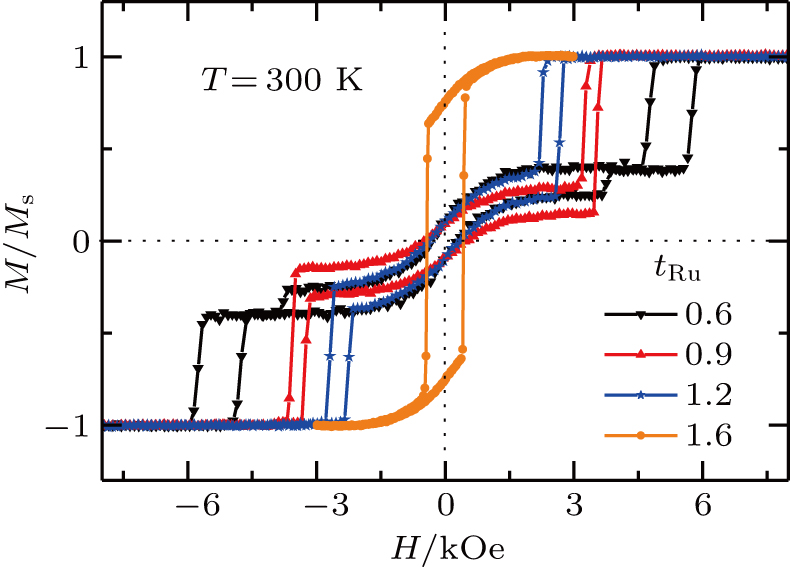 | Fig. 2. (color online) The dependence of the normalized out-of-plane M–H loop on the thickness of the Ru spacing layer in the p-SAF structure at 300 K, for tRu = 0.6, 0.9, 1.2, 1.6 nm. |
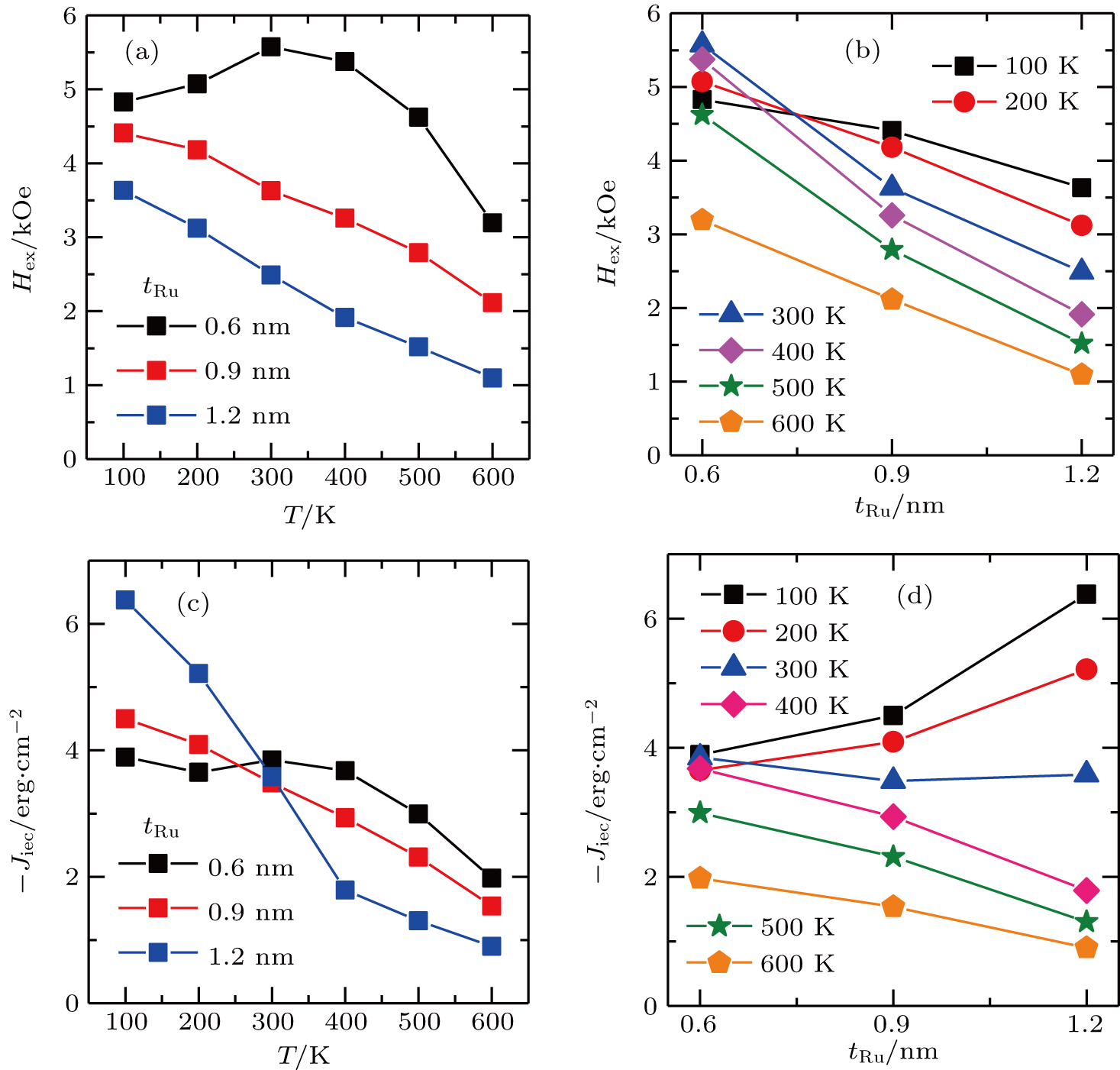
From the application point of view, the thermal stability of the interlayer exchange coupling field (Hex) and strength (–Jiec) is the meaningful factor for the development of novel spintronic devices based on SAF multilayers. It has been found that the Hex and –Jiec of SAF multilayers varies significantly with temperature owing to the Fermi surface state of the spacing layer, which has been studied in previous reports.[26,27] Figure
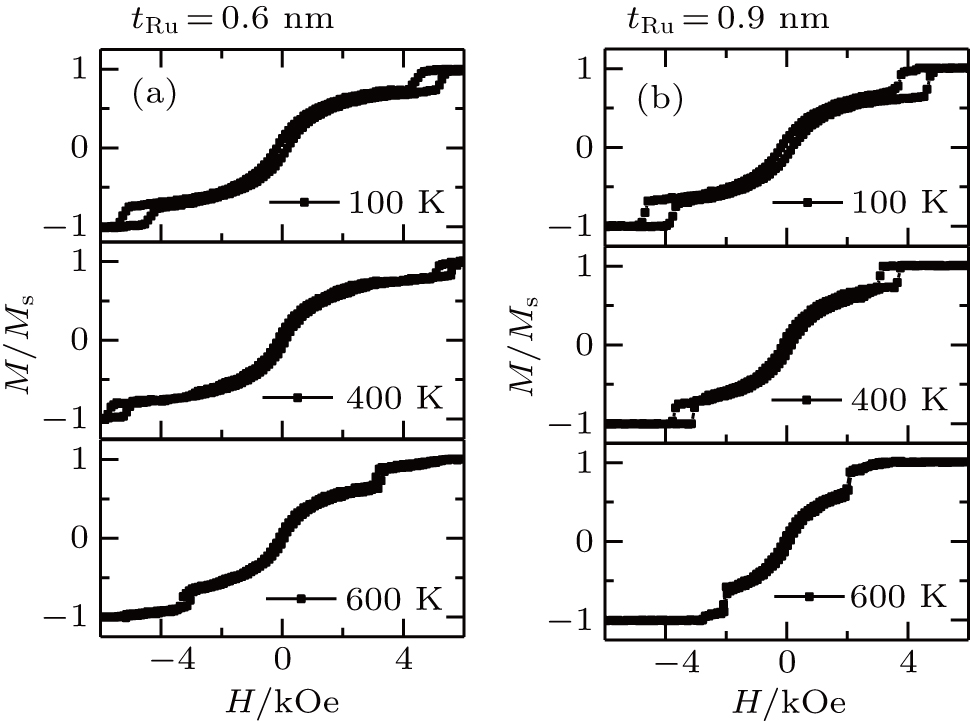 | Fig. 3. Temperature dependence of the normalized out-of-plane M–H loops of SAF multilayer structures with (a) tRu = 0.6 nm and (b) tRu = 0.9 nm. |
The temperature dependence of Hex for SAF multilayers with three different Ru thicknesses are shown in Fig.
The temperature dependence of –Jiec for SAF multilayers with three different Ru thicknesses are shown in Fig.
In this work, the temperature dependence of the interlayer exchange coupling field (Hex) and coupling strength (–Jiec) in magnetron sputtered SAF multilayers with perpendicular magnetic anisotropy have been studied experimentally and theoretically. It is experimentally demonstrated that the IEC behavior of [Pt(0.6)/Co(0.6)]2/Ru(tRu)/[Co(0.6)/Pt(0.6)]4 multilayers is very sensitive to the spacing layer Ru and the temperature variation. It is worth pointing out that our SAF multilayers possess a much higher thermal stability even at the temperature of 600 K (Hex = 3.19 KOe, –Jiec = 1.97 erg/cm2 for tRu = 0.6 nm) in comparison with other reported values. The enhanced Hex and Jiec make [Pt/Co] multilayer structure possess large perpendicular magnetic anisotropy (PMA) energy, which enable us to obtain an enlarged AF-coupled working field range, i.e., a wider field range hosting AF-skyrmions. On the other hands, the large anisotropy for the development of high storage density device is valuable. Our results would provide benefit information for novel spintronic applications requiring SAF multilayers of better magnetic performance and thermal stability.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |