† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11774239), the National Key Research and Development Program of China (Grant No. 2016YFB0700700), the Fund from Shenzhen Science and Technology Innovation Commission (Grant Nos. JCYJ20170412110137562, JCYJ20170818093035338, and ZDSYS201707271554071), the Natural Science Foundation of Shenzhen University (Grant No. 827-000242), the High-End Researcher Startup Funds of Shenzhen University (Grant No. 848-0000040251), and the Supporting Funds from Guangdong Province for 1000 Talents Plan (Grant No. 85639-000005).
The family of ABX half-Heusler materials, also called filled-tetrahedral structures, is a special class of ternary compounds hosting a variety of material functionalities including thermoelectricity, topological insulation, magnetism, transparent conductivity and superconductivity. This class of compounds can be derived from two substitution approaches, i.e., from Heusler materials by removing a portion of atoms forming ordered vacancies thus becoming half-Heusler, or from tetrahedral zinc blende compounds by adding atoms on the interstitial sites thus become filled-tetrahedral structures. In this paper, we briefly review the substitution approaches for material design along with their application in the design of half-Heusler compounds; then we will review the high-throughput search of new half-Heusler filled-tetrahedral structures and the study of their physical properties and functionalities.
Along with the fast development of computation resources and methods, materials design has become a substantial method for searching physically interesting and technologically critical functional materials. Diamond-like semiconducting compounds such as Si and GaAs (a synthetic material designed in laboratory[1]) formed by two sets of face-centered cubic (fcc) sub-lattices are one of the most significant classes of materials for industry, which are essential for information, electrical, energy, healthcare and aerospace technologies.[2–8] This class of materials has been the focus of materials design[9–11] due to the quest of new technologically useful semiconductors. The group of Heusler compounds formed by four sets of fcc sub-lattices shows broad variety of physical properties, including half-metallicity,[12] Kondo effect,[13] superconductivity,[14] topological insulation,[15] and magnetic topological Weyl fermion.[16] The family of half-Heusler compounds with three sets of face-centered sub-lattices are closely related to both diamond-like and Heusler materials. As illustrated in Fig.
The substitution approach of materials design that derives a new materials family from a previously known parent materials family by partially substituting the elements in the chemical formula is an efficient rational approach for designing new compounds. The physical properties of the new materials are closely related to their parent materials systems, as the local structural motifs are to some extent maintained during the substitution process. Numerous physically interesting and technologically critical functional materials (e.g., in Refs. [2], [4], [9]–[11]) have been designed via different types of substitution approaches.
The most straightforward substitution is to substitute part of the elements by the elements from the same group in the periodic table (i.e., iso-group substitution), which could be applied to the wide-gap semiconductor cubic SiC[43] that can be derived from Si by substituting half of the Si atoms by C, specifically replacing all the Si atoms on one of the two fcc sub-lattices in the diamond structure. However, applying the iso-group substitution to other materials systems such as III–V and II–VI semiconductor alloys, in which one of fcc sub-lattices in the diamond-like structure is occupied by two types of elements, results in thermodynamically metastable phases[44–53] due to the strain energy arising from size-mismatch between the constituents. Note that the same atomic substitution in cubic SiC does not apply to the Si–Ge system since, chemically, Si and C are rather different thus gaining large chemical energy, whereas Si and Ge are quite similar. Therefore, the number of thermodynamically stable compounds derived from iso-group substitution is rather limited. In contrast, simultaneous substitution using multiple types of elements from different groups in the periodic table has been successfully applied for predicting new stable compounds in their simplest form with two types of substituting elements[9] called co-substitution.
In the co-substitution approach,[9] a new compound is derived from the parent compound by replacing one type of elements by pairs of elements from other groups in the Periodic Table while keeping the number of valence electrons per atom unchanged (e.g., replacing Zn by Cu and In). The mechanism for stabilizing a compound in co-substitution is analogous to the co-doping[54–56] physics involving pairs of donor and acceptor defects. The electrons transferring from donor to acceptor levels, and the donor-acceptor electrostatic attraction along with the atomic relaxations upon donor–acceptor pairing, are the main factors that stabilize the co-doping system. Co-substitution can be viewed as a 100% co-doping. In addition to the above energy saving factors, the ordering energy gained by forming ordered pattern in 100% co-doping that reduces strain energy, further stabilizes the co-substitution system. Co-substitution has been widely used in experimental and theoretical studies, leading to the discovery of many new stable compounds.[11,57–63] Several mutated types of co-substitutions were also used in materials design, e.g., co-substitution with ordered vacancies[10,18,64–67] and co-substitution with filled interstitials.[17,19,68–74]
The substitution along with the formation of ordered vacancies in diamond-like structures was discussed in 1960 as a super-cell structure of semiconductors[10] with
According to Eq. (
There are plenty of crystal structures in nature that can be derived from other structures by filling some of their interstitial sites.[68–74] Filling the interstitial sites in semiconductors usually leads to metallic phases, as the interstitial defects are usually donors. If combining acceptor-like substitutions (e.g., Sn on Sb) with filled interstitials to compensate the variation of valence electrons, one can design semiconductors stabilized by electron count even in complicated structures, such as the LaCo4Sb9Sn3 filled Skutterudite semiconductor derived from the CoSb3 Skutterudite semiconductor by filling La with three valence electrons on the interstitial site and substituting three Sb by three Sn atoms losing three valence electrons.[69]
The co-substitution approach along with filled interstitials has been extensively applied to diamond-like structures, leading to the discovery of many semiconducting compounds.[71–74] The diamond structure is one of most loosely packed three-dimensionally bonded structures in nature. In the unit cell of diamond structure, there are four fcc sub-lattices (see Fig.
The half-Heusler compounds (e.g., LiZnSb) can be derived from the Heusler-like A3X-type compounds (e.g., Li3Sb) by co-substitution with ordered vacancies (e.g., substituting one Li by Zn and removing another Li), which can also be viewed as filled interstitial structures derived from zinc blende compounds as discussed above. In the next section, we will discuss the focusing study of new half-Heusler compounds.
New half-Heusler ABX compounds can be derived from the existing Heusler materials or zinc blende compounds by introducing ordered defects (vacancies or interstitials), as discussed above; they can also be derived from the previously known half-Heuslers simply via iso-formula species replacement (e.g., from LiZnN to NaZnN). However, one needs to check (i) whether the derived nominal compounds have the cubic half-Heusler structure, i.e., structural determination; and (ii) whether they are thermodynamically stable against disproportionation into competing phases, i.e., thermodynamic stability analysis, which are the main questions we are facing when predicting new multinary materials. Once the new compounds are predicted, theoretical evaluations of their physical properties and functionalities could be performed to suggest candidate multifunctional materials. Figure
 | Fig. 2. (color online) Schematic diagram for the high throughput prediction of functional materials. |
Prediction of the lowest-energy structure of a multinary compound can be solved successfully based on, e.g., the global space group optimization (GSGO) method[75] that starts from randomly selected lattice vectors and random atomic positions within a cell as input for a sequence of ab initio calculations of total energy of locally relaxed trial structures to search for a global minimum via an genetic-algorithm selection. The GSGO method is successfully applied in predicting the lowest-energy structures of ABX compounds (e.g., NaBaAs[76]). Analogous methods including simulated annealing,[77] evolutionary algorithm,[78,79] random search,[80] and particle-swarm optimization,[81] are also successful for a number of focused cases of structure prediction.[78–81] However, these coordination-based optimization methods[75,78–81] typically require significant computational resources to solve the lowest-energy structure of a single compound and is not tractable for high-throughput predictions of new materials.
Alternatively, one can use prior knowledge of the crystal structures of the existing compounds by constructing a tensor T(ci, ej)[82,83] for the known structures of given compositions (ci) and sets of elemental constituents (ej). T(ci, ej) = “null” if for the composition ci, e.g., ABX, and the set of elemental constituents ej, e.g., NaZnN, the compound has not been reported yet. One can then construct a probability density P(T(ci, ej)) based on the tensor T(ci, ej), considering (i) compounds in the same composition ci (e.g., NaZnN derived from LiZnN, NaZnP, NaZnAs, or NaZnSb, each derivation suggesting a structure), and (ii) compounds that the composition ci can be derived from using e.g., the substitution approaches discussed in Section
The next step after structural determination for predicting the new compound is the evaluation of its stability relative to its competing phases by comparing their total energies or formation enthalpies. However, the standard approximations to density functional theory (DFT),[85,86] namely, the local density approximation (LDA)[87,88] or the generalized gradient approximation (GGA)[89] have to some extent numeric errors for predicting compounds’ formation enthalpies, especially when the compounds and their competing phases belong to different chemical classes (e.g., metal or non-metal). In Ref. [90], a computationally inexpensive theoretical approach based on GGA+U calculations with fitted elemental-phase reference energies (FEREs) that can be used for accurate predictions of the ΔHf values of binary and multinary solid compounds involving chemical bonding between metals and nonmetals (such as pnictides, chalcogenides, halides). A set of FERE values[90] were obtained using an extensive set of 252 binary compounds with measured heat of formations, showing that the 252 formation enthalpies can be reproduced with the mean absolute error of 0.054 eV/atom after fitting instead of 0.250 eV/atom before fitting (see Fig.
 | Fig. 3. (color online) Histogram showing absolute errors of the GGA (upper part) and of the FERE approach (lower part) in reproducing measured enthalpies of formation for 45 binary pnictides and chalcogenides containing 3d transition metals. Dashed lines represent the mean absolute error of the two methods corresponding to the full set of 252 binary compounds (Figure adapted from Ref. [90]). |
In Refs. [76] and [84] on the prediction of new ABX half-Heusler compounds, the thermodynamic stability analysis is performed in the elemental chemical potentials space using the information of compounds’ formation enthalpies (ΔHf). A new compound (e.g., ABX) is considered stable under the thermodynamic equilibrium conditions if there are values of the elemental chemical potentials (e.g., ΔμI, I = A, B, X) that do not favor the formation of elemental (thus ΔμI < 0, I = A, B, X), binary (e.g., AlBm thus lΔμA + m Δ μB < ΔHf(AlBm)), ternary (e.g., AlBmXn thus lΔμA + mΔμB + nΔμX < ΔHf(AlBmXn)) competing phases, but favor the formation of the target compound under thermodynamic equilibrium condition (e.g., for ABX, ΔμA + ΔμB + ΔμX = ΔHf(ABX)). The area in the elemental chemical potentials space that includes all the ΔμI values favoring the target compound but not competing phases can then be identified as the stability region. Figure
 | Fig. 4. (color online) The allowed chemical potential regions (yellow) in the chemical potential space of three cubic semiconducting ABX compounds, indicating also some of the phases competing with the stability of the ABX structure (Figure adapted from Ref. [91]). |
Following the above two steps of materials prediction (structure determination and thermodynamic stability analysis), 235 new ABX compounds with eight valence electrons (e.g., LiMgSb)[76] and 54 new ABX with 18 valence electrons (e.g., TaIrGe, see Fig.
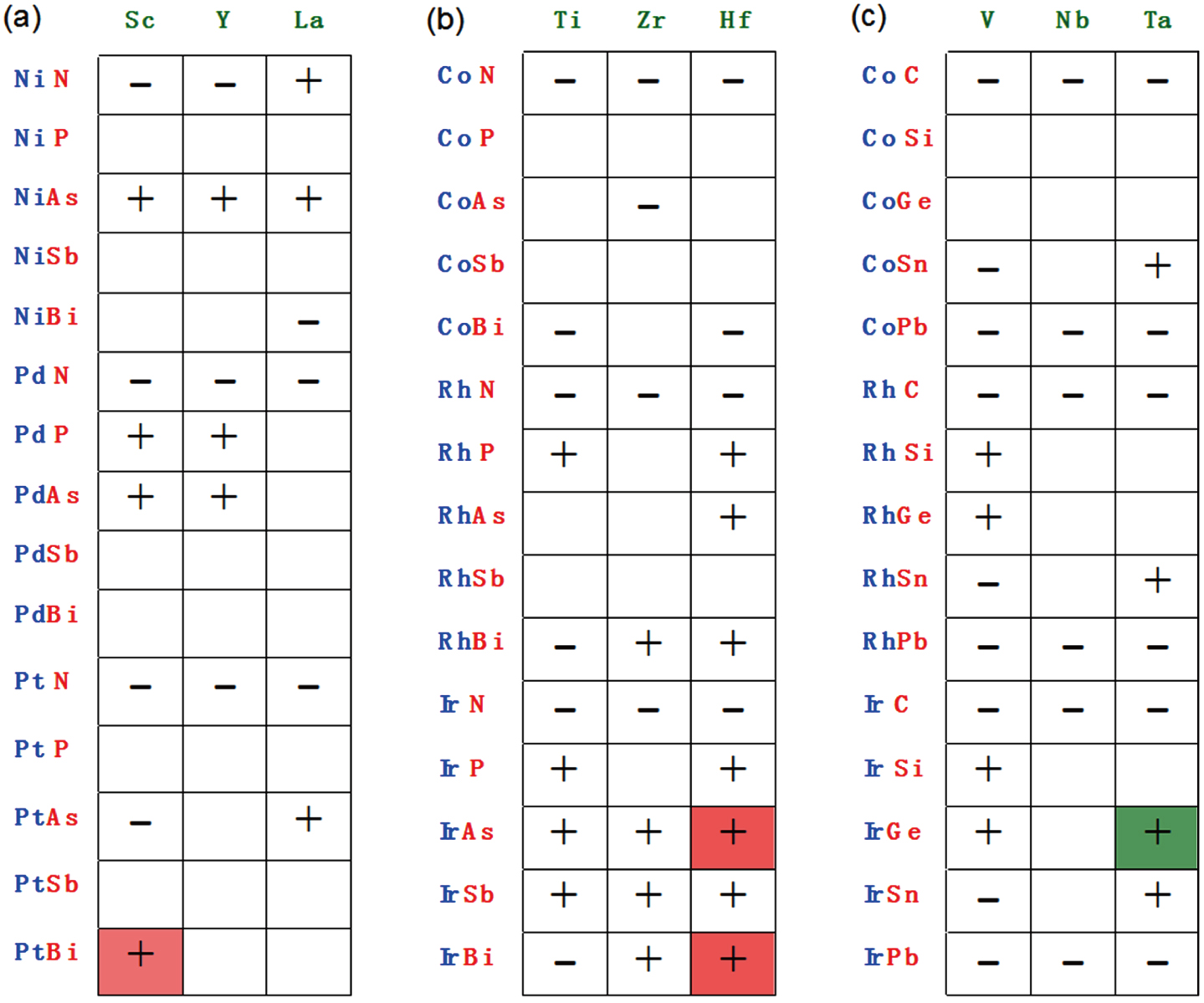 | Fig. 5. (color online) ABX compounds with 18-valence electrons. Elements A are in green, B in blue and X in red. Check mark, previously reported compounds; plus sign, unreported and predicted here to be stable; minus sign, unreported and predicted here to be unstable. Green background indicates the predicted p-type transparent conductor; red background indicates the predicted topological semimetals.[84] |
A number of ABX half-Heusler materials were found to be topological semimetals[26–29] analogous to HgTe including ScPtBi (with 18 valence electrons) that was a hypothetical half-Heusler structure considered in Ref. [26]. It is confirmed in Ref. [84] that ScPtBi is indeed thermodynamically stable with a cubic half-Heusler structure. Furthermore, two new topological semimetals (HfIrAs and HfIrBi) were predicted in Ref. [84] (see Fig.
 | Fig. 6. (color online) Topological band characters of predicted ABX semiconductors and semimetals (Figure adapted from Ref. [84]). |
The spectroscopic limited maximum efficiency (SLME)[95] for photovoltaic (PV) applications of the predicted new ABX compounds[76] were calculated based on GW approximation for the electron’s self-energy.[96] Dozens of high SLME (> 20%) thin-film (500 nm) solar cell absorber materials (e.g., CuCaN, CuNaS, NaMgBi, KYPb, etc.) were predicted.[76]
The existing 18-electron ABX compounds and their alloys are widely used in thermoelectric devices.[21–25]
Many of the predicted ABX compounds could be candidate thermoelectric materials, e.g., high thermopower (−153.9 mV·K−1) and power factor (5.2 μW·cm−1·K−2) was found for the predicted and experimentally confirmed compound ZrNiPb,[84] whose neighboring compound ZrNiSn has already been widely studied for thermoelectric applications[21–25] (Figure
 | Fig. 7. (color online) Formation energy of the dominant defects versus parametric Fermi level in ZrNiSn from hybrid functional calculations. Main panel: positively charged electron–donor defects shown in red and negatively charged electron–acceptor defects shown in blue; their charge states denoted in numbers and their charge transition levels shown in open circles. The Fermi level, VBM and CBM variables are denoted by EF, EV, and EC, respectively. The inset shows the allowed chemical stability region, whereas the red circle shows the specific chemical condition used for the current formation energy versus EF calculations. The small vertical arrows indicate the position of the equilibrium Fermi level at growth condition of 850 °C (Figure adapted from Ref. [91]). |
A number of candidate transparent conductors were identified via materials design in the 18-electron ABX family.[32] These 18-electron ABX (e.g., ZrIrSb, TaIrGe, and TaIrSn) are formed by heavy metals, whereas have wide band gaps induced by strong hybridization between the d orbitals of the two transition metals (e.g., Ta and Ir).[32] Focusing our study on TaIrGe suggests that it is a transparent material with predicted low-concentration of intrinsic p-type carriers induced by the Ge on Ta anti-site defects, thus a potential p-type transparent conductor.[32] Furthermore, it is found that the valence band maximum state of TaIrGe is an anti-bonding state and is delocalized along the empty interstitial channels (in between the Ta–Ir and the Ta–Ge atoms), avoiding the ionic sites that consequently have but a low probability to scatter the mobile carriers. Subsequent experimental study confirmed the theoretically predicted crystal structure, optical transparency and low concentration of holes, thus the p-type transparent conductor functionality in TaIrGe. Significantly, it is discovered in experiments that TaIrGe has very high room temperature (RT) hole mobility (2730 cm2 ·V−1·s−1),[32] higher than the previously reported RT hole mobility of Ge (1900 cm2·V−1·s−1).[97]
In the MgSrSi-type crystal structure (Pnma), there are one-dimensional (1D) Mg–Si ribbons embedded in the three-dimensional (3D) matrix of Sr.
Figure
 | Fig. 8. (color online) Crystal structure of RbCuTe[35] in the MgSrSi-type structure. Green sphere: Rb. Red sphere: Cu. Blue sphere: Te. |
Theoretical design of stable multinary functional materials could lead to the finding of interesting physical properties as well as technologically critical materials. We reviewed the rational substitution approaches for the design of multinary compounds and the high-throughput prediction of new multinary compounds, with their applications in the most succinct multinary family of ABX half-Heusler materials. The new functionalities of the predicted ABX materials were also discussed briefly. Many of the new ABX compounds were realized in experiments that confirmed the predicted crystal structures and physical properties.
The prediction of stable compounds at zero temperature is much faster and more straightforward than the anticipation of high-T phases. However, high-T phases, especially the RT structures, if different than the 0-K phases, are much more important than the latter for both technological application and scientific study. The methodologies and computational techniques for predicting material structures that are stable at nonzero temperature with comparable speed and confidence as the prediction of 0-K phases are crucial for the future high-throughput study of realistic functional materials for near-RT applications.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] |


