† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 41501240, 41530855, 41501241, and 41877026), the Natural Science Foundation of Chongqing CSTC (Grant No. cstc2018jcyjAX0318), and the Fundamental Research Funds for the Central Universities, China (Grant No. XDJK2017B029).
Surface potential is an important parameter related to the physical and chemical properties of charged particles. A simple analytical model for the estimation of surface potential is established based on the Poisson–Boltzmann theory with the consideration of the dielectric decrement in mixed electrolyte. The analytical relationships between surface potential and charge density are derived in different mixed electrolytes with monovalent and bivalent ions. The dielectric decrease on the charged surface strongly affects the surface potential at a high charge density with different ion strengths and concentration ratios of counter-ions. The surface potential based on the Gouy–Chapman model is underestimated because of the dielectric decrement on the surface. The diffuse layer can be regarded as a continuous uniform medium only when the surface charge density is lower than 0.3 C·m−2. However, the surface charge densities of many materials in practical applications are higher than 0.3 C·m−2. The new model for the estimation of surface potential can return to the results obtained based on the Gouy–Chapman model at a low charge density. Therefore, it is implied that the established model that considers the dielectric decrement is valid and widely applicable.
Surface potential is an important parameter of nano-colloidal particles. It determines many ion–surface and surface–surface interactions, such as ion adsorption and transport near the surface,[1–3] interparticle force,[4] aggregate stability[5] and deposition phenomena.[6] Therefore, the estimation of surface potential is a significant issue in colloidal and interfacial chemistry. However, an important physical factor, dielectric decrement at the solid–liquid interface, has been neglected in theories for the estimation of surface potential.
The theories and methods of estimating the surface potential have been proposed based on the double-layer theory,[7–13] the second harmonic generation method,[14,15] x-ray photoelectron spectroscopy method,[16] and replacement by zeta potential.[17] The double-layer[7–9] and second harmonic generation[14,15] methods are mainly based on the Gouy–Chapman (GC) model and density functional theory.[10,11] The hydration repulsion between particles is taken into account in the experimental method based on x-ray photoelectron spectroscopy.[16] The surface potential is usually replaced by the zeta potential that only depends on the magnitude of the shear interface charges. In this study, the surface potential is the potential at the original plane of the diffuse layer or Stern plane, and the shear plane is far from Stern plane[17,18] so it cannot be used as a substitute.
A strong electric field, up to hundred millions volt per meter, exists near a charged surface.[2] The electric field influences the water molecules at the interface, which can significantly reduce the dielectric constant of the medium.[19] The lower dielectric permittivity in this strong electrostatic field will further enhance the complexity of the charged ions into neutral species.[20,21] In predecessors’ methods to measure the surface potential,[22,23] the dielectric decrement was neglected and the surface potential was thus inaccurately estimated.
Furthermore, mixed electrolyte solutions, rather than a single-electrolyte solution, are often encountered in practical applications. Zhao et al. provided a concise description of the GC theory for NaCl/CaCl2 mixtures,[24] which is one of the electrolyte mixtures with monovalent and divalent ions (co-ions and counter-ions). In fact, the interfacial behaviors described by Poisson–Boltzmann (PB) theory depend on the electrolyte composition with different ionic species. However, a simple analytical method of estimating the surface potential in mixed electrolytes considering the dielectric decrement should be established to conveniently apply the PB theory. A theory that more accurately describes the surface potential would provide us with a much more in-depth understanding and a more rational approach to investigating the interfacial behaviors.
The principles for the estimation of the surface potential in mixed electrolytes were proposed in our previous study;[25] nevertheless, the effects of the dielectric decrement on surface potential were neglected. Therefore, an analytical method to estimate the surface potential by considering dielectric decrement is established, and the effects of the dielectric decrement on the surface potential are investigated in this study.
According to the PB equation and the definition of the electric field E = dφ/dx at boundary x → ∞, E = 0, and φ = 0, and at the Stern plane x → 0, E = E0 and φ = φ0, one obtains
Equation (
When the dielectric decrement is neglected, Eq. (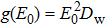

In this study, we select a dielectric function:
Substitution of Eq. (
Combining Eqs. (
Although Eq. (
For 1:1 (AB) single electrolytes, the valence ions A and B are ZA = 1 and ZB = −1, respectively, and their ion concentrations are related by fB = fA. Equation (
For 1:1+1:1 ( AB + A′B’) mixed electrolytes, the valence of ions A and A′, and B and B’ are ZA = ZA′ = 1 and ZB = ZB′ = −1, and their ion concentrations are fB = fA and fB′ = fA′. Equation (
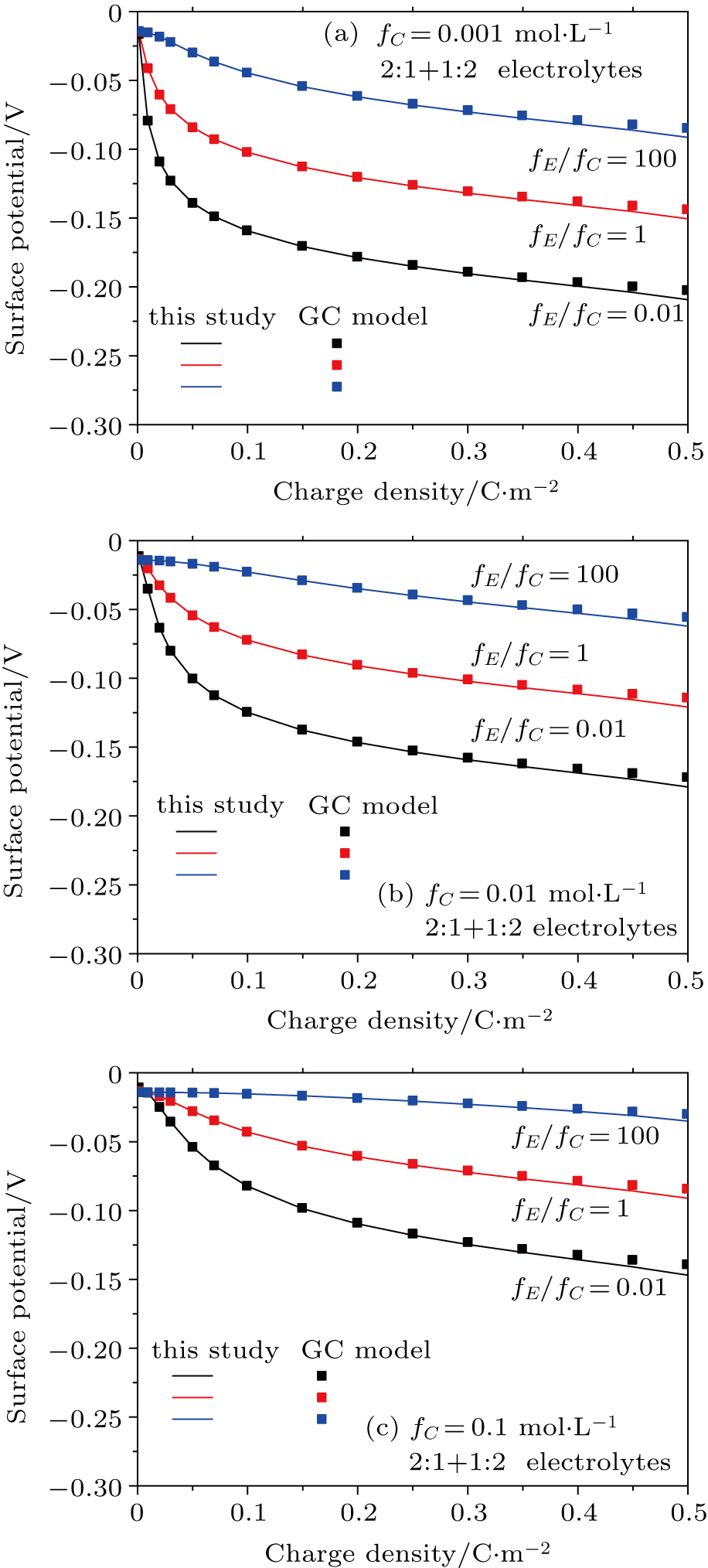
For 2:1 + 1:2 ( EM2 + C2D) mixed electrolytes, the valence of ions E, M, C, and D are ZE = 2, ZM = −1, ZC = 1, and ZD = −2, respectively, and their ion concentrations are related by 2fE = fM and fC = 2fD. Equation (
For 2:2 + 1:2 (EM + C2D) mixed electrolytes, the valence of ions E, M, C, and D are ZE = 2, ZM = −2, ZC = 1, ZD = −2, respectively, and their ion concentrations are related by fE = fM and fC = 2fD. Equation (
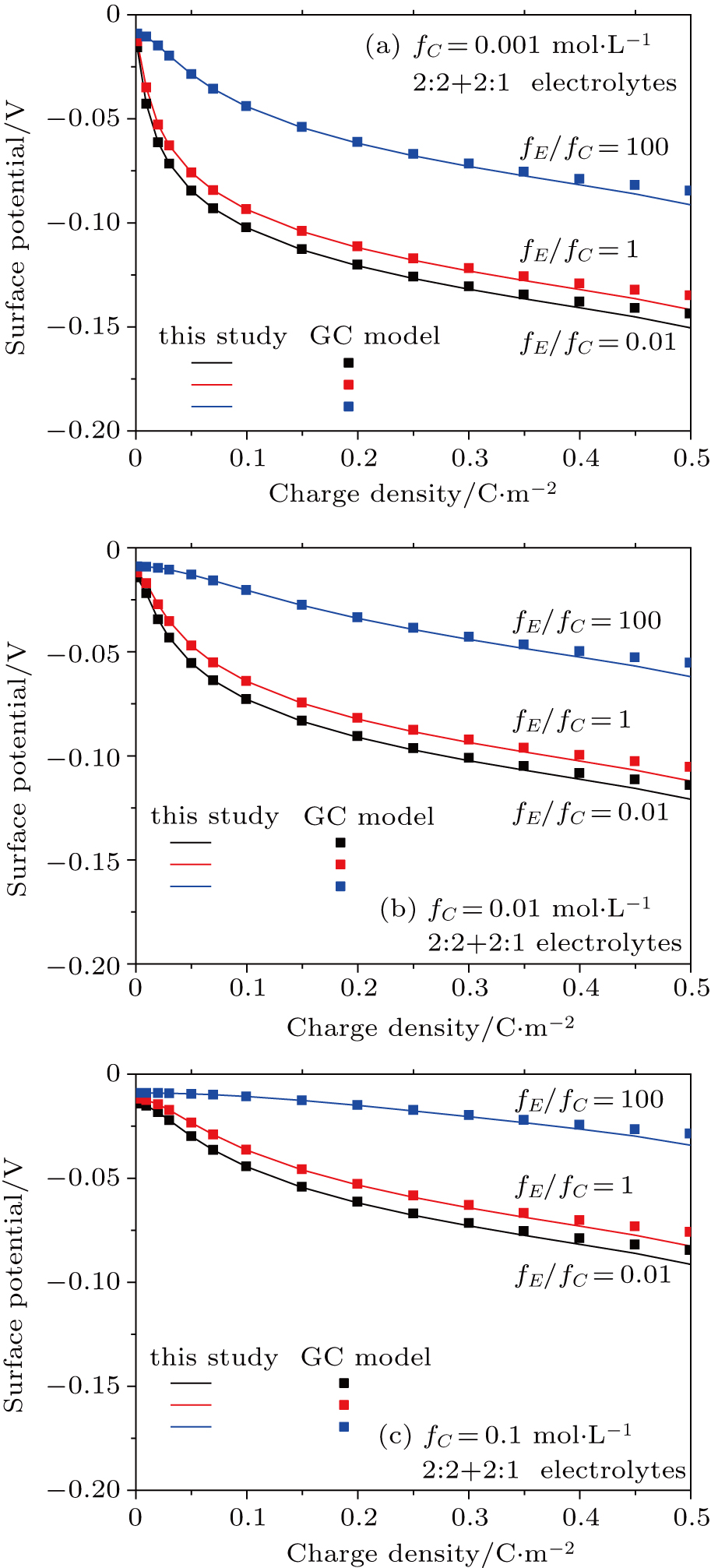
For a 2:2 + 2:1 (EM + CD2) mixed electrolyte, the valence of ions E, M, C, and D are ZE = 2, ZM = −2, ZC = 2 and ZD = −1, and the ion concentrations are fE = fM and 2fC = fD. Equation (
Based on the distribution of electric field in the diffuse layer, the dielectric decrement in the double layer can be approximatively estimated by using Eq. (
The potential distribution in the 1:1 electrolyte is[29]

Thus the electric field E = dφ/dx, specifically
The surface potential in Eq. (
 | Fig. 1. Dielectric constant as a function of (a) surface charge density in an inhomogeneous dielectric medium and (b) distance from charged surface in 0.001 mol·L−1 of a 1:1 electrolyte solution. |
 | Fig. 2. (color online) Comparison between surface potential and zeta potential of montmorillonite with charge density of 0.1129 C·m−2 in KNO3 electrolyte solutions. Data were cited from our previous study.[18] |
Theoretically, the electric field in a double layer depends on the salt concentration, because the thickness of a double layer is determined by electrolyte concentration.[18] Gavish et al. provided a model of dielectric properties as a function of salt concentration with considering the electric field created by ions.[30] In the present study, the correlation between ions is neglected and the electric field is generated by the surface charges of nano-colloidal particles.
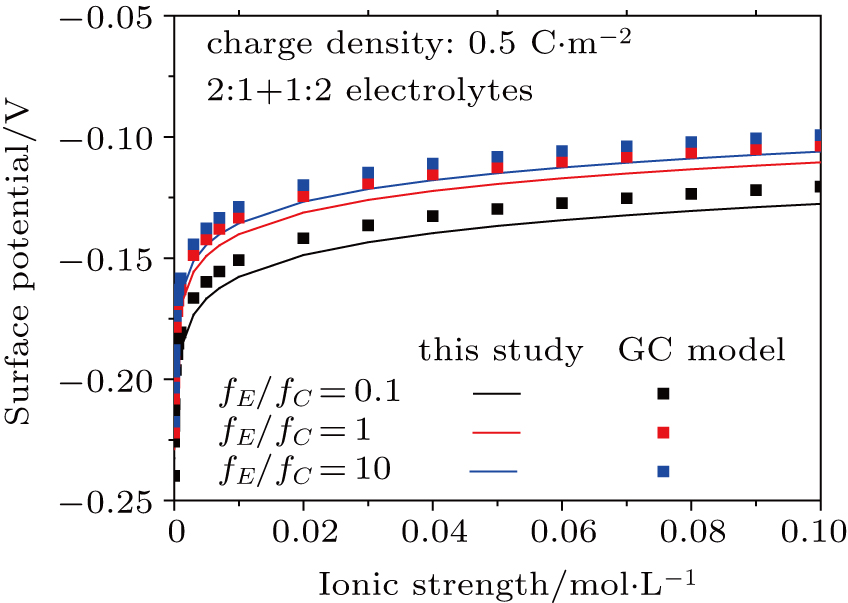
The surface potential is usually replaced by the zeta potential.[31,32] Based on the theoretical calculation of Eq. (
Based on the theoretical calculation of Eqs. (
The surface potential increases with charge density increasing (Fig.
Based on the theoretical calculation of Eqs. (
The results for 2:2 + 1:2 electrolytes shown in Figs.
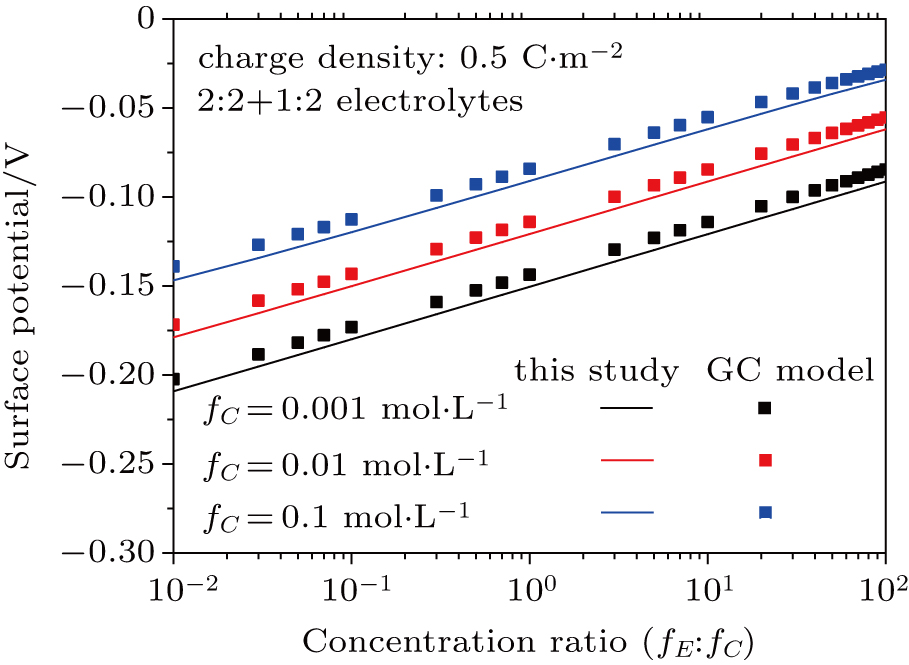
Based on the theoretical calculations of Eqs. (
The trends in 2:2 + 2:1 electrolytes shown in Figs.
It is worth mentioning that only the ion–surface Coulomb interaction is considered in the present study. Based on the theory established in this article, the other factors regarded as the origins of Hofmeister effects, such as ion volume, dispersion and induction effects, will be taken into account in the ion–surface interactions. Combining the dielectric decrement with these factors, a more reliable theory for the estimation of surface potential will be established in subsequent studies. Furthermore, divalent ions show the evidence of specific adsorption into a Stern layer and hence the existence of an isoelectric point.[34] The charge states of variable charge surfaces can be changed due to specific adsorption, thus the surface potential can be changed.[35] In the Stern model the concept of a specific adsorption potential was introduced.[36] In the following studies in this series, the use of an extended model for conditions where specific adsorption potential takes place will be demonstrated.
The principles of surface potential evaluation considering the dielectric decrement in mixed electrolyte solutions are established, and the effects of the dielectric decrement on surface potential are analyzed. A simple and convenient analytical relationship between the surface potential and charge density of nano/colloidal particles is derived. The surface potential can be theoretically calculated as long as the surface charge density of the particles is measured without solving the numerical solution of the PB equation. Dielectric decrement on the charged surface strongly affects the surface potential for a charge density > 0.3 C·m−2 in different ion strengths and concentration ratios of counter-ions. The hypothesis of a homogeneous medium in the GC model obviously underestimates the surface potential and overestimates the dielectric properties at the solid–liquid interface. This study provides an approach to estimating the interfacial interactions and surface potential by taking into account the Hofmeister effects, which will be performed in subsequent studies.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] |