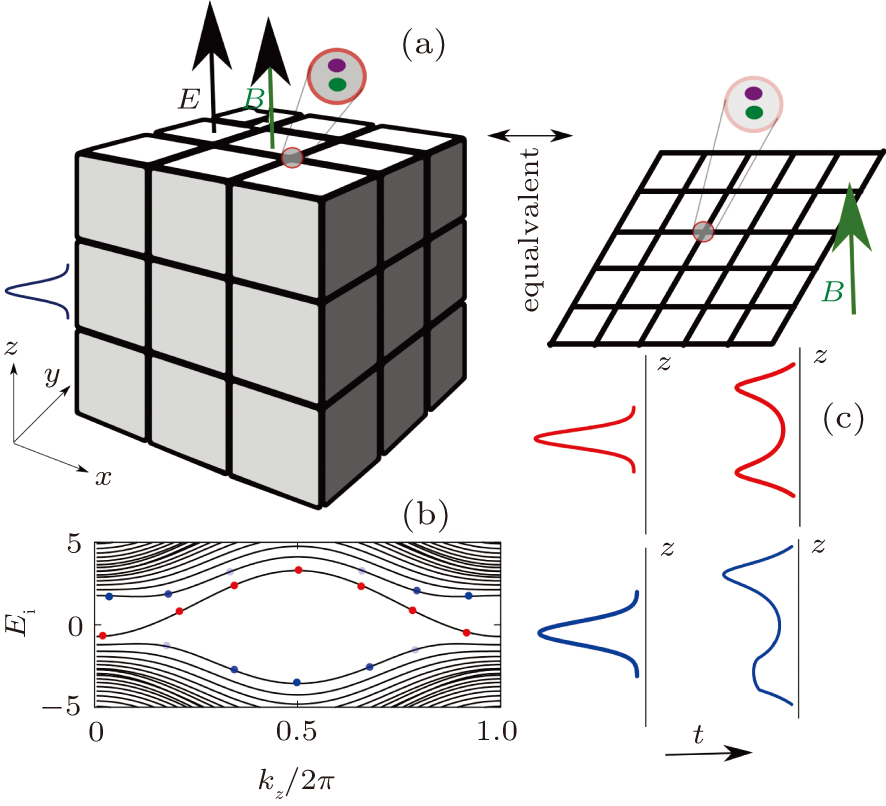
(color online) (a) Left: The 3D cubic lattice described by Eq. (9). Each site has two internal states standing for spin, orbital or sub-lattice degrees of freedom. External electric field E and magnetic field B are applied in the z direction. Right: The 2D square lattice in Eq. (11). This lattice also has two internal degrees of freedom on each site. A magnetic field B is applied perpendicular to the plane. The Hamiltonians of the two models are the same after extending the SD in time in the 2D model. (b) The spectrum of the 3D lattice when BS = 2π/21 and E = 0, where S is the area of one plaquette on the horizontal plane. The dots, whose color depths are standing for the weights |〈ϕ_i(k_z) |ψ(t = 0)〉|, show the initial wave packets |ψ(t = 0)〉 projected on the Landau band eigenstates |ϕ_i(k_z)〉 with red and blue colors distinguishing the two cases. Here i is the index of the Landau levels and the momenta(defined on the magnetic unit cell) on the xy plane are taken as k_x = k_y = 0 implicitly for both the wave packets and the eigenstates. (c) In the first case(red), the wave packet will always be symmetric with respect to the z = 0 plane. But in the second case (blue), the shape of the wave packet should be asymmetric after evolution.