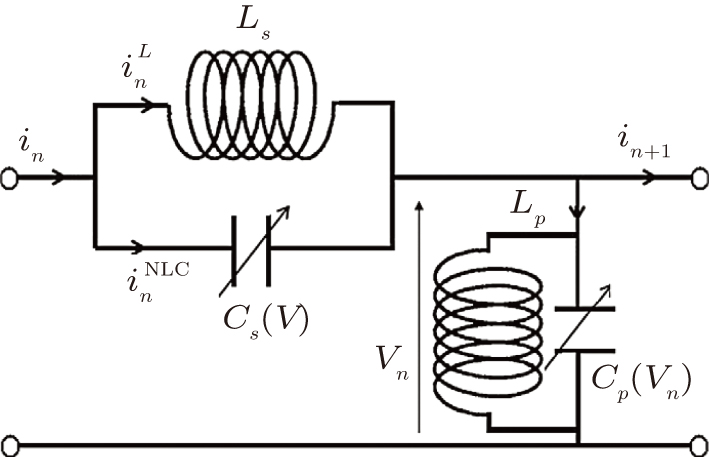
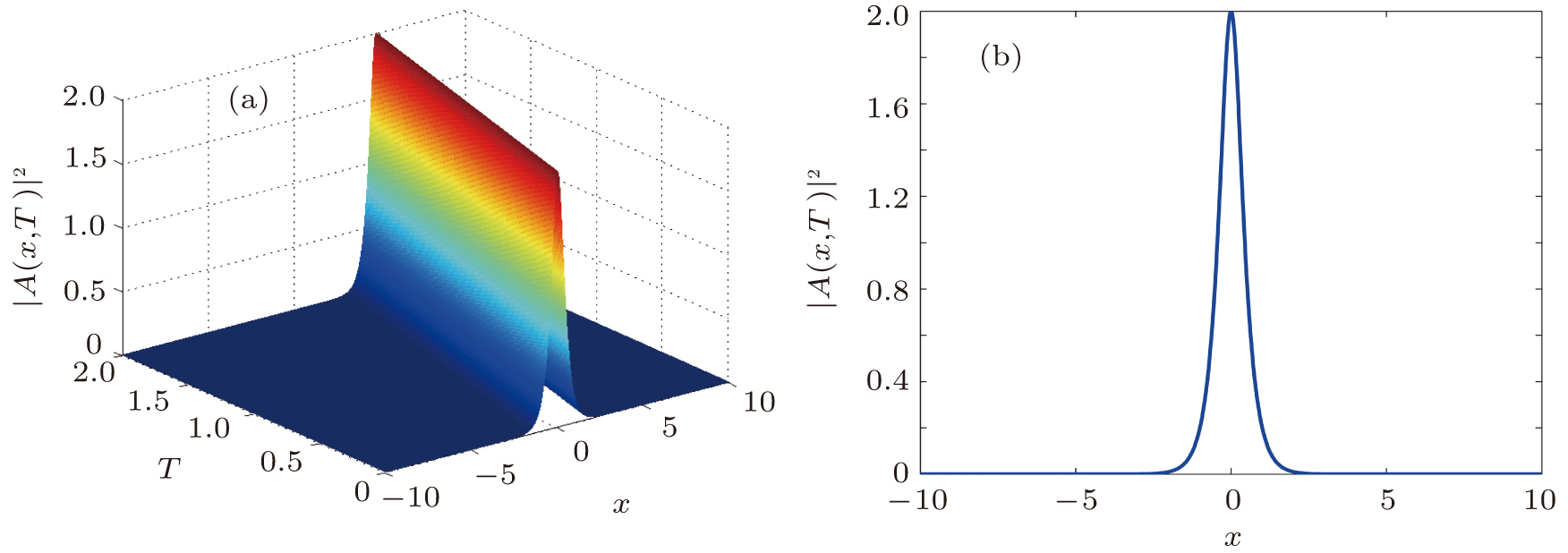
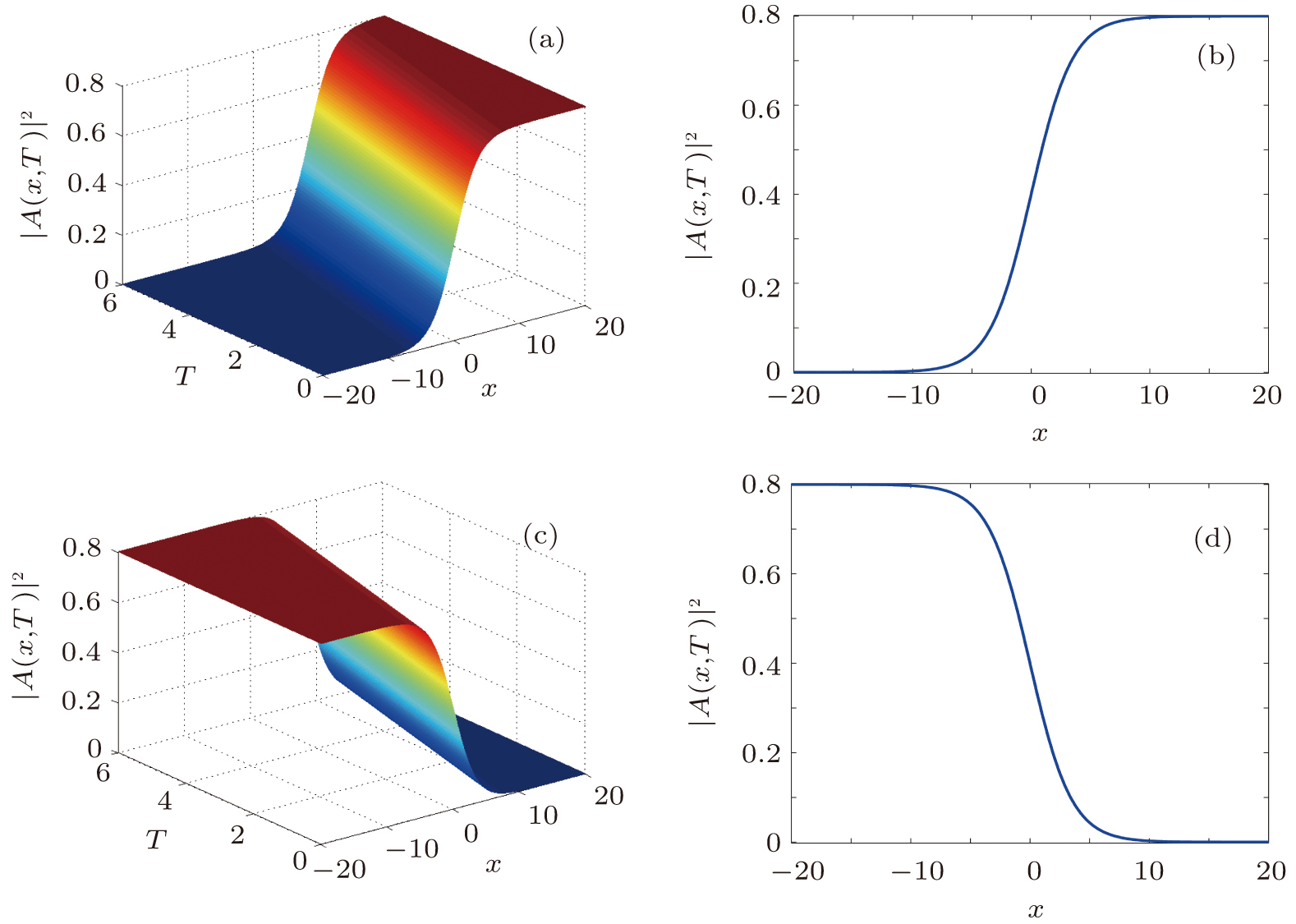
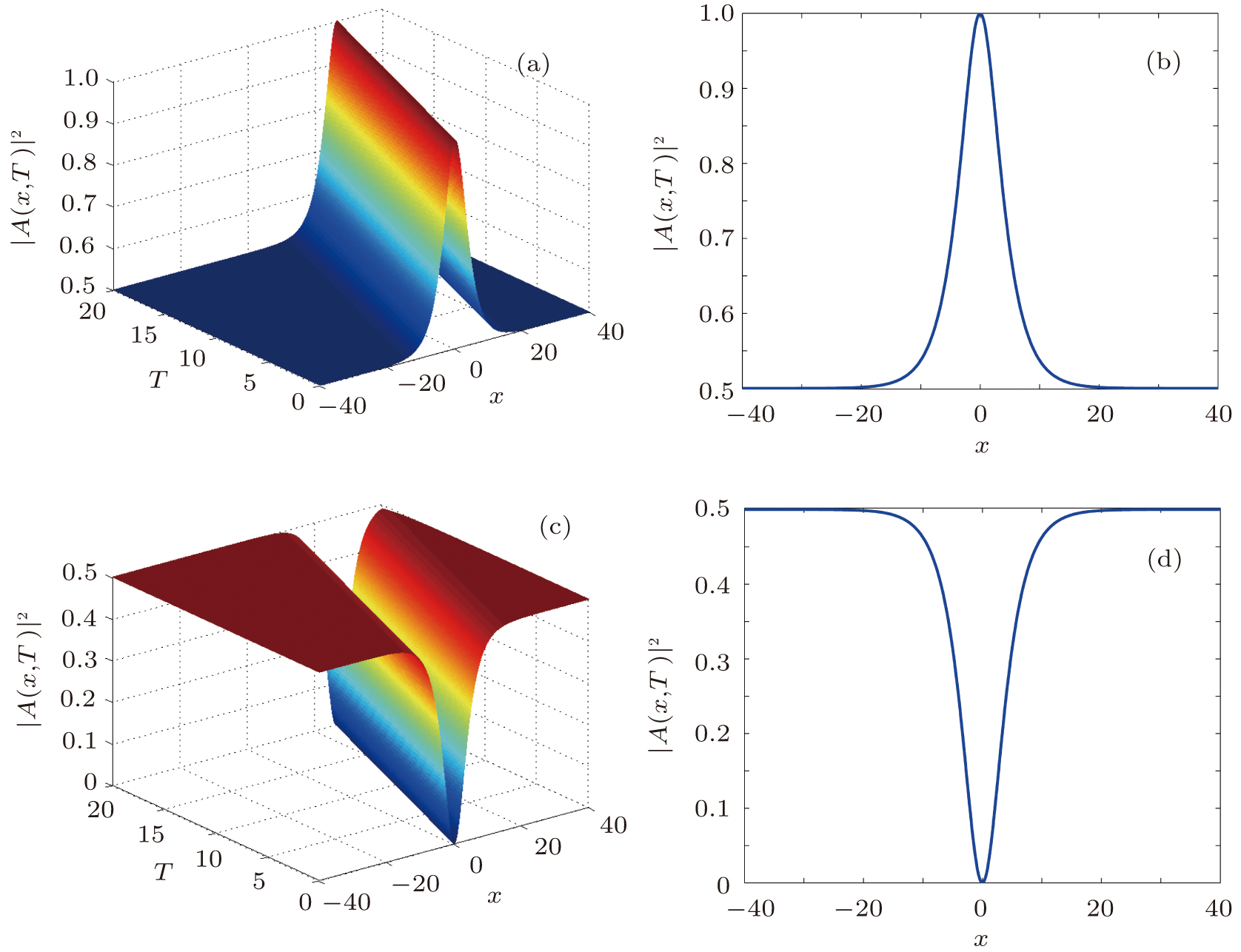
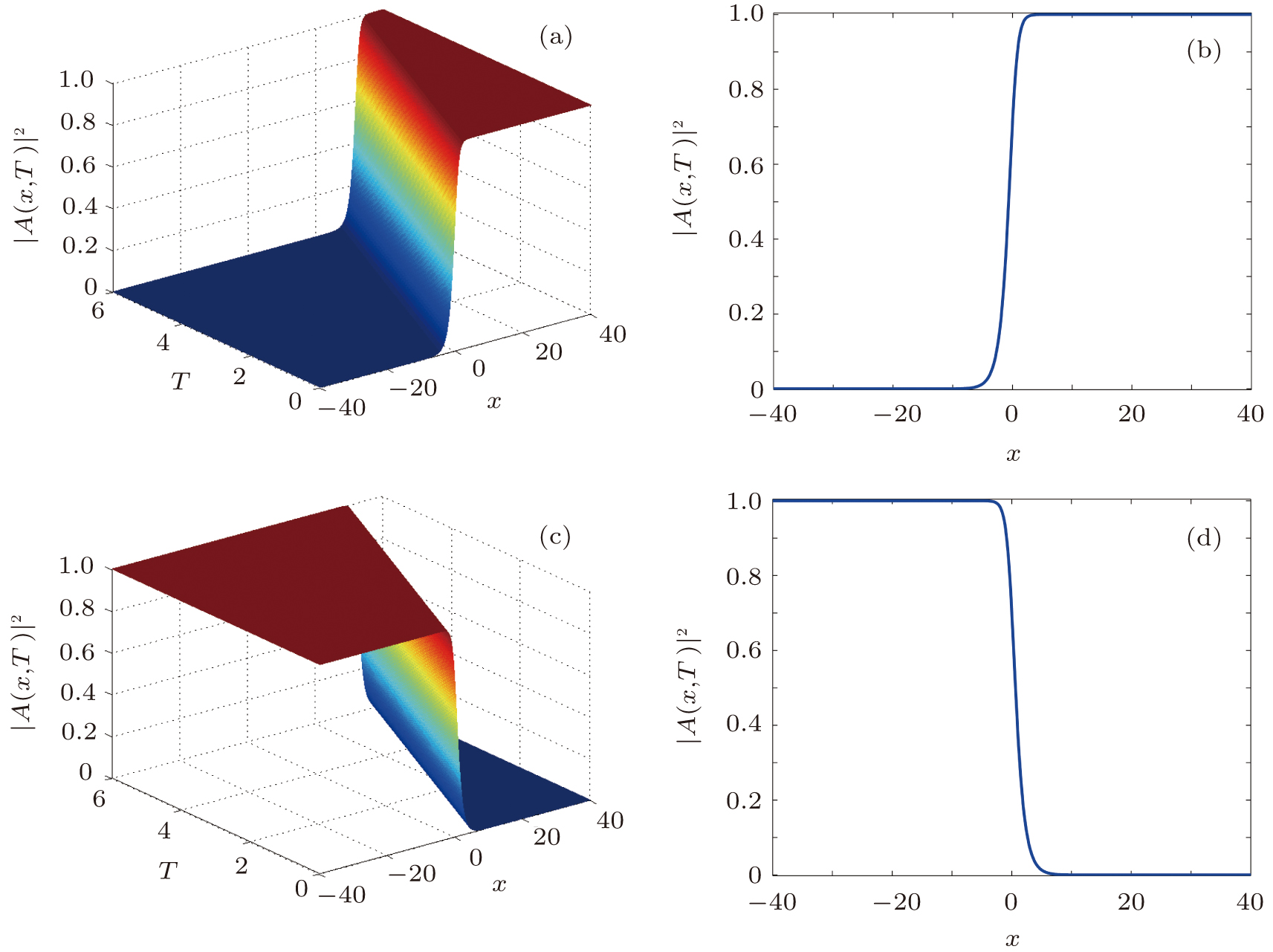
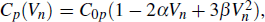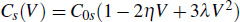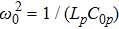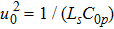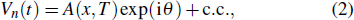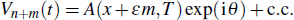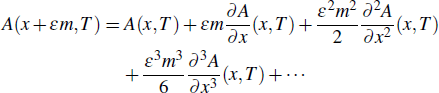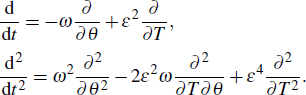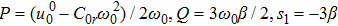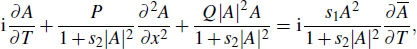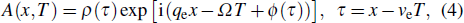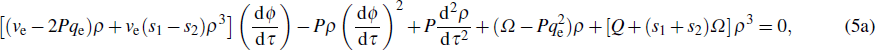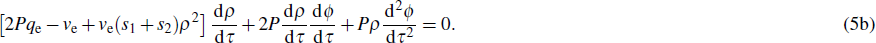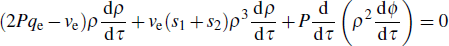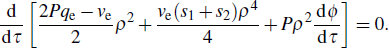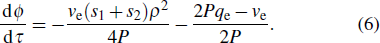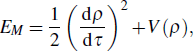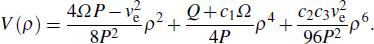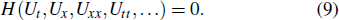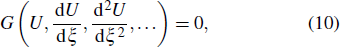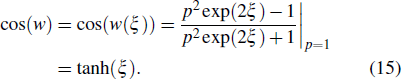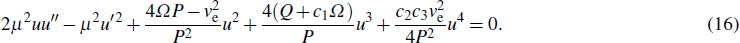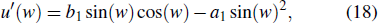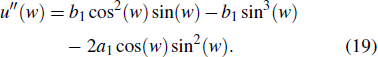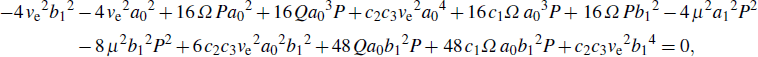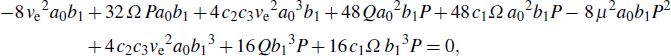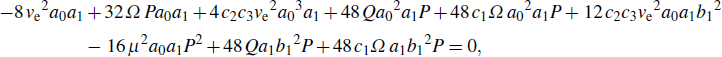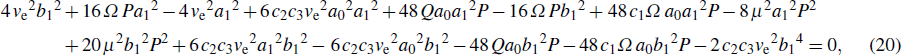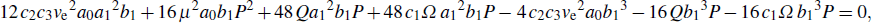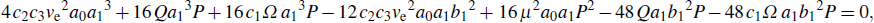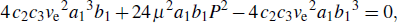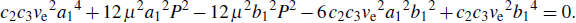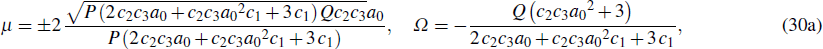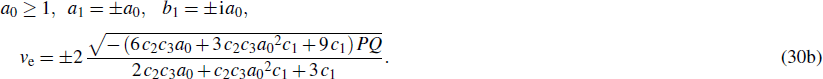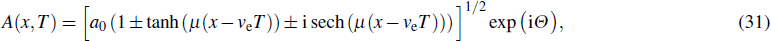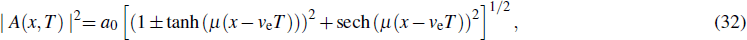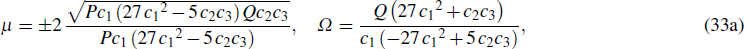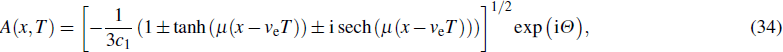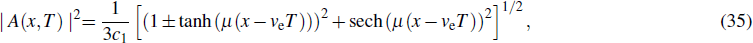1. IntroductionNonlinear equations are widely used as models to describe many important dynamical phenomena in various fields of sciences, particularly in nonlinear optics,[1–4] in plasma physics,[5,6] in biophysics,[7] in Bose–Einstein condensates,[8] in atomic chain,[9,10] in Fermi–Pasta–Ulam lattice,[11,12] in crystals,[13–16] and in discrete electrical transmission lines.[17–24] Among these equations, the famous nonlinear Schrödinger (NLS) equation is usually derived from fundamental principles as a primary approximation. As such, its suitability for the accurate description of the phenomena of interest in these fields can be limited. This has aroused the interest in investigation approaches that relax some of the assumptions that are usually considered in a first approximation. Such approaches often lead to generalized forms of the nonlinear Schrödinger equation rather than the standard one. Consider for instance a discrete nonlinear electrical transmission line (DNLTL) that consists of a number of identical LC blocks connected in sequence one to the other. Each block, whose model is presented in Fig. 1, contains two linear inductors Ls and Lp of which one is in the series branch and the other in shunt branch, and a bias-dependent capacitor Cp responsible for the nonlinearity.
We assume that the capacitance–voltage relationships are approximated by
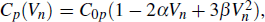 , and
, and
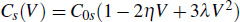 respectively for the nonlinear capacitor Cp(Vn) in the parallel branch and for the one in the series branch, Cs(V). Thus, C0p and C0s are the respective limiting values of these capacitances when the voltages across them are infinitesimally small. α and β, and similarly η and λ, represent respectively the quadratic and cubic coefficients of nonlinearity.
respectively for the nonlinear capacitor Cp(Vn) in the parallel branch and for the one in the series branch, Cs(V). Thus, C0p and C0s are the respective limiting values of these capacitances when the voltages across them are infinitesimally small. α and β, and similarly η and λ, represent respectively the quadratic and cubic coefficients of nonlinearity.
Applying Kirchhoff laws to this circuit leads to the following set of differential equations governing the dynamics of signals in the network[15]
with
n being the total number of blocks. Here,
C0r =
C0s/
C0p is a dimensionless constat while
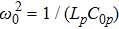
and
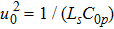
are characteristic frequencies of the system. Equation (
1) has been used to investigate analytically and numerically the peak solitary wave and the modulational instability phenomenon in network.
[26] Similarly, it has been used also to describe the dynamics of modulated waves in the specific case of the linear capacitor
Cs in the series branch, that is, for
η =
λ = 0.
[18,27,28] Other special cases of this equation abound in the study of nonlinear discrete electrical transmission lines.
[21,29]A basic approximation that is commonly made in investigating equations of this type consists in taking their solutions in the form A0exp(i(kn–ωt)) while assuming A0 to be infinitesimally small. Such solutions are characterized the so-called linear dispersion relation, given in our case by
where
ω (rad/s) and
k (rad/cell) are, respectively, the angular frequency and wave number. The graph of the above relation, shown in Fig.
2, presents a lower cutoff mode frequency when
k = 0 and an upper cutoff frequency when
k =
π; which indicates that the network is a bandpass waveguide.
Focusing our attention on waves with frequencies approaching the lower cutoff frequency of the lattice but with amplitude of arbitrary magnitude, we look for a solution of Eq. (1) in the form
where “c.c.” stands for complex conjugate,
θ = −
ωt is the phase variable,
x =
εn and
T =
ε2t with a dimensionless parameter
ε are introduced to account for the slow temporal and spatial variations of the amplitude induced by the mutual coupling between the oscillators. It is obvious from Eq. (
3) that the voltage at any site shifted by an integer
m from a reference site
n is given by
In order to reduce the mathematical intractability of the manipulations involved in the analysis, we assume that 0 ˂
ε ≪ 1 so that Taylor expansions of the following form
are warranted. Here the specific values
m = 1 and
m = −1 are relevant for Eq. (
1). The use of the variables
θ,
x, and
T also implies that the time derivative operators are transformed according to
Considering the above relations, the dynamics of the envelop
A(
x,
T) is governed by the following nonlinear partial differential
with
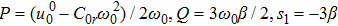
, and
s2 = −6
β.
This equation differs from the classical NLS equation by the two terms of cubic nonlinearity in its right-hand-side. It is worth to observe that these terms involve derivatives with respect to the variable attached with the first order derivative in the standard NLS equation. Although the s2-term can be considered to be common in NLS type equations with saturable nonlinearity, the s1-term as well as the full right-hand-side of Eq. (3) have, to the best of our knowledge, rarely been considered. Equation (3) has been derived above as governing the transmission of modulated signals with carrier frequency in the lower gap of the spectrum of this system. However, the legendary universality of NLS type equations makes it legitimate to expect that its applications can extend beyond discrete electrical transmission line. For instance, this equation may also be written in the form
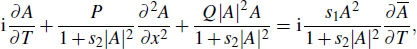 | |
which shows that it is a generalized NLS equation with saturable type nonlinearities. Accordingly, waves propagation in media modeled by such nonlinearities,
[30–33] including metamaterials in particular, can possibly be investigated experimentally using basic nonlinear discrete electrical transmission lines.
[34] This further motivates the interest in the solutions of Eq. (
3). In the literature, these solutions exist on several forms
[4,8,35–42] and are very significant for the description of the phenomena in diverse fields of Physics and Engineering.
Our investigations in this work then aim to determine exact and explicit analytical solutions to this new model of NLS equation. To this end, our paper is organized as follows. The next section begins with the reduction of the extended NLS equation to a single nonlinear ordinary differential equation (ODE). Sine–Gordon expansion-method, which is among the most powerful and effective method devised by mathematicians and physicists to find exact solutions of ODEs is then briefly outlined. In Section 3, the exact solitary wave solutions of this last equation will be given. The last section will be devoted to the conclusion.
2. The methods2.1. ODE equationOver the past several decades, many research works have focused on techniques for solving partial differential equations (PDEs). A first step in most of these techniques consists in reducing the PDEs in consideration into ODEs. In this view, we are interested in this paper by the class of solutions of Eq. (3) which can be represented by
where
qe,
qe, and
Ω are real constants to be determined as part of solutions while
ρ and
ϕ and real-valued functions of a single variable. Substituting Eq. (
4) into Eq. (
3) and separating the real and imaginary part leads to the following system of coupled nonlinear ODEs:
It is easy to verify that equation (
5b) becomes an exact differential if multiplied by
ρ. Doing so leads in effect to
or
It is then clear that
where
C0 is an arbitrary constant. This last equation is a first integral of Eq. (
5b). It can be easily solved for d
ϕ/d
τ. Considering the particular case where
C0 = 0, we obtain
For simplicity, we fix the
qe so that the derivative of the phase
ϕ(
τ) is proportional to
ρ2. Thus
By introducing Eq. (
6) into Eq. (
5a) while accounting for Eq. (
7), we obtain the following single nonlinear ODE which governs the real amplitude of the wave:
with
c1 =
s1 −
s2,
c2 =
s1 +
s2, and
c3 = 3
s2 − 5
s1. Equation (
8) is the celebrated cubic–quintic Duffing oscillator equation whose periodic solutions have been the focus of several research papers.
[43–45] It is worth to notice that the quintic term in this equation is induced by the two nonlinear temporal terms of Eq. (
3), though they are only of cubic order nonlinearity.
The next step after transforming the PDEs into ODEs is the effective determination of solutions to the latter. A first approach toward this goal for our problem is a direct integration from the first integral
which underlines the analogy of Eq. (
8) with the Newtonian equation of motion of a point particle of unit mass. Here, the wave amplitude
ρ(
τ) plays the same role as the relative displacement of the particle; which moves freely in the following non-harmonic potential
This approach leads to an improper integral which contains a square root of a six-degree polynomial in the denominator
[20] and so is quite difficult to evaluate.
The alternative approach preferred herein rely on the variety of methods available in the literature to deal with this task and which avoid the direct integration. Examples are the (G′/G)-expansion method,[46,47] the exp-expansion method,[48] the extended F-expansion method,[49] the bifurcation method of dynamical system,[50,51] the Jacobi elliptic function rational expansion method,[52] the tanh-function method,[53,54] the tan-expansion method,[55] the transformed rational function method,[56,57] the semi-inverse variational principle,[58] the Hirota bilinear method,[59–62] the variable coefficient Jacobian elliptic function method,[63] the sine-Gordon expansion approach,[64–67] and others. For our problem, the sine-Gordon expansion-method has revealed to be very effective. An important advantage of this techniques is that the computations involved can be systematically performed by a computer algebra system such as Maple or Mathematica. Below, it is briefly reviewed and used later to find various forms of solution to Eq. (8).
2.2. The sine-Gordon expansion-methodIn this subsection we present the sine-Gordon expansion method which will later be utilized to investigate the solitary waves that can propagate through our discrete electric transmission line. This method is based on sine-Gordon equation and the traveling wave transformation.[68–70]
In fact, consider a nonlinear partial differential equations (NLPDEs) with two independent variables x and t,
In general, the left-hand side of Eq. (
9) is a polynomial in
U and its various derivatives. Assume that
U(
x,
t) =
U(
ξ),
ξ =
kx −
υct, where
k and
υc are constants to be determined later. Then equation (
9) is reduced to an ordinary differential equation
where
G is a polynomial of
U and its various derivatives. We consider that the sought solution can be expressed as follows:
According to Refs. [
65]–[
67], equation (
11) can be rewritten as
where the function
w(
ξ) =
U(
ξ)/2 satisfies the following relation
Equation (
13) is variables separable. We obtain the following two significant equations upon solving it
The parameter
M is, in most cases, a positive integer that can be determined by considering the homogeneous balance between the highest order derivative and the highest order nonlinear terms appearing in ODE (
10). Collecting and setting the coefficients of terms of the form sin
i(
w)cos
j(
w) to zero yields a system of coupled nonlinear algebraic equations. Solving this system by using Maple gives the values of
ai,
bi,
a0,
k1, and
υc. Finally, substituting these values of Eq. (
11), we obtain the traveling wave solutions to Eq. (
10).